Bộ 10 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 10
5 câu hỏi
1. Xét các phương trình sau:
\({x^2} - \sqrt {5x} + 1 = 0;\) \( - 3{x^2} + 4\sqrt 6 x - 4 = 0;\) \( - 5{x^2} - 4y + 1 = 0;\) \( - {x^2} - \frac{3}{2}x - \frac{1}{2} = 0.\)
a) Trong các phương trình trên, chỉ ra phương trình bậc hai một ẩn và xác định hệ số \(a,b,c\).
b) Giải các phương trình tìm được ở phần a).
2. Giải bài toán sau bằng cách lập phương trình:
Bạn An chia đoạn thẳng \(AB\) dài 10 cm thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn \(AB\) bằng tỉ số giữa đoạn nhỏ với đoạn lớn. Hãy tìm tỉ số ấy.
Cho parabol \(\left( P \right):y = - \frac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):y = \frac{x}{2} - 1\).
a) Trong các điểm \(A\left( { - 2; - 2} \right);B\left( {1; - \frac{1}{2}} \right);C\left( {2;0} \right);D\left( { - 1; - \frac{1}{2}} \right)\), điểm nào thuộc cả \(\left( P \right)\) và \(\left( d \right)\).
b) Tìm trên \(\left( P \right)\) điểm có hoành độ gấp ba lần tung độ.
c) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.
Cho phương trình \({x^2} - 2x + m = 0\) (1) (\(x\) là ẩn số)
a) Giải phương trình (1) khi \(m = 2\).
b) Tìm các giá trị của \(m\) để phương trình (1) có nghiệm.
c) Tìm các giá trị của \(m\) để phương trình (1) có nghiệm \({x_1},{x_2}\) thỏa mãn đẳng thức:
\(x_1^3{x_2} + {x_1}x_2^3 - 2x_1^2x_2^2 = 5\).
1. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {3;\,\,3} \right)\) và \(B\left( { - 3\sqrt 2 ;\,\,0} \right)\) như hình dưới đây.
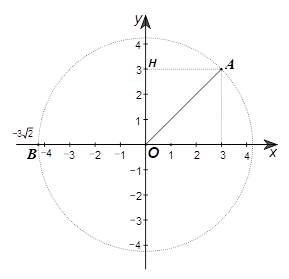
Hỏi phép quay ngược chiều tâm \(O\) biến điểm \(A\) thành điểm \(B\) có góc quay bằng bao nhiêu độ?
2. Cho đường tròn tâm \(O,\) đường kính \(AD.\) Hai dây cung \(AC\) và \(BD\) cắt nhau tại \(E\) \((E\) nằm bên trong đường tròn \(\left( O \right)).\) Vẽ \(EF\) vuông góc với \(AD\) tại \(F.\) Chứng minh rằng:
a) Tứ giác \(ABEF\) nội tiếp.
b) \(FE\) là tia phân giác của \(\widehat {BFC}.\)
c) Điểm \(E\) là tâm đường tròn nội tiếp tam giác \(BCF.\)
Giải phương trình sau: \(\sqrt {x - 2025} + 3\sqrt {x + 6} = 3 + \sqrt {\left( {x - 2025} \right)\left( {x + 6} \right)} \).








