Bộ 10 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 07
5 câu hỏi
1. Xét các phương trình dưới đây:
\({\left( {x - 5} \right)^2} - 11 = 0;\) \( - \frac{3}{5}{x^3} - \frac{7}{2}x = 0;\) \(3{x^2} - 2\sqrt 3 x + 1 = 0;\) \({x^2} - 2y + 5 = 0.\)
a) Trong các phương trình trên, chỉ ra phương trình bậc hai một ẩn và các hệ số \(a,b,c\) của phương trình đó.
b) Giải phương trình tìm được ở phần a).
2. Giải bài toán sau bằng cách lập phương trình:
Một mảnh vườn hình chữ nhật \(ABCD\) có chu vi và diện tích lần lượt là \(70{\rm{\;m}}\) và \(250{\rm{\;}}{{\rm{m}}^2}.\) Người ta chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh \(ADE,\) khu trồng hoa \(BEDF,\) khu thư giãn \(BCF\) với \(BE = DF = 6{\rm{\;m}}\) như mô tả ở hình bên.
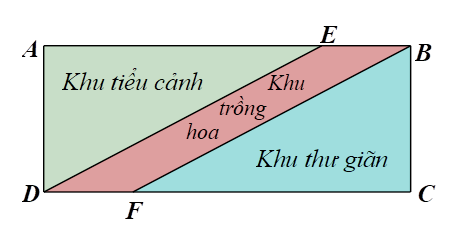
Người chủ vườn đã thuê người trồng hoa ở khu trồng hoa với chi phí là 50 000 đồng/m2. Tính số tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó.
Cho hàm số \(y = a{x^2}{\rm{ }}\left( {a \ne 0} \right)\) có đồ thị hàm số \(\left( P \right)\).
a) Xác định \(a\) biết \(\left( P \right)\) đi qua điểm \(A\left( {1; - 2} \right)\).
Với giá trị \(a\) vừa tìm được ở trên hãy:
b) Vẽ đồ thị \(\left( P \right)\) với \(a\) vừa tìm được.
c) Tìm điểm thuộc \(\left( P \right)\) có hoành độ bằng \(\frac{2}{3}.\)
Cho phương trình \(\left( {2m - 3} \right){x^2} - 2\left( {m - 2} \right)x - 1 = 0\) với \(m\) là tham số.
a) Giải phương trình với \(m = 2.\)
b) Chứng minh rằng với mọi \(m \in \mathbb{R}\), phương trình luôn có nghiệm.
c) Tìm giá trị của \(m\) để phương trình có hai nghiệm phân biệt thỏa mãn \(2{x_1} + 3{x_2} = 5\).
1. Trên mặt phẳng toạ độ \[Oxy\] cho \(A\left( { - 2;\,\, - 2} \right).\) Phép quay thuận chiều \[90^\circ \] tâm \[O\] biến điểm \[A\] thành điểm \[I.\] Khi đó, hãy tìm tọa độ của điểm \(I.\)
2. Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại hai điểm phân biệt \(A,\,\,B.\) Đường thẳng \(AO\) cắt hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) lần lượt tại hai điểm \(C,\,\,E\) (khác điểm \(A).\) Đường thẳng \(AO'\) cắt hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) lần lượt tại hai điểm \(D,\,\,F\) (khác điểm \(A).\) Chứng minh:
a) \(C,\,\,B,\,\,F\) thẳng hàng.
b) Tứ giác \(CDEF\) nội tiếp đường tròn.
c) \(A\) là tâm đường tròn nội tiếp tam giác \(BDE.\)
Giải phương trình sau: \({x^2} - 2x - 1 = \sqrt {\left( {{x^2} + 1} \right)\left( {x + 1} \right)} \).








