Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 7
16 câu hỏi
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\[\frac{5}{x} + 8y = 1\].
\[5xy + 8y = 0\].
\(5x - 8y = 0.\)
\[5\frac{x}{y}--\frac{1}{8}y = 0.\]
Phương trình \[4x - 3y = 2\] nhận cặp số nào sau đây làm nghiệm?
\[\left( {1\,;\,\, - 2} \right)\].
\[\left( {1\,;\,\, - 1} \right)\].
\[\left( {2\,;\,\,2} \right)\].
\(\left( {1\,;\,\,1} \right).\)
Trên mặt phẳng tọa độ \[Oxy,\] cho các điểm \[A\left( { - 1\,;\,\, - 1} \right),{\rm{ }}B\left( {2;3} \right),{\rm{ }}C\left( {5;6\,} \right),{\rm{ }}D\left( {1\,;\,\,2} \right).\] Đường thẳng \[ - 4x + 3y = 1\] đi qua hai điểm nào trong các điểm đã cho?
\[A\] và \[B\].
\[B\] và \[C\].
\[C\] và \[D\].
\[D\] và \[A\].
Cặp số nào sau đây là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}5x + 4y = 1\\3x - 2y = 5\end{array} \right.\]?
\[\left( { - 3\,;\,\,2} \right)\].
\[\left( {1\,;\,\, - 1} \right)\].
\[\left( {3\,;\,\, - 2} \right)\].
\[\left( { - 3\,;\,\, - 2} \right).\]
Điều kiện xác định của phương trình \(\frac{1}{{x + 2}} + 1 = \frac{2}{{x - 1}}\) là
\[x \ne - 2;{\rm{ }}x \ne 1\].
\[x \ne 2;{\rm{ }}x \ne 1\].
\[x \ne - 3;{\rm{ }}x \ne --2\].
\[x \ne 1;{\rm{ }}x \ne - 3\].
Cho \(a + 3 > b + 3\), khi đó ta có:
\(a < b.\)
\( - 3a - 3 > - 3b - 3.\)
\(4a < 4b.\)
\(3a + 1 > 3b.\)
Với ba số \(a,b\) và \(c < 0\), các khẳng định sau khẳng định nào đúng?
Nếu \[a > b\] thì \(ac > bc.\)
Nếu \(a > b\) thì \(\frac{a}{c} > \frac{b}{c}.\)
Nếu \(a > b\) thì \(ac < bc.\)
Nếu \(a > b\) thì \(a + c < b + c.\)
Vế trái của bất phương trình \[ - 15x + 4 \le 0\] là
\[ - 15x + 4\].
\[ - 15x\].
\[ - 15x - 4\].
0.
Cho \(\Delta ABC\) vuông tại \[A,\] có \[AB = 3{\rm{ cm}},{\rm{ }}AC = 4{\rm{ cm}},{\rm{ }}BC = 5{\rm{ cm}}.\] Khi đó \(\sin C\) bằng
\(\frac{3}{5}\).
\(\frac{4}{5}\).
\(\frac{5}{4}\).
\(\frac{5}{3}\).
Tính chiều cao \(AH\) với các số liệu cho trên hình sau. Kết quả nào sau đây là đúng?
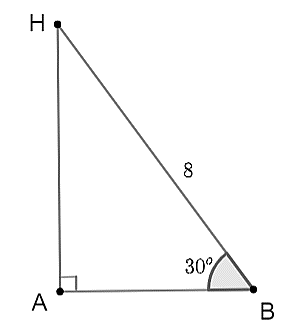
\(AH = 4.\)
\(AH = 2.\)
\(AH = 8.\)
\(AH = 3.\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 10\,\,{\rm{cm}},\,\,\widehat C = 40^\circ .\) Cạnh \(BC\) có độ dài gần nhất với kết quả nào dưới đây?
\(12,45\)cm.
\(15,56\,\,{\rm{cm}}{\rm{.}}\)
\(6,43\,\,{\rm{cm}}{\rm{.}}\)
\(8\)cm.
(1,0 điểm) Giải các hệ phương trình sau:
a) \[\left\{ \begin{array}{l}2x + 5y = 8\\2x - 3y = 0\end{array} \right.\];
b) \[\left\{ \begin{array}{l}2x - 3y = 7\\3x + 2y = 4\end{array} \right..\]
(2,0 điểm) Giải phương trình và bất phương trình sau:
a) \[4x\left( {x - 3} \right) - 3x + 9 = 0\];
b) \(\frac{2}{{x - 3}} - \frac{3}{{x + 3}} = \frac{{3x + 5}}{{{x^2} - 9}}\);
c) \[3\left( {x + 2} \right) \le x - 8\];
d) \(3\left( {x - 2} \right) + 7x \le 4\left( {x + 1} \right) + 14\).
c) \ [3 \ left ({x + 2} \ right) \ le x - 8 \]; d) \ (3 \ left ({x - 2} \ right) + 7x \ le 4 \ left ({x + 1} \ right) + 14 \).
(1,5 điểm) Trong kì thi vào THPT, hai trường A và B có tổng cộng \(500\) học sinh dự thi. Kết quả hai trường đó có \(420\) học sinh trúng tuyển. Trường A có \(80\% \) học sinh trúng tuyển, trường B có \(90\% \) học sinh trúng tuyển. Hỏi mỗi trường có bao nhiêu học sinh trúng tuyển.
(2,0 điểm)
1. Chohình vẽ bên. Tính số đo góc \(\alpha \) và các độ dài \(x,y\) (góc làm tròn đến độ, độ dài làm tròn đến hàng phần trăm).
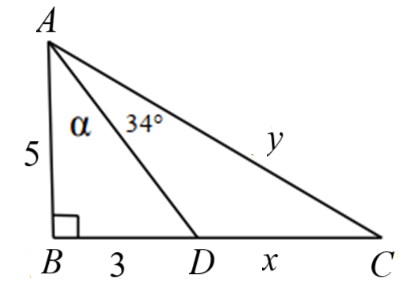
2.
Một người đứng cách nơi thả khinh khí cầu 800 m nhìn thấy nó với góc nghiêng \(38^\circ .\) Tính độ cao của khinh khí cầu so với mặt đất. Cho biết khoảng cách từ mặt đất đến mắt người đó là \(1,5\,\,{\rm{m}}\) (kết quả làm tròn đến hàng phần mười).
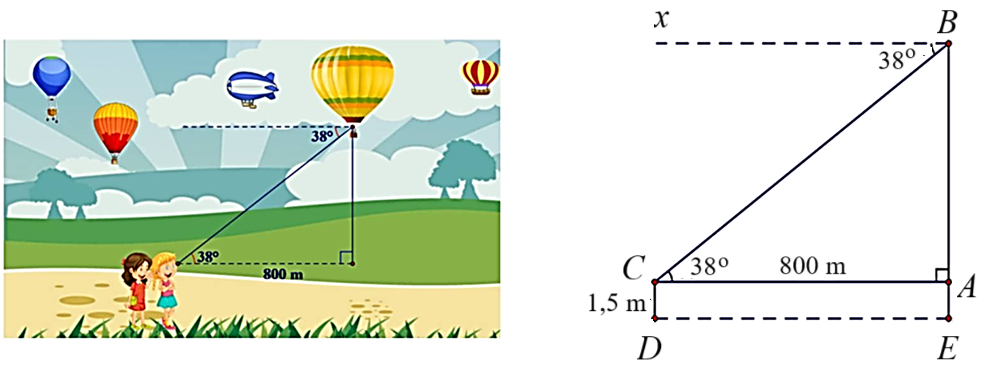
(0,5 điểm) Cho các số \[a,\,\,b,\,\,c\] không âm thỏa mãn \[a + b + c = 1\].
Chứng minh rằng \[T = {a^{2024}} + {b^{2023}} + {c^{2022}} - ab - bc - ca \le 1\].








