Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 6
17 câu hỏi
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
\[5x - 3z = 6\].
\(5x - 8y = 0.\)
\[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Phương trình \[x - 5y = 2\] nhận cặp số nào sau đây làm nghiệm?
\[\left( {1\,;\,\, - 2} \right)\].
\[\left( {3\,;\,\, - 1} \right)\].
\[\left( { - 1\,;\,\, - 3} \right)\].
\(\left( {7\,;\,\,1} \right).\)
Trên mặt phẳng tọa độ \[Oxy,\] cho các điểm \[A\left( {0\,;\,\,4} \right),{\rm{ }}B\left( {1\,;\,\,5} \right),{\rm{ }}C\left( {2\,;\,\,3} \right),{\rm{ }}D\left( {--1\,;\,\,--1} \right).\] Đường thẳng \[4x--3y = --1\] đi qua hai điểm nào trong các điểm đã cho?
\[A\] và \[B\].
\[B\] và \[C\].
\[C\] và \[D\].
\[D\] và \[A\].
Cặp số nào sau đây là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}x + y = 5\\2x - y = 4\end{array} \right.\]?
\[\left( { - 3\,;\,\,2} \right)\].
\[\left( {3\,;\,\,2} \right)\].
\[\left( {3\,;\,\, - 2} \right)\].
\[\left( { - 3\,;\,\, - 2} \right).\]
Điều kiện xác định của phương trình \(\frac{x}{{x - 3}} = \frac{{5x}}{{\left( {x + 2} \right)\left( {x - 3} \right)}}\) là
\[x \ne - 2;{\rm{ }}x \ne 3\].
\[x \ne 2;{\rm{ }}x \ne --3\].
\[x \ne - 3;{\rm{ }}x \ne --2\].
\[x \ne 0;{\rm{ }}x \ne 3\].
Bất đẳng thức \(m \le - 8\) có thể được phát biểu là
\(m\) lớn hơn âm 8.
\(m\) không nhỏ hơn âm 8.
\(m\) nhỏ hơn âm 8.
\(m\) không lớn hơn âm 8.
Nếu \[a < b\] thì 2a+1 ..... 2b+1. Dấu thích hợp điền vào ô trống là
\[ \ge \].
\[ \le \].
\[ < \].
</>
\[ > \].
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
\[3x + y > 4\].
\[0x - 4 \ge 0\].
\[5x--3 > 4\;\].
\[2{x^2} - 3x + 1 \le 0.\]
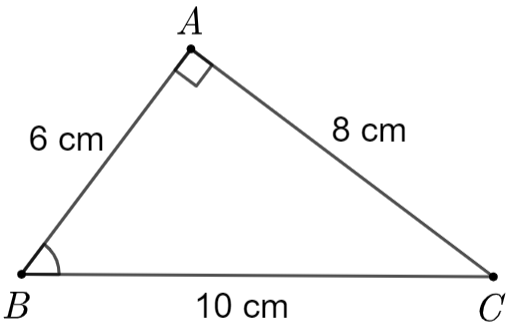
Cho \(\Delta ABC\) vuông tại \[A,\] có \[AB = 6{\rm{ cm}},{\rm{ }}AC = 8{\rm{ cm}},{\rm{ }}BC = 10{\rm{ cm}}.\] Khi đó \(\sin B\) bằng
\(\frac{3}{5}\).
\(\frac{4}{5}\).
\(\frac{5}{4}\).
\(\frac{5}{3}\).
Tam giác \[ABC\] vuông tại \[A\] thì
\[\sin B--\cos C = 0.\]
\[\sin C + \cos {\rm{ }}B = 0.\]
\[\sin {\rm{ }}B + \cos {\rm{ }}C = 0.\]
\[\cos B + \cos C = 0.\]
Cho tam giác \(ABC\) vuông tại \(A\) có \[BC = a,\] \[AC = b,\,\,AB = c.\] Khẳng định nào sau đây là đúng?
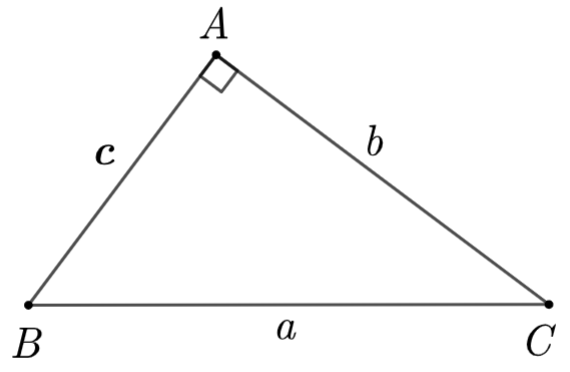
\[c = b \cdot \tan B\].
\[c = b \cdot \cot C\].
\[c = b \cdot \tan C\].
\[c = b \cdot \sin B\].
Cho tam giác\(ABC\)vuông tại\(A\)có \(AB = 8\,\,{\rm{cm}},\,\,\widehat C = 30^\circ .\) Độ dài cạnh \(BC\) là
4 cm.
\(8\sqrt 3 \,\,{\rm{cm}}\).
\(\frac{{8\sqrt 3 }}{3}\,\,{\rm{cm}}\).
16 cm.
(1,0 điểm) Giải các hệ phương trình sau:
a) \[\left\{ \begin{array}{l}x + y = 3\\3x - y = 5\end{array} \right.\];
b) \[\left\{ \begin{array}{l}2x + y = 4\\5x - y = 10\end{array} \right.\].
(2,0 điểm) Giải phương trình và bất phương trình sau:
a) \[2x\left( {3x - 1} \right) + 6x - 2 = 0\];
b) \(\frac{3}{{x + 1}} - \frac{2}{{x - 2}} = \frac{{4x - 2}}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\);
c) \[4x + 1 < 2x - 9\];
d) \(\frac{2}{3}\left( {2x + 3} \right) < 7 - 4x\).
(1,5 điểm) Một khu vườn hình chữ nhật có chu vi bằng \[68{\rm{ m}}.\] Nếu tăng chiều rộng lên gấp đôi và chiều dài lên gấp ba thì chu vi khu vườn mới là \[178{\rm{ m}}.\] Tính diện tích ban đầu của khu vườn.
(2,0 điểm)
1. Cho tam giác \[ABC\] vuông tại \[A\,\,\left( {AB < AC} \right)\], đường cao \(AH.\) Biết \(AB = 6\,\,{\rm{cm}}\) và \(\cos \widehat {ABC} = \frac{3}{5}\). Tính \(BC,\,\,AC,\,\,BH.\)
2. Từ trên một ngọn hải đăng cao \(75\,\,{\rm{m}}\), người ta quan sát hai lần thấy một chiếc thuyền đang hướng về phía hải đăng với góc hạ lần lượt là \(30^\circ \) và \(45^\circ \) (xem hình vẽ). Hỏi chiếc thuyền đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn kết quả đến hàng đơn vị)
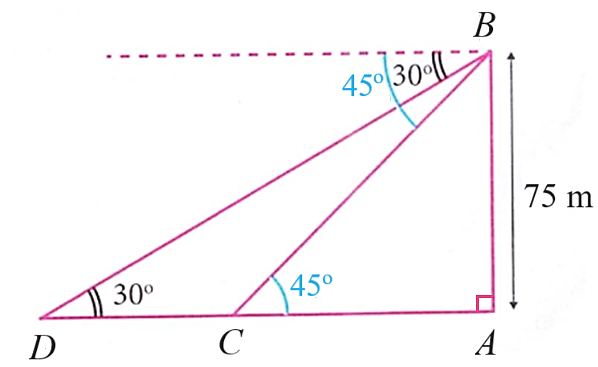

</>
(0,5 điểm) Cho \[x,{\rm{ }}y\] là hai số thực thỏa mãn điều kiện \[{x^2} + 2{y^2} + 2xy + 7x + 7y + 10 = 0.\]
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = \frac{{2x + 2y - 3}}{{x + y + 6}}.\)








