Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 10
13 câu hỏi
Cho phương trình \[4x - 7y = - 1{\rm{ }}\left( * \right)\]

Điều kiện xác định của phương trình \[\frac{1}{{x - 2}} + \frac{x}{{x + 1}} = - \frac{1}{2}\] là
\(x \ne 2.\)
\(x \ne - 1.\)
\[x \ne 2\] và \(x \ne - 1.\)
\(x \ne 2\) và \(x \ne 0.\)
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
\[2x + y \le 8\].
\[0x - 2 < 0\].
\[{x^2} - 5x + 4 > 0.\]
\[\frac{2}{3}x--1 \ge 5.\]
Cho tam giác \(DEF\) vuông tại \(D\) có đường cao \(DH\) và \(\widehat E = \alpha \). Khi đó \(\cot \alpha \) bằng tỉ số nào sau đây?
\(\frac{{EH}}{{DH}}\).
\(\frac{{DH}}{{EF}}\).
\(\frac{{DF}}{{EF}}\).
\(\frac{{DH}}{{EH}}\).
Trong tam giác \[ABC\], nếu \(\widehat B = 30^\circ \) thì tỉ số giữa cạnh đối \(AC\) và cạnh huyền \(BC\) bằng
\(\frac{{\sqrt 3 }}{2}.\)
\(\frac{1}{2}\).
\(\frac{{\sqrt 2 }}{2}.\)
1.
Cho hệ phương trình \[\left\{ \begin{array}{l}3x + y = 4\\2x - y = 11\end{array} \right.\] có nghiệm \[\left( {x\,;\,\,y} \right).\] Tính giá trị \[{x^2} - {y^2}\].
Cho phương trình \[\left( {x - 2} \right)\left( {3x + 5} \right) = \left( {2x - 4} \right)\left( {x + 1} \right)\]. Hỏi có bao nhiêu giá trị của \(x\) thỏa mãn phương trình đã cho?
Biển báo giao thông R.306 (hình bên báo tốc độ tối thiểu cho các xe cơ giới. Biển có hiệu lực bắt buộc các loại xe cơ giới vận hành với tốc độ không nhỏ hơn trị số ghi trên biển trong điều kiện giao thông thuận lợi và an toàn. Nếu một ô tô đi trên đường đó với tốc độ \(a\,\,\left( {{\rm{km/h}}} \right)\) thì \(a\) phải thỏa mãn điều kiện gì?

Cho tam giác \[ABC\] vuông tại \[C\] có \[BC = 1,2\,\,{\rm{cm}}\,{\rm{, }}AC = 0,9\,\,{\rm{cm}}.\] Tính \[\sin B + \cos B.\]
(2,0 điểm)
1) Giải các phương trình và bất phương trình sau:
a) \(\frac{{x + 3}}{{x + 1}} - \frac{{x - 1}}{x} = \frac{{{x^2} + 5x + 1}}{{x\left( {x + 1} \right)}};\)b) \(1 + \frac{{x + 4}}{5} \le x - \frac{{x + 3}}{3}\).
2) Xác định \[a,\,\,b\] để đồ thị hàm số \[y = ax + b\] đi qua hai điểm \[A\left( {2\,;\,\,1} \right)\] và \[B\left( {4\,;\,\,--2} \right).\]
(1,5 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Do ảnh hưởng của dịch Covid – 19 nên trong tháng hai cả hai tổ công nhân chỉ làm được 700 sản phẩm. Sang tháng ba, tình hình dịch ổn định tổ I vượt mức \[20\% ,\] tổ II vượt mức \[15\% \] nên cả hai tổ làm được 830 sản phẩm. Hỏi trong tháng hai mỗi tổ làm được bao nhiêu sản phẩm?
(2,0 điểm)
1) Cho tam giác \(ABC\) có \(BC = 16\,{\rm{cm}},\,\,\widehat {ABC} = 45^\circ ,\,\,\widehat {ACB} = 30^\circ .\) Gọi \(N\) là chân đường vuông góc kẻ từ \(A\) đến cạnh \(BC.\) Tính độ dài cạnh \(AN\) (làm tròn kết quả đến chữ số thập phân thứ hai).
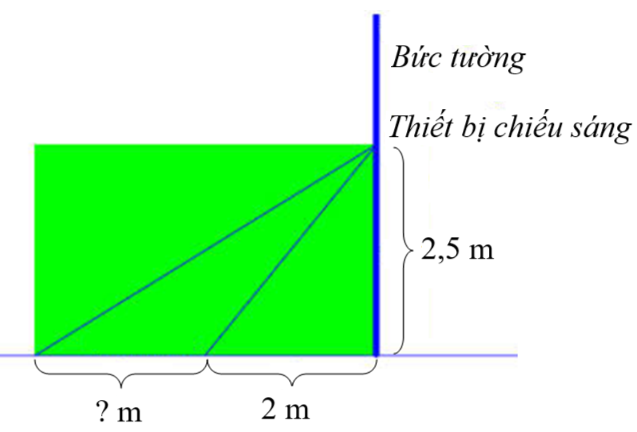
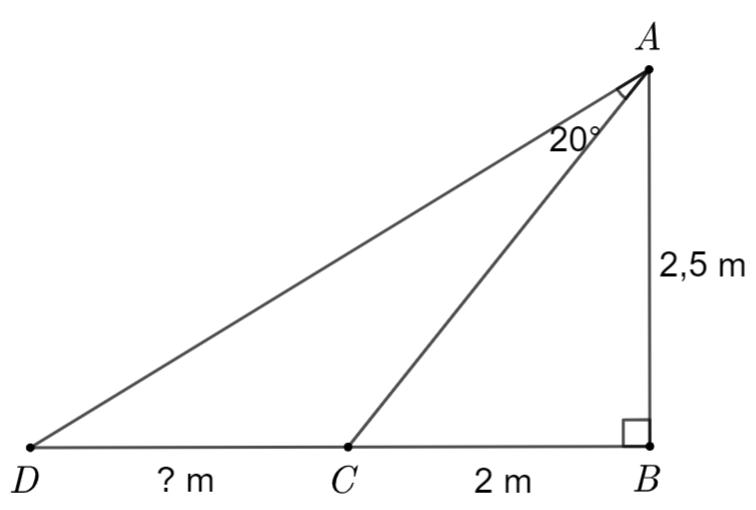
2) Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm như hình vẽ. Thiết bị này có góc chiếu sáng là \(20^\circ \) và cần đặt cao hơn mặt đất là \(2,5\,\,{\rm{m}}.\) Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường \(2\,\,{\rm{m}}\) (như hình vẽ). Tính độ dài vùng được chiếu sáng trên mặt đất (làm tròn kết quả đến chữ số thập phân thứ nhất)
(0,5 điểm) Cho hai số thực \[a,\,\,b\] thỏa mãn \[a + b \ne 0.\] Chứng minh \({a^2} + {b^2} + {\left( {\frac{{ab + 1}}{{a + b}}} \right)^2} \ge 2.\)








