Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án - Đề 6
15 câu hỏi
Mẫu thức chung của phương trình \[\frac{1}{{x - 1}} + \frac{3}{{x + 1}} = 0\] là
\(\left( {x - 1} \right)\left( {x + 1} \right)\).
\({\left( {x - 1} \right)^2}\).
\({\left( {x + 1} \right)^2}\).
\(x\left( {x - 1} \right)\left( {x + 1} \right)\).
Gọi \(S\) là tập hợp tất cả các nghiệm của phương trình \[ - 4\left( {x - 5} \right)\left( {9 - 3x} \right) = 0\]. Khẳng định nào sau đây là đúng?
\[S = \left\{ { - 5;\,\,3} \right\}.\]
\[S = \left\{ {5;\,\, - 3} \right\}.\]
\[S = \left\{ { - 5;\,\, - 3} \right\}.\]
\[S = \left\{ {5;\,\,3} \right\}.\]
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
\[5x - 3z = 6\].
\(5x - 8y = 0.\)
\[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Cặp số \(\left( { - 2;\,\, - 3} \right)\) là nghiệm của hệ phương trình nào sau đây?
\(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 3}\\{2x + y = 4}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{2x - y = - 1}\\{x - 3y = 8}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{2x - y = - 1}\\{x - 3y = 7}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{4x - 2y = 0}\\{x + y = - 5}\end{array}} \right.\).
Bất đẳng thức \(m \le - 8\) có thể được phát biểu là
\(m\) lớn hơn âm 8.
\(m\) không nhỏ hơn âm 8.
\(m\) nhỏ hơn âm 8.
\(m\) không lớn hơn âm 8.
Trong các khẳng định sau, khẳng định nào là đúng?
\(a < b\) và \(c > d\) thì \(a + b < c + d\).
>>
\(a < b\) và \(c > d\) thì \(a + c = b + d\).>
\(a > b\) và \(c > d\) thì \(ac > bd\).
\(a > b\) và \(c > d\) thì \(a + c > b + d\).
Khi biến đổi bất phương trình \[ - 15x + 4 \le 0\] về bất phương trình có dạng \(A\left( x \right) \ge B\), trong đó \(A\left( x \right)\) không chứa hệ số tự do, thì đa thức \(A\left( x \right)\) là
\[ - 15x + 4\].
\[ - 15x\].
\[15x - 4\].
\[15x\].
Với giá trị nào sau đây của \(m\) thì phương trình \(x - 1 = 3m + 5\) có nghiệm dương?
\(m \ge - 2\).
\(m > - 2\).
\(m \le - 2\).
\(m < - 2\).
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\cos \widehat {MNP}\) bằng
\(\frac{{MN}}{{NP}}\).
\(\frac{{MP}}{{NP}}\).
\(\frac{{MN}}{{MP}}\).
\(\frac{{MP}}{{MN}}\).
Cho \(\alpha = 40^\circ \) và \(\beta = 50^\circ .\) Khẳng định nào sau đây là đúng?
\(\sin \alpha = \sin \beta \).
\(\cos \alpha = \cos \beta \).
\(\tan \alpha = \cot \beta \).
\(\tan \alpha = \tan \beta \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10,\,\,\widehat C = 30^\circ .\) Số đo góc \[\widehat {B\,}\] và độ dài cạnh \(BC\) (làm tròn kết quả đến hàng phần trăm) bằng
\(\widehat B = 60^\circ ;\) \(BC = 20.\)
\(\widehat B = 60^\circ ;\) \(BC \approx 8,08.\)
\(\widehat B = 60^\circ ;\) \(BC \approx 11,55\).
\(\widehat B = 60^\circ ;\) \(BC \approx 14,14.\)
(2,0 điểm)
1. Giải các phương trình sau:
a) \(\left( {6x - 7} \right)\left( {3x + 4} \right) = \left( {7 - 6x} \right)\left( {x - 1} \right)\).
b) \(\frac{3}{{x + 1}} - \frac{2}{{x - 2}} = \frac{{4x - 2}}{{\left( {x + 1} \right)\left( {2 - x} \right)}}\).
2. Giải các bất phương trình sau:
a) \(\frac{{6 - 4x}}{{ - 5}} < 1\).
b) \[{\left( {x + 2} \right)^2} - \left( {x + 5} \right)\left( {x - 5} \right) > 2\left( {2x - 5} \right)\].
(2,5 điểm)
1. Tìm các hệ số \(x\) và \(y\) trong phản ứng hóa học đã được cân bằng sau:
\[x{\rm{Fe}}{\left( {{\rm{OH}}} \right)_3} \to {\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3} + y{{\rm{H}}_2}{\rm{O}}.\]
Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một đoàn khách du lịch gồm 40 người dự định tham quan chùa Hương (Hà Nội) bằng cáp treo khứ hồi (gồm lượt lên và lượt xuống). Nhưng khi tới nơi có 5 bạn trẻ muốn khám phá bằng đường bộ khi leo lên còn lúc xuống sẽ đi cáp treo để trải nghiệm nên 5 bạn chỉ mua vé lượt xuống, do đó đoàn đã chi ra \[8{\rm{ }}450{\rm{ }}000\] đồng để mua vé. Hỏi giá vé cáp treo khứ hồi và giá vé cáp treo 1 lượt là bao nhiêu? Biết rằng giá vé 1 lượt rẻ hơn giá vé khứ hồi là \[70{\rm{ }}000\] đồng.
(Giá vé tính tại thời điểm tháng 2 năm 2024)
(2,0 điểm)
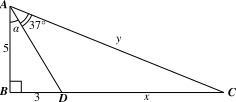
1. Cho hình vẽ bên. Tính số đo góc \(\alpha \) và các độ dài \(x,y\) (góc làm tròn đến độ và độ dài làm tròn đến hàng phần trăm).
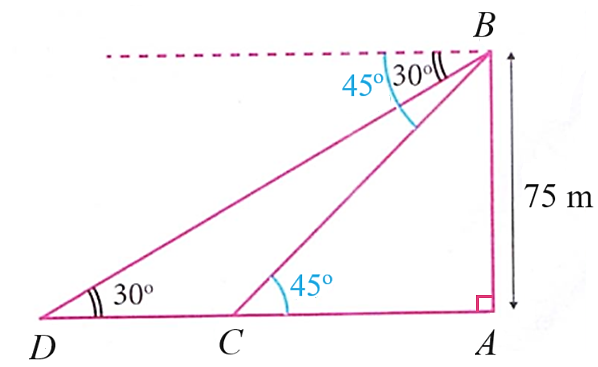
2. Từ trên một ngọn hải đăng cao \(75\,\,{\rm{m}}\), người ta quan sát hai lần thấy một chiếc thuyền đang hướng về phía hải đăng với góc hạ lần lượt là \(30^\circ \) và \(45^\circ \) (xem hình vẽ). Hỏi chiếc thuyền đi được bao nhiêu mét giữa hai lần quan sát (làm tròn kết quả đến hàng đơn vị)?

(0,5 điểm) Cho \(a,\,\,b,\,\,c\) là ba số không âm.
Chứng minh bất đẳng thức \({a^3} + {b^3} \ge {a^2}b + {b^2}a = ab\left( {a + b} \right).\,\,\,\left( 1 \right)\)
Áp dụng bất đẳng thức (1), chứng minh bất đẳng thức sau:
\(\frac{1}{{{a^3} + {b^3} + abc}} + \frac{1}{{{b^3} + {c^3} + abc}} + \frac{1}{{{c^3} + {a^3} + abc}} \le \frac{1}{{abc}}\).








