Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án - Đề 4
11 câu hỏi
Điều kiện xác định của phương trình \(\frac{x}{{x - 3}} = \frac{{5x}}{{\left( {x + 2} \right)\left( {x - 3} \right)}}\) là
\[x \ne - 2;{\rm{ }}x \ne 3\].
\[x \ne 2;{\rm{ }}x \ne --3\].
\[x \ne - 3;{\rm{ }}x \ne --2\].
\[x \ne 0;{\rm{ }}x \ne 3\].
Phương trình \(0x + 7y = 14\) có nghiệm tổng quát là
\(\left( {x;\,\,2} \right)\) với \(x \in \mathbb{R}\).
\(\left( {2;\,\,y} \right)\) với \(y \in \mathbb{R}\).
\(\left( {x;\,\,0} \right)\) với \(x \in \mathbb{R}\).
\(\left( {0;\,\,y} \right)\) với \(y \in \mathbb{R}\).
Cho \(\alpha \) và \(\beta \) là hai góc nhọn bất kì thỏa mãn \[\alpha + \beta = 90^\circ \] và \[\sin \alpha = 0,5.\] Khẳng định nào sau đây là đúng?
\[\sin \beta = 0,5.\]
\[\cos \beta = 0,5.\]
\[\tan \beta = 0,5.\]
\[\cot \beta = 0,5.\]
Xét tam giác \[ABC\] vuông tại \(A\) có đường cao \(AH\). Khi đó \(\sin \widehat {HAC}\) bằng
\(\frac{{AH}}{{AC}}\).
\(\frac{{AH}}{{HC}}\).
\(\frac{{AB}}{{BC}}\).
\(\frac{{AC}}{{BC}}\).
Cho ba số \(a,\,\,b,\,\,c\) và \(a \le b.\)
a) \(a + c \le b + c.\)
b) \(ac \ge bc\) với \(c > 0.\)
c) \( - \frac{a}{c} \ge - \frac{b}{c}\) với \(c < 0.\)
d) \({a^2} \le {b^2}.\)
Gọi \(\left( {x;\,\,y} \right)\) là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}2\left( {x + y} \right) + 3\left( {x - y} \right) = 4\\\left( {x + y} \right) + 2\left( {x - y} \right) = 5\end{array} \right..\] Bạn An sau khi giải hệ phương trình thì viết được hệ thức \(y = ax.\) Tìm \(a.\)
Cho tam giác \(ABC\) có \(AB = 5{\rm{\;cm}},\,\,BC = 12{\rm{\;cm}}\) và \(CA = 13{\rm{\;cm}}.\) Tính số đo góc \(C\) (làm tròn kết quả đến phút).
(2,5 điểm)
1. Giải các phương trình sau:
a) \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0.\)
b) \(\frac{{x + 3}}{{x - 3}} = \frac{3}{{{x^2} - 3x}} + \frac{1}{x}.\)
2. Giải các bất phương trình sau:
a) \(\frac{{3 - 2x}}{2} > 4\).
b) \(\left( {x - 3} \right)\left( {x + 3} \right) < {\left( {x + 2} \right)^2} + 3\).
c) \[\frac{{4x - 1}}{2} + \frac{{6x - 19}}{6} \ge \frac{{9x - 11}}{3}.\]
(2,0 điểm)
1. Tìm các hệ số \(x\) và \(y\) trong phản ứng hóa học đã được cân bằng sau:
\(x{\rm{FeO}} + y{{\rm{O}}_2}\mathop \to \limits^{{\rm{t}}^\circ } 2{\rm{F}}{{\rm{e}}_3}{{\rm{O}}_4}.\)
Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Gen B có \(3\,\,600\) liên kết hydrogen và có hiệu giữa nucleotide loại \[T\] với loại nucleotide không bổ sung với nó là \(300\) nucleotide. Tính số nucleotide từng loại của gen B. Biết rằng, để tính số lượng nucleotide \[\left( {A,{\rm{ }}T,{\rm{ }}G,{\rm{ }}C} \right)\] trong phân tử DNA, ta áp dụng nguyên tắc bổ sung: “\[A\] liên kết với \[T\] bằng 2 liên kết hydrogen và \[G\] liên kết với \[C\] bằng 3 liên kết hydrogen” và \(\% A = \% T,\,\,\% G = \% C.\) Tổng số nucleotide trong gen:
\(N = A + T + G + C = 2A + 2G = 2T + 2C.\)
(2,5 điểm)
1. Cho tam giác \(OPQ\) vuông tại \(O\) có \(\widehat {Q\,} = 35^\circ \) và \(OQ = 10{\rm{ cm}}{\rm{.}}\) Tính độ dài các cạnh còn lại của tam giác \(OPQ\) (làm tròn kết quả đến hàng phần trăm đối với đơn vị của cm).
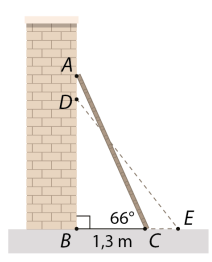
2. Một chiếc thang \(AC\) được dựng vào một bức tường thẳng đứng (hình vẽ).
– Ban đầu khoảng cách từ chân thang đến tường là \(BC = 1,3{\rm{\;m}}\) và góc tạo bởi thang và phương nằm ngang là \(\widehat {ACB} = 66^\circ \).
– Sau đó, đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}}\) đến vị trí \(D.\) Khi đó, góc \(DEB\) tạo bởi thang và phương nằm ngang bằng bao nhiêu (Kết quả số đo góc làm tròn đến phút)?
(0,5 điểm) Cho góc \(\alpha \) thỏa mãn \[0^\circ < \alpha < 90^\circ .\] Chứng minh rằng: \[\frac{{\sin \alpha + \cos \alpha - 1}}{{1 - \cos \alpha }} = \frac{{2\cos \alpha }}{{\sin \alpha - \cos \alpha + 1}}.\]








