12 câu hỏi
Đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) (với \(a,\,\,b\) là hằng số) có hệ số là
\[ - 36{a^2}{b^2}\].
\[ - 36\].
\[36{a^2}{b^2}\].
\[ - 36{a^2}\].
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3{x^2}y\)?
\(3{x^2}yz\).
\(\frac{1}{2}xyx\).
\(x{y^2}\).
\( - 3{x^2}z\).
Tích của đa thức \[6xy\]và đa thức \[2{x^2} - 3y\]là đa thức
\[12{x^2}y + 18x{y^2}\].
\[12{x^3}y - 18x{y^2}\].
\[12{x^3}y + 18x{y^2}\].
\[12{x^2}y - 18x{y^2}\].
Điều kiện của số tự nhiên \(n\)để phép chia \(\left( {4{x^{10}}y - x{y^7} + {x^5}{y^4}} \right):2{x^n}{y^n}\)là phép chia hết là
\(n = 0\).
\(n = 1\).
\(n = 5\).
\(n \in \left\{ {0\,;\,\,1} \right\}\).
Hằng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) có tên là
bình phương của một tổng.
bình phương của một hiệu.
tổng hai bình phương.
hiệu hai bình phương.
Kết quả của khai triển phép tính \({\left( {\frac{1}{2}x - 1} \right)^2}\) là
\(\frac{1}{2}{x^2} - \frac{1}{2}x + 1\).
\(\frac{1}{4}{x^2} - 1\).
\(\frac{1}{4}{x^2} - \frac{1}{2}x + 1\).
\(\frac{1}{4}{x^2} - x + 1\).
Phân thức\(\frac{A}{B}\) xác định khi nào?
\(B < 0\).
\(B = 0\).
\(B \ne 0\).
\(B > 0\).
Phân thức nào sau đây bằng với phân thức \(\frac{y}{{3x}}\) (với giả thiết các phân thức đều có nghĩa)?
\(\frac{{3{y^2}}}{{9x{y^2}}}\).
\(\frac{{{y^2}}}{{9x{y^2}}}\).
\(\frac{{3{y^2}}}{{9xy}}\).
\(\frac{{3y}}{{9x{y^2}}}\).
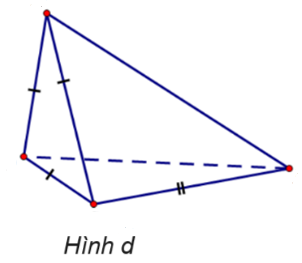
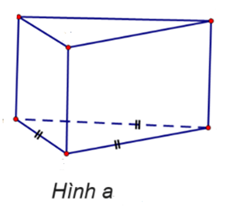
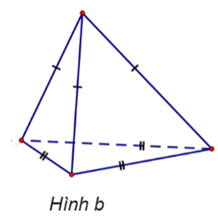
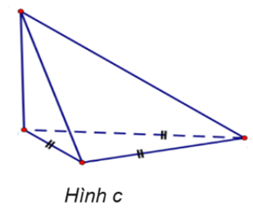
Cho các hình vẽ sau:
|
|
|
|
Trong những hình dưới đây, những hình nào là hình chóp tam giác đều?
Hình a.
Hình b.
Hình c.
Hình d.
Thể tích của hình chóp tam giác đều bằng
diện tích đáy nhân với chiều cao.
\(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(\frac{1}{2}\) chiều cao nhân với diện tích đáy.
\(\frac{3}{2}\) diện tích đáy nhân với chiều cao.
Độ dài cạnh \(BC\) trong \(\Delta ABC\) cân tại \(A\) ở hình vẽ bên là
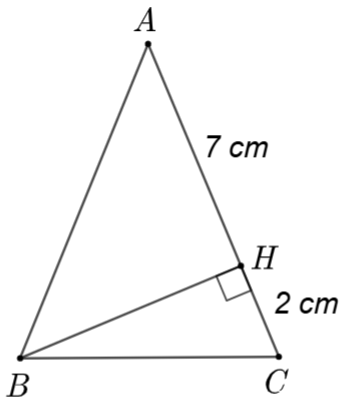
\(4\;\;{\rm{cm}}\).
\(5\;\;{\rm{cm}}\).
\(6\;\;{\rm{cm}}\).
\(7\;\;{\rm{cm}}\).
Trong các khẳng định sau, khẳng định nào đúng?
Tứ giác có 4 cạnh, 2 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 3 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 4 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 1 đường chéo, 4 đỉnh và 4 góc.