Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh Diều có đáp án - Đề 8
76 câu hỏi
Góc có số đo \[\frac{{3\pi }}{5}\] đổi sang độ là
\[240^\circ \].
\[135^\circ \].
\[108^\circ \].
\[270^\circ \].
Cho góc \(\alpha \) thỏa \( - \frac{{3\pi }}{2} < \alpha < - \pi \). Mệnh đề nào sau đây là đúng?
\(\cos \alpha > 0\).
\(\cot \alpha > 0\).
\(\sin \alpha > 0\).
\(\tan \alpha > 0\).
Với góc \[\alpha \] bất kỳ, đẳng thức nào sau đây là đúng?
\[\cos \left( {\pi - \alpha } \right) = \cos \alpha \].
\[\cos \left( {\pi - \alpha } \right) = - \cos \alpha \].
\[\sin \left( {\pi - \alpha } \right) = - \sin \alpha \].
\[\tan \left( {\pi - \alpha } \right) = \tan \alpha \].
Khẳng định nào sau đây là sai?
\(\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}.\)
\(\cos a--\cos b = 2\sin \frac{{a + b}}{2}.\sin \frac{{a - b}}{2}.\)
\(\sin a + \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}.\)
\(\sin a--\sin b = 2\cos \frac{{a + b}}{2}.\sin \frac{{a - b}}{2}.\)
Cho \(\sin a = \frac{3}{5},0 < a < \frac{\pi }{2}.\) Giá trị biểu thức \(M = \sin \left( {a - \frac{\pi }{4}} \right)\) bằng
\(M = - \frac{{\sqrt 2 }}{{10}}\).
\(M = - \frac{{\sqrt 2 }}{{10}}\).
\(M = - \frac{{\sqrt 2 }}{{10}}\).
\(M = - \frac{{\sqrt 2 }}{{10}}\).
Nếu \(\sin \alpha + \cos \alpha = \frac{3}{2}\) thì \(\sin 2\alpha \) bằng
\(\frac{5}{4}\).
\(\frac{1}{2}\).
\(\frac{{13}}{4}\).
\(\frac{9}{4}\).
Rút gọn biểu thức \(A = \frac{{\sin 3x + \cos 2x - \sin x}}{{\cos x + \sin 2x - \cos 3x}}\,\,\,\left( {\sin 2x \ne 0;2\sin x + 1 \ne 0} \right)\) ta được
\(A = \cot 6x\).
\(A = \cot 3x\).
\(A = \cot 2x\).
\(A = \tan x + \tan 2x + \tan 3x\).
Gọi \(M = \cos \left( {a + b} \right).\cos \left( {a - b} \right) + \sin \left( {a + b} \right).\sin \left( {a - b} \right)\). Ta có:
\(M = 1 - 2{\sin ^2}b\).
\(M = 1 + 2{\sin ^2}b\).
\(M = \cos 4b\).
\(M = \sin 4b\).
Hàm số \(y = \sin 2x\) có chu kỳ là
\(T = 2\pi \).
\(T = \frac{\pi }{2}\).
\(T = \pi \).
\(T = 4\pi \).
Tập xác định của hàm số \[y = \cot x\] là
\({\rm{D}} = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}.\)
\({\rm{D}} = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\)
\({\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
\({\rm{D}} = \mathbb{R}.\)
Hàm số nào sau đây có tính đơn điệu trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) khác với các hàm số còn lại?
\(y = \sin x\).
\(y = \cos x\).
\(y = \tan x\).
\(y = - \cot x\).
Xét sự biến thiên của hàm số \(y = 1 - \sin x\) trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai?
Hàm số đã cho nghịch biến trên khoảng \(\left( { - \frac{\pi }{2};\,0} \right).\)
Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\,\frac{\pi }{2}} \right).\)
Hàm số đã cho đồng biến trên khoảng\(\,\,\left( {\frac{\pi }{2};\,\pi } \right).\)
Hàm số đã cho nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\,\frac{{3\pi }}{2}} \right).\)
Giá trị lớn nhất của hàm số \(y = 1 - 2\cos x - {\cos ^2}x\) là
\[2\].
\[5\].
\[0\].
\[3\].
Trong các hàm số dưới đây có bao nhiêu hàm số là hàm số chẵn?
\[y = {\rm{cos}}3x\,\,\left( 1 \right)\]; \[y = {\rm{sin }}\left( {{x^2} + 1} \right){\rm{ }}\left( 2 \right)\]; \[y = {\rm{ta}}{{\rm{n}}^2}x\;\,\,\,\left( 3 \right)\]; \[y = {\rm{cot }}x\,\,\;\left( 4 \right)\].
\[1\].
\[2\].
\[3\].
\[4\].
Phương trình \[\sin x = \sin \alpha \] có nghiệm là
\[\left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.;k \in \mathbb{Z}\]
\[\left[ \begin{array}{l}x = \alpha + k\pi \\x = \pi - \alpha + k\pi \end{array} \right.;k \in \mathbb{Z}\].
\[\left[ \begin{array}{l}x = \alpha + k\pi \\x = - \alpha + k\pi \end{array} \right.;k \in \mathbb{Z}\].
\[\left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.;k \in \mathbb{Z}\].
Mệnh đề nào sau đây là đúng?
\(\cos x \ne 1 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(\cos x \ne - 1 \Leftrightarrow x \ne - \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Nghiệm phương trình: \(1 + \tan x = 0\) là
\(x = \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Gọi \(X\) là tập nghiệm của phương trình \(\cos \left( {\frac{x}{2} + 15^\circ } \right) = \sin x\). Khi đó
\(290^\circ \in X\).
\(250^\circ \in X\).
\(220^\circ \in X\).
\(240^\circ \in X\).
Phương trình \[\tan \frac{x}{2} = \tan x\] có nghiệm là
\[x = k2\pi ,k \in \mathbb{Z}\].
\[x = k\pi ,k \in \mathbb{Z}\].
\[x = \pi + k2\pi ,k \in \mathbb{Z}\].
Cả A, B, C đều sai.
Số nghiệm \(x \in \left[ {0;14} \right]\) của phương trình \[\cos 3x - 4\cos 2x + 3\cos x - 4 = 0\] là
\[1\].
\[2\].
\[3\].
\[4\].
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{a{n^2}}}{{n + 1}}\)\[(a\] là hằng số). Số hạng \({u_{n + 1}}\) là số hạng nào sau đây?
\({u_{n + 1}} = \frac{{a.{{\left( {n + 1} \right)}^2}}}{{n + 2}}\).
\({u_{n + 1}} = \frac{{a.{{\left( {n + 1} \right)}^2}}}{{n + 1}}\).
\({u_{n + 1}} = \frac{{a.{n^2} + 1}}{{n + 1}}\).
\({u_{n + 1}} = \frac{{a{n^2}}}{{n + 2}}\).
Cho dãy số có các số hạng đầu là:\(8,15,22,29,36,...\). Số hạng tổng quát của dãy số này là
\({u_n} = 7n + 7\).
\({u_n} = 7.n\).
\({u_n} = 7.n + 1\).
Không viết được dưới dạng công thức.
Cho dãy số \(({u_n})\) được xác định bởi \({u_n} = \frac{{{n^2} + 3n + 7}}{{n + 1}}\). Năm số hạng đầu của dãy là
\(\frac{{11}}{2};\frac{{17}}{3};\frac{{25}}{4};7;\frac{{47}}{6}\).
\(\frac{{13}}{2};\frac{{17}}{3};\frac{{25}}{4};7;\frac{{47}}{6}\).
\(\frac{{11}}{2};\frac{{14}}{3};\frac{{25}}{4};7;\frac{{47}}{6}\).
\(\frac{{11}}{2};\frac{{17}}{3};\frac{{25}}{4};8;\frac{{47}}{6}\).
Khẳng định nào sau đây là đúng với dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {( - 1)^n}\) ?
\(\left( {{u_n}} \right)\) bị chặn.
\(\left( {{u_n}} \right)\) không bị chặn.
\(\left( {{u_n}} \right)\) bị chặn trên.
\(\left( {{u_n}} \right)\) bị chặn dưới.
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_n} = \sqrt {n - 1} \) với \(n \in {\mathbb{N}^*}.\) Khẳng định nào sau đây là sai?
5 số hạng đầu của dãy là: \(0;1;\sqrt 2 ;\sqrt 3 ;\sqrt 5 \).
Số hạng \({u_{n + 1}} = \sqrt n \).
Là dãy số tăng.
Bị chặn dưới bởi số \(0\).
Trong mặt phẳng \(\left( \alpha \right)\) cho tứ giác \(ABCD\), điểm \(E \notin \left( \alpha \right)\). Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm \(A,B,C,D,E\)?
\[6\].
\[7\].
\[8\].
\[9\].
Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là
5 mặt, 5 cạnh.
6 mặt, 5 cạnh.
6 mặt, 10 cạnh.
5 mặt, 10 cạnh.
Cho tứ diện \(ABCD\). \(G\) là trọng tâm tam giác \(BCD\). Giao tuyến của hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\) là
\[AM\], \[M\] là trung điểm \[AB\].
\[AH,\]\[H\] là hình chiếu của \[B\] trên \[CD.\]
\[AN\], \[N\] là trung điểm \[CD\].
\[AK,\]\[K\] là hình chiếu của \[C\] trên \[BD.\]
Cho hình chóp tứ giác \[S.ABCD\], gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD\]. Một mặt phẳng \[\left( \alpha \right)\] cắt các cạnh bên \[SA,SB,SC,SD\] tương ứng tại các điểm \[M,N,P,Q\]. Khẳng định nào đúng?
Các đường thẳng \[MP,NQ,SO\] đồng quy.
Các đường thẳng \[MP,NQ,SO\] chéo nhau.
Các đường thẳng \[MP,NQ,SO\] song song.
Các đường thẳng \[MP,NQ,SO\] trùng nhau.
Cho đường thẳng \[a\] nằm trên \[mp\left( P \right),\] đường thẳng \[b\] cắt \[\left( P \right)\] tại \[O\] và \[O\] không thuộc \[a\]. Vị trí tương đối của \[a\] và \[b\] là
chéo nhau.
cắt nhau.
trùng nhau.
song song nhau.
Khẳng định nào sau đây là đúng?
Nếu ba mặt phẳng cắt nhau theo ba giao tuyến thì ba giao tuyến đó đồng quy.
Nếu hai mặt phẳng lần lượt chứa hai đường thẳng song song thì giao tuyến, nếu có, của chúng sẽ song song với cả hai đường thẳng đó.
Nếu hai đường thẳng \[a\] và \[b\] chéo nhau thì có hai đường thẳng \[p\] và \[q\] song song nhau mà mỗi đường đều cắt cả \[a\] và\[b\] .
Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
Cho hình chóp\[S.ABCD\]. Gọi \[M,\,\,N,\,\,P,\,\,Q,\,\,R,\,\,T\] lần lượt là trung điểm\[AC\], \[BD\], \[BC,\]\[CD\], \[SA\],\[SD\]. Bốn điểm nào sau đây đồng phẳng?
\[M,P,R,T.\]
\[M,Q,T,R.\]
\[M,N,R,T.\]
\[P,Q,R,T.\]
Cho hình chóp \[{\rm{S}}.ABCD\] đáy là hình bình hành tâm O, I là trung điểm của \[SC\], xét các mệnh đề:
(1) Đường thẳng \[IO\] song song với \[SA\].
(2) Mặt phẳng \[\left( {IBD} \right)\] cắt các cạnh của hình chóp \[S.ABCD\] theo một hình tứ giác.
(3) Giao điểm của đường thẳng \[AI\] với mặt phẳng \[\left( {SBD} \right)\] là trọng tâm của tam giác \[\left( {SBD} \right)\].
(4) Giao tuyến của hai mặt phẳng \[\left( {IBD} \right)\]và \[\left( {SAC} \right)\] là \[IO\].
Số mệnh đề đúng trong các mệnh để trên là
2.
4.
3.
1.
Cho ba đường thẳng đôi một chéo nhau \(a,\;b,\;c\). Gọi \(\left( P \right)\) là mặt phẳng qua \(a\), \(\left( Q \right)\) là mặt phẳng qua \(b\) sao cho giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) song song với \(c\). Có nhiều nhất bao nhiêu mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) thỏa mãn yêu cầu trên?
Vô số mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Một mặt phẳng \(\left( P \right)\), vô số mặt phẳng \(\left( Q \right)\).
Một mặt phẳng \(\left( Q \right)\), vô số mặt phẳng \(\left( P \right)\).
Một mặt phẳng \(\left( P \right)\), một mặt phẳng\(\left( Q \right)\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành tâm \[O\]. Lấy điểm \[I\] trên đoạn \[SO\] sao cho \[\frac{{SI}}{{SO}} = \frac{2}{3}\], \[BI\] cắt \[SD\] tại \[M\] và \[DI\] cắt \[SB\] tại \[N\]. Tứ giác \[MNBD\] là hình gì?
Hình thang.
Hình bình hành.
Hình chữ nhật.
Tứ diện vì \[MN\] và \[BD\] chéo nhau.
PHẦN II. TỰ LUẬN (3,0 điểm)
(1,5 điểm)
a) Tính giá trị lượng giác \[\tan \left( {\alpha + \frac{\pi }{3}} \right)\] khi \[\sin \alpha = \frac{3}{5},\,\,\frac{\pi }{2} < \alpha < \pi \].
b) Giải phương trình \(\cos \left( {\frac{\pi }{3} + 3x} \right) + \cos \left( {\frac{{2\pi }}{3} - 4x} \right) + \cos x = 1.\)
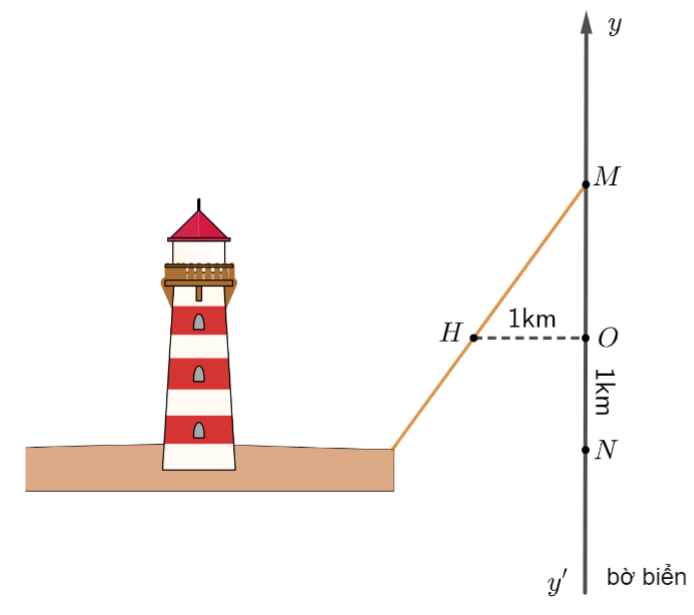
c) Ngọn đèn trên hải đăng \(H\) cách bờ biển \(yy'\)một khoảng \(HO = 1\,{\rm{km}}\). Đèn xoay ngược chiều kim đồng hồ với tốc độ \(\frac{\pi }{{10}}\,{\rm{rad}}/{\rm{s}}\) và chiếu hai luồng ánh sáng về hai phía đối diện nhau. Khi đèn xoay, điểm \(M\) mà luồng ánh sáng của hải đăng rọi vào bờ biển chuyển động dọc theo bờ. Ban đầu luồng sáng trùng với đường thẳng \(HO\). |
|
Viết hàm số biểu thị toạ độ \({y_M}\) của điểm \(M\) trên trục \(Oy\) theo thời gian \(t\) và xác định thời điểm \(t\) mà đèn hải đăng chiếu vào ngôi nhà \(N\) nằm trên bờ biển với toạ độ \({y_N} = - 1\,\left( {{\rm{km}}} \right)\).
(0,5 điểm) Chứng minh rằng dãy số \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = \sqrt 2 }\\{{u_{n + 1}} = \sqrt {{u_n} + 2} }\end{array}} \right.\) tăng và bị chăn trên bởi 2.
(1,0 điểm) Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(M\) và \(P\) là hai điểm di dộng trên các cạnh \(AD\) và \(BC\), sao cho \(MA = PC = x\)\(\left( {0 < x < a} \right)\). Mặt phẳng \(\left( \alpha \right)\) qua \(MP\) song song với \(CD\) cắt \(AC,\,\,BD\) lần lượt tại \(N,Q.\)
a) Chứng minh tứ giác \(MNPQ\) là hình thang cân.
b) Tính diện tích hình thang cân \(MNPQ\) theo \[a\] và \[x\]. Tìm \(x\) để diện tích đó nhỏ nhất.
PHẦN I. TRẮC NGHIỆM (7 điểm)
Mệnh đề kéo theo \(P \Rightarrow Q\) sai khi
\(P\) sai và \(Q\) đúng;
\(P\) sai và \(Q\) sai;
\(P\) đúng và \(Q\) sai;
\(P\) đúng và \(Q\) đúng.
Viết mệnh đề sau bằng cách sử dụng kí hiệu \(\forall \) hoặc \(\exists \): “Cho hai số thực khác nhau bất kì luôn tồn tại một số hữu tỉ nằm giữa hai số thực đã cho”.
\(\forall a,b \in \mathbb{R},a < b,\exists r \in \mathbb{Q}:a < r < b\);
\(\forall a,b \in \mathbb{R},\forall r \in \mathbb{Q}:a < r < b\);
\(\forall a,b \in \mathbb{R},a < b,\forall r \in \mathbb{Q}:a < r < b\)
\(\exists a,b \in \mathbb{R},\exists r \in \mathbb{Q}:a < r < b\).
Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề: “Mọi học sinh của lớp 10A đều thích học môn Toán”?
“Tất cả các bạn học sinh trong lớp 10A đều không thích môn Toán”;
“Có một học sinh của lớp 10A thích học môn Toán”;
“Có một học sinh trong lớp 10A không thích học môn Toán”;
“Mọi học sinh trong lớp 10A đều không thích học môn Toán”.
Cho tập hợp \(A = \left\{ {x \in {\mathbb{N}^*}|{x^3} - 8{x^2} + 15x = 0} \right\}\). Số phần tử của tập \(A\) là
\(2\);
\(3\);
\(0\);
\(1\).
Mệnh đề nào dưới đây là đúng?
\(\left( {0;\,\,3} \right] \subset \left( { - 1;\,3} \right)\);
\(\left( { - 1;2} \right) \subset \mathbb{Q}\);
\(\left( { - 1;\,\,4} \right) \cup \left[ {5;\,\,6} \right] \subset \mathbb{Z}\);
\(\left\{ {\frac{1}{2}} \right\} \subset \mathbb{Q}\).
Cho \(A,\,\,B,\,\,C\) là ba tập hợp bất kì khác rỗng, được biểu diễn bằng biểu đồ Ven như hình bên. Phần gạch sọc trong hình vẽ biểu diễn tập hợp nào sau đây?
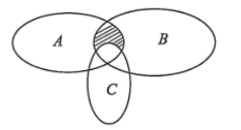
Phần gạch chéo trong hình tương ứng với tập hợp nào sau đây?
\(\left( {A \cup B} \right)\backslash C\);
\(\left( {A \cap B} \right)\backslash C\);
\(\left( {A \cap B} \right) \cap C\);
\(\left( {A \cap B} \right) \cup C\).
Lớp \(10A\) có \(26\)em thích bóng đá, \(30\) em thích bóng chuyền, \(15\) em thích cả bóng đá và bóng chuyền. Hỏi lớp \(10A\) có bao nhiêu học sinh (biết các học sinh của lớp đều thích ít nhất một trong hai môn trên)?
\(56\);
\(71\);
\(41\);
\(45\).
Cho bất phương trình bậc nhất hai ẩn: \(\left( {3m + 2} \right)x - \left( {m - 1} \right)y < 2\). Tìm điều kiện của tham số \(m\) để cặp \(\left( {1;\,\, - 1} \right)\) là nghiệm của bất phương trình đã cho.
\(m \ge \frac{1}{4}\);
\(m < - \frac{1}{2}\);
\(m < \frac{1}{4}\);
\(m > - \frac{1}{2}\).
Anh Trung có kế hoạch đầu tư \(400\) triệu đồng vào hai khoản \(X\) và \(Y\). Để đạt được lợi nhuận thì số tiền đầu tư cho khoản \(X\) phải ít nhất là \(100\) triệu đồng và số tiền đầu tư cho khoản \(Y\) không nhỏ hơn số tiền đầu tư cho khoản \(X\). Viết hệ bất phương trình bậc nhất hai ẩn mô tả về hai khoản đầu tư đó.
\(\left\{ \begin{array}{l}x \ge 0\\x - y \le 10\\y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x \ge 100\\x - y \le 100\\y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x \ge 100\\x - y \le 0\\y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x \ge 100\\x - y \le 10\\y \ge 100\end{array} \right.\).
Bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(x - {12^2}y > 7\);
\(3x + 4{y^2} \le 7\);
\(\frac{2}{x} - 7y > 90\)
\(xy \ge - 9\).
Cho các hệ sau:
(I). \(\left\{ \begin{array}{l}3x + y < 0\\x + 2y > 3\end{array} \right.\); (II). \(\left\{ \begin{array}{l}x - y < 0\\x + 2y \ge 0\end{array} \right.\);
(III). \(\left\{ \begin{array}{l}{x^2} - y > 0\\x + {y^2} \le 0\end{array} \right.\); (IV). \(\left\{ \begin{array}{l}x + \frac{1}{{\sqrt 2 }}y > 0\\\sqrt 2 x - y \le 0\end{array} \right.\).
Số hệ bất phương trình bậc nhất hai ẩn là
\(0\);
\(1\);
\(2\);
\(3\).
Miền không gạch chéo (không kể biên) là miền nghiệm của bất phương trình bậc nhất hai ẩn được biểu diễn bởi hình vẽ sau:
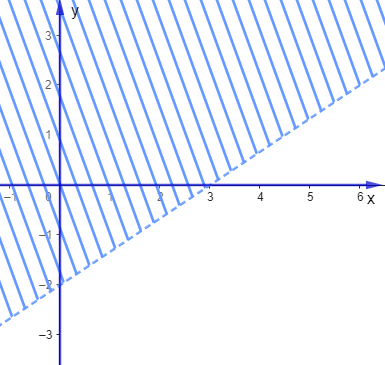
Điểm nào sau đây thuộc miền nghiệm của bất phương trình đã cho?
\(\left( {3;\,\,0} \right)\);
\(\left( {0;\,\, - 2} \right)\);
\((0;\,\,0)\);
\(\left( {5;0} \right)\).
Cho hình vẽ sau:

Miền không bị gạch chéo kể cả đường thẳng \({d_2}\) và không kể đường thẳng \({d_1}\) biểu diễn miền nghiệm của hệ bất phương trình nào dưới đây?
\(\left\{ \begin{array}{l}x - y < - 2\\x + 5y \ge 10\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y \ge 2\\x + 5y < 10\end{array} \right.\);
\(\left\{ \begin{array}{l}x + y \ge - 2\\x - 5y < 10\end{array} \right.\);
\(\left\{ \begin{array}{l}x + y < - 2\\x + 5y \ge 10\end{array} \right.\).
Cho hàm số có đồ thị như hình bên dưới.
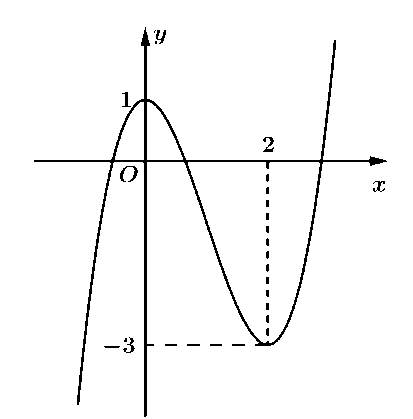
Khẳng định nào sau đây là đúng?
Hàm số nghịch biến trên khoảng \[\left( {0;3} \right)\];
Hàm số đồng biến trên khoảng \[\left( { - \infty ;1} \right)\];
Hàm số nghịch biến trên khoảng \[\left( {0;2} \right)\];
Hàm số đồng biến trên khoảng \[\left( { - \infty ;3} \right)\].
Điều kiện của tham số \(m\) để hàm số \(y = \left( {2m - 3} \right)x + m + 1\) đồng biến trên \(\mathbb{R}\).
\(m < \frac{3}{2}\);
\(m > - \frac{3}{2}\);
\(m \ne \frac{3}{2}\);
\(m > \frac{3}{2}\).
Tập xác định của hàm số \(y = \frac{{4 - x}}{{x + \sqrt {x - 1} }}\) là
\(\left[ {1;\,\, + \infty } \right)\);
\(\left( {1; + \infty } \right)\);
\(\left( { - \infty ; + \infty } \right)\backslash \left\{ 1 \right\}\);
\(\left[ {1; + \infty } \right)\backslash \left\{ {0;1} \right\}\).
Parabol \[\left( P \right):{\rm{ }}y = - 2{x^2} - 6x + 3\] có hoành độ đỉnh là
\[x = - 3\];
\[x = \frac{3}{2}\];
\[x = - \frac{3}{2}\];
\[x = 3\].
Cho bảng biến thiên sau:
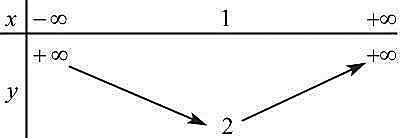
Trục đối xứng của hàm số bậc hai có bảng biến thiên trên là
\(x = 1\);
\(x = 2\);
\(y = 1\);
\(y = 2\).
Cho tam giác \[ABC\] và điểm \[I\] thỏa mãn \[\overrightarrow {IA} = - 2\overrightarrow {IB} \]. Biểu diễn \[\overrightarrow {IC} \] theo các vectơ \[\overrightarrow {AB} \], \[\overrightarrow {AC} \] ta được
\(\overrightarrow {IC} = - 2\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {IC} = 2\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {IC} = - \frac{2}{3}\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {IC} = \frac{2}{3}\overrightarrow {AB} + \overrightarrow {AC} \).
Cho biết \(\tan \alpha = 2\). Giá trị của \(P = \frac{{2\sin \alpha - 2\cos \alpha }}{{2\cos \alpha + 3\sin \alpha }}\) bằng bao nhiêu?
\(P = 0\);
\(P = \frac{1}{4}\);
\(P = - \frac{1}{4}\);
\(P = \frac{2}{7}\).
Cho \(\alpha \) và \(\beta \) thỏa mãn \(0^\circ \le \alpha ,\beta \le 180^\circ \). Phát biểu nào dưới đây là đúng?
Nếu \(\alpha > \beta \) thì \(\tan \alpha > \tan \beta \);
Nếu \(\alpha = - \beta \) thì \[{\rm{cos}}\alpha = {\rm{cos}}\beta \];
Nếu \(\alpha > \beta \) thì \(\sin \alpha = - \sin \beta \);
Nếu \(\alpha = - \beta \) thì \(\cot \alpha = \cot \beta \).
Cho tam giác \(ABC\). Tính \(P = \sin A.\sin \left( {B + C} \right) - \cos A.cos\left( {B + C} \right)\).
\(P = 1\);
\(P = - 1\);
\(P = 2\);
\(P = 0\).
Cho tam giác \[ABC\] với \(BC = a\sqrt 2 \), \(\widehat {BAC} = 150^\circ \). Bán kính đường tròn ngoại tiếp tam giác \[ABC\] là
\(R = \frac{{a\sqrt 2 }}{2}\).
\(R = a\sqrt 3 \).
\(R = a\sqrt 2 \).
\(R = 2a\).
Cho tam giác \(ABC\) có \(AB = 5,\,\,BC = 7,\,\,AC = 8\). Diện tích tam giác \(ABC\) là
\(10\sqrt 3 \);
\(60\sqrt {13} \);
\(280\);
\(10\).
Trong tam giác \(ABC\), phát biểu nào sau đây đúng?
\(\frac{{a + b + c}}{S} = r\);
\(\frac{S}{{a + b + c}} = r\);
\[\frac{S}{{2\left( {a + b + c} \right)}} = r\];
\(\frac{{2S}}{{a + b + c}} = r\).
Giải tam giác là
tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó;
tìm độ dài các cạnh của tam giác;
tìm số đo ba góc của tam giác;
tính diện tích tam giác bằng các cách khác nhau.
Cho tam giác \(ABC\) có \(BC = 16;\,\,\widehat B = 56^\circ ,\,\widehat C = 70^\circ \). Độ dài cạnh \(AC\) xấp xỉ bằng
16,4;
16,3;
16,2;
1\(6\),1.
Chọn khẳng định đúng.
Hai vectơ cùng hướng thì có giá song song;
Hai vectơ cùng phương thì có giá song song;
Hai vectơ cùng hướng thì cùng phương;
Hai vectơ cùng phương thì cùng hướng.
Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?
Diện tích;
Thể tích;
Giá tiền;
Lực.
Cho hình bình hành \(ABCD\). Khẳng định nào sau đây là sai?
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);
\(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \);
\(\overrightarrow {AC} = \overrightarrow {BD} \);
\(\overrightarrow {AB} = \overrightarrow {DC} \).
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Đẳng thức nào sau đây là đúng?
\(\overrightarrow {OA} + \overrightarrow {OB} - \overrightarrow {EO} = \overrightarrow 0 \);
\(\overrightarrow {BC} - \overrightarrow {FE} = \overrightarrow {AD} \);
\(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {EB} - \overrightarrow {OC} \);
\(\overrightarrow {AB} + \overrightarrow {CD} - \overrightarrow {FE} = \overrightarrow 0 \).
Cho hình chữ nhật \(ABCD\) có \(AB = 3a,\,\,AD = a\). Khi đó, \(\left| {\overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {CD} } \right|\) bằng
\(a\sqrt {10} \);
\(4a\);
\(3a\);
\(5a\).
Cho vectơ \(\overrightarrow a \) khác \(\overrightarrow 0 \) và một số thực \(k \ne 0\). Khẳng định nào sau đây là đúng?
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn cùng phương;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn cùng hướng;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) có độ dài bằng nhau;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn ngược hướng.
Cho hình thang \(MNPQ\) có \(MN\,{\rm{//}}\,PQ,\,MN = 2PQ\). Phát biểu nào sau đây là đúng?
\(\overrightarrow {MN} = 2\overrightarrow {PQ} \);
\(\overrightarrow {MQ} = 2\overrightarrow {NP} \);
\(\overrightarrow {MN} = - 2\overrightarrow {PQ} \);
\(\overrightarrow {MQ} = - 2\overrightarrow {NP} \).
Đẳng thức nào sau đây mô tả đúng hình vẽ dưới?

\(\overrightarrow {MP} = \frac{1}{2}\overrightarrow {NP} \);
\(\overrightarrow {MP} = - \frac{1}{2}\overrightarrow {NP} \);
\(\overrightarrow {MN} = 6\overrightarrow {MP} \);
\(\overrightarrow {MN} = 3\overrightarrow {PM} \).
PHẦN II. PHẦN TỰ LUẬN (3 điểm)
(1,0 điểm)
a) Cho hai tập hợp \(A = \left[ { - 9;\,\,5} \right)\) và \(B = \left\{ {x \in \mathbb{R}|x + 2 < 4} \right\}\). Tìm tập hợp \(\left( {{C_\mathbb{R}}A} \right)\backslash B\).
b) Cho tam giác đều \(ABC\) có trọng tâm \(O\). Gọi \(I\) là một điểm tùy ý bên trong tam giác \(ABC\). Hạ \(ID,IE,IF\) tương ứng vuông góc với \(BC,CA,AB\). Tính \(\overrightarrow {ID}+ \overrightarrow {IE}+ \overrightarrow {IF} \) theo vectơ \(\overrightarrow {IO} \).
(1,0 điểm) Anh An làm nghề thợ mộc chuyên đóng bàn và ghế học sinh. Mỗi cái bàn anh bán lãi được \(150\) nghìn đồng, mỗi cái ghế bán lãi được \(100\) nghìn đồng. Mỗi tuần anh làm việc không quá \(60\) giờ. Anh đóng một cái bàn tốn hết \(6\) giờ và đóng một cái ghế tốn hết \(3\) giờ. Để có lãi, anh An phải làm số ghế nhiều hơn số bàn ít nhất \(2\) lần. Hỏi một tuần anh An phải đóng bao nhiêu cái bàn, bao nhiêu cái ghế để số tiền lãi thu về lớn nhất?
(1,0 điểm)
Một tàu đánh cá xuất phát từ cảng \(A\), đi theo hướng \(N60^\circ E\) với vận tốc 60 km/h (\(N60^\circ E\) là hướng tạo với hướng bắc một góc \(60^\circ \) và tạo với hướng đông một góc \(30^\circ \)). Đi được \(90\) phút thì động cơ bị hỏng nên tàu trôi tự do theo hướng bắc với vận tốc 6 km/h. Sau \(3\) giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo. Tính khoảng cách từ cảng \(A\) tới đảo nơi tàu neo đậu.