Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh Diều có đáp án - Đề 5
66 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Một bánh xe có \[72\] răng. Số đo góc (tính theo đơn vị radian) mà bánh xe đã quay được khi di chuyển \[10\] răng là
\(\frac{\pi }{6}\);
\[\frac{\pi }{{36}}\];
\(\frac{{5\pi }}{{18}}\);
\(\frac{\pi }{3}\).
Điểm cuối của góc lượng giác \(\alpha \) ở góc phần tư thứ mấy nếu \({\rm{sin}}\alpha ,{\rm{cos}}\alpha \) cùng dấu?
Thứ II;
Thứ IV;
Thứ II hoặc IV;
Thứ I hoặc III.
Giả sử các biểu thức đều có nghĩa, công thức nào sau đây là sai?
\[{\sin ^2}\alpha + {\cos ^2}\alpha = 1\];
\(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\);
\(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\);
\(\tan \alpha + \cot \alpha = 1\).
Trong mặt phẳng tọa độ \(Oxy,\) trên đường tròn lượng giác gọi điểm \(M\)là điểm biểu diễn của góc \(\alpha = \frac{\pi }{3}\). Lấy điểm \(N\) đối xứng với \(M\) qua trục \[Oy\]. Khi đó \(N\) là điểm biểu diễn của góc có số đo bằng bao nhiêu?
\( - \frac{\pi }{3}\);
\(\frac{{2\pi }}{3}\);
\(\frac{\pi }{6}\);
\(\frac{{4\pi }}{3}\).
Cho góc \(\alpha \) thỏa mãn \({\rm{tan}}\alpha + {\rm{cot}}\alpha = 2\). Giá trị của biểu thức \(P = {\rm{ta}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{t}}^2}\alpha \) là
\(P = 1\);
\(P = 2\);
\(P = 3\);
\(P = 4\).
Rút gọn biểu thức \(M = {\rm{cos}}\left( {a + b} \right){\rm{cos}}\left( {a - b} \right) + {\rm{sin}}\left( {a + b} \right){\rm{sin}}\left( {a - b} \right)\) ta được
\(M = 1 - 2{\rm{si}}{{\rm{n}}^2}b\);
\(M = 1 + 2{\rm{si}}{{\rm{n}}^2}b\);
\(M = 1 - 2{\rm{si}}{{\rm{n}}^2}a\);
\(M = 1 + 2{\rm{si}}{{\rm{n}}^2}a\).
Hàm số \(y = f\left( x \right)\) (có tập xác định \(D\)) là hàm số lẻ nếu với \(\forall x \in D\) thì \( - x \in D\) và
\[f\left( { - x} \right) = f\left( x \right)\];
\[f\left( { - x} \right) = - f\left( x \right)\];
\[f\left( { - x} \right) = f\left( {\pi x} \right)\];
\[f\left( { - x} \right) = - f\left( {\pi x} \right)\].
Trong các hàm số \(y = \sin x\), \(y = \cos x\), \(y = \tan x\), \(y = \cot x\), có bao nhiêu hàm số tuần hoàn chu kì \(2\pi \)?
1;
2;
3;
4.
Hàm số \(y = \cot x\) có đồ thị như hình vẽ.
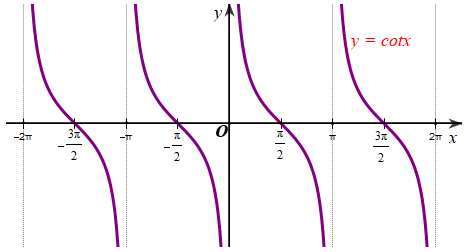
Hàm số \(y = \cot x\) nghịch biến trên khoảng hay đoạn nào dưới đây?
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\);
\(\left[ { - \frac{\pi }{2};0} \right]\);
\(\left( {0;\pi } \right)\);
\(\mathbb{R}\).
Tập xác định \(D\) của hàm số \(y = \sqrt {1 - {\rm{sin}}2x} - \sqrt {1 + {\rm{sin}}2x} \) là
\(D = \emptyset \);
\(D = \mathbb{R}\);
\(D = \left[ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi } \right],k \in \mathbb{Z}\);
\(D = \left[ {\frac{{5\pi }}{6} + k2\pi ;\frac{{13\pi }}{6} + k2\pi } \right],k \in \mathbb{Z}\).
Giá trị nhỏ nhất của hàm số \(y = {\cos ^2}x - 4\cos x - 5\) là
\( - 20\);
\( - 8\);
0;
9.
Phương trình \(\sin x = 0\) có nghiệm là
\(x = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Nghiệm của phương trình \(\cot x = - 1\) là
\(x = - \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = - \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Phương trình \(\cos 2x = \cos \left( {x + \frac{\pi }{3}} \right)\) có nghiệm là
\[x = \frac{\pi }{3} + k2\pi \]; \[x = - \frac{\pi }{9} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\];
\[x = \frac{\pi }{3} + k2\pi \]; \[x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\];
\[x = \pm \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\];
\[x = - \frac{\pi }{9} + k\frac{{2\pi }}{3};x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\].
Có bao nhiêu giá trị \(x \in \left[ {0;3\pi } \right]\) thỏa mãn \(3\tan x - \sqrt 3 = 0\)?
0;
1;
2;
3.
Với \[n \in {\mathbb{N}^*}\], cho dãy số \[\left( {{u_n}} \right)\] có số hạng tổng quát \[{u_n} = {n^2} - 1\]. Năm số hạng đầu tiên của dãy số này là
\( - 1;0;3;8;16\);
\[1;4;9;16;25\];
\(0;3;8;15;24\);
\(0;3;6;9;12\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {2^n}.\) Số hạng \({u_{n + 1}}\) là
\[{u_{n + 1}} = {2^n}.2\];
\[{u_{n + 1}} = {2^n} + 1\];
\[{u_{n + 1}} = 2\left( {n + 1} \right)\];
\[{u_{n + 1}} = {2^n} + 2\].
Trong các dãy số sau, dãy số nào bị chặn dưới?
\[\left( {{u_n}} \right):{u_n} = 4 - n\];
\[\left( {{v_n}} \right):{v_n} = {n^2} - 4n + 5\];
\[\left( {{k_n}} \right):{k_n} = - {n^2} + 3\];
\[\left( {{a_n}} \right):{a_n} = {\left( { - 2} \right)^n}\].
Cho cấp số cộng \(\left( {{u_n}} \right),\) có số hạng đầu bằng \({u_1}\) và công sai bằng \(d.\) Công thức số hạng tổng quát \({u_n}\) là
\({u_n} = {u_1} + nd\);
\({u_n} = {u_1} + \left( {n - 1} \right)d\);
\({u_n} = {u_1} + \left( {n + 1} \right)d\);
\({u_n} = {u_1} + \left( {1 - n} \right)d\).
Dãy số nào sau đây là cấp số cộng?
\(1;3;6;9;12\);
\(1;4;7;10;14\);
\(1;2;4;8;16\);
\(0;4;8;12;16\).
Cho \(\left( {{u_n}} \right)\)là cấp số cộng biết \({u_3} + {u_{13}} = 80\). Tổng 15 số hạng đầu của cấp số cộng đó bằng
\(570\);
\(600\);
\(630\);
\(800\).
Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(b\)?
0;
1;
2;
vô số.
Cho hình chóp \(S.ABC\). Gọi \(M\) là trung điểm của \(SA\), \(N\) là điểm bất kì trên cạnh \(SB\) (\(N\) không trùng với trung điểm và hai đầu mút). Gọi \(I\) là giao điểm của \(MN\) và \(AB\). Điểm \(I\) không nằm trên mặt phẳng nào sau đây?
\(\left( {ABC} \right)\);
\(\left( {SAB} \right)\);
\(\left( {AMNB} \right)\);
\(\left( {SAC} \right)\).
Hình chóp có 16 cạnh thì có bao nhiêu mặt?
7;
8;
9;
10.
Hình chóp \[S.ABC\] có \[SA = SB = SC\] được gọi là
Hình chóp tam giác đều;
Hình tứ diện;
Hình chóp tứ giác;
Cả A, B, C đều sai.
Cho tứ diện \(ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(CD\). Giao tuyến của hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right)\) là
Đường thẳng \(MN\);
Đường thẳng \(AC\);
Đường thẳng \(BG\) (\(G\)là trọng tâm tam giác \(ACD\));
Đường thẳng \(AH\)(\(H\)là trực tâm tam giác \(ACD\)).
Cho tứ diện \(SABC\). Gọi \(L,{\rm{ }}M,{\rm{ }}N\) lần lượt là các điểm trên các cạnh \(SA,{\rm{ }}SB\) và \(AC\) sao cho \(LM\) không song song với \(AB\), \(LN\) không song song với \(SC\). Mặt phẳng \(\left( {LMN} \right)\) cắt các cạnh \(AB,{\rm{ }}BC,{\rm{ }}SC\) lần lượt tại \(K,{\rm{ }}I,{\rm{ }}J\). Ba điểm nào sau đây thẳng hàng?
\(K,{\rm{ }}I,{\rm{ }}J\);
\(M,{\rm{ }}I,{\rm{ }}J\);
\(N,{\rm{ }}I,{\rm{ }}J\);
\(M,{\rm{ }}K,{\rm{ }}J\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào chéo nhau?
\(AB\) và \(CD\);
\(AC\) và \[BD\];
\(SB\) và \(CD\);
\(SD\) và \(BD\).
Cho hai đường thẳng phân biệt \[a\] và \(b\) cùng thuộc mặt phẳng \(\left( \alpha \right).\) Có bao nhiêu vị trí tương đối giữa hai đường thẳng \(a\) và \(b?\)
1;
2;
3;
4.
Khẳng định nào sau đây là sai?
Trong không gian, hai đường thẳng phân biệt cùng song song vơi đường thẳng thứ ba thì chúng song song với nhau;
Có đúng một mặt phẳng chứa hai đường thẳng song song;
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đôi một song song;
Nếu hai mặt phẳng lần lượt chứa hai đường thẳng song song thì giao tuyến nếu có của chúng sẽ song song với hai đường thẳng đó.
Cho tứ diện \(ABCD\), gọi \(G\) và \(E\) lần lượt là trọng tâm của tam giác \(ABD\) và \(ABC\). Mệnh đề nào dưới đây đúng?
\(GE\) và \(CD\) chéo nhau;
\(GE\,{\rm{//}}\,CD\);
\(GE\) và \(AD\)cắt nhau;
\(GE\) và \(CD\) cắt nhau.
Cho hai mặt phẳng \(\left( P \right),\,\left( Q \right)\) cắt nhau theo giao tuyến là đường thẳng \(d\). Đường thẳng \(a\) song song với cả hai mặt phẳng \(\left( P \right),\,\left( Q \right)\). Khẳng định nào sau đây đúng?
\(a,d\) trùng nhau;
\(a,d\) chéo nhau;
\(a\) song song \(d\);
\(a,d\) cắt nhau.
Cho hai đường thẳng song song \(a\) và \(b\). Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(b\)?
Một mặt phẳng;
Hai mặt phẳng;
Vô số mặt phẳng;
Không có mặt phẳng nào.
Cho các giả thiết sau. Giả thiết nào kết luận đường thẳng \(a\) song song với mặt phẳng \(\left( \alpha \right)\)?
\(a\;{\rm{//}}\;b\) và \(b \subset \left( \alpha \right)\);
\(a\;{\rm{//}}\;b\) và \(b\; \cap \;\left( \alpha \right) = \emptyset \);
\(a\;{\rm{//}}\;b\) và \(b\;{\rm{//}}\;\left( \alpha \right)\);
\(a \cap \left( \alpha \right) = \emptyset \).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\), gọi \(I\) là trung điểm cạnh \(SC\). Mệnh đề nào sau đây sai?
Đường thẳng \(IO\) song song với mặt phẳng \(\left( {SAD} \right)\);
Đường thẳng \(IO\) song song với mặt phẳng \(\left( {SAB} \right)\);
Mặt phẳng \(\left( {IBD} \right)\) cắt mặt phẳng \(\left( {SAC} \right)\) theo giao tuyến \(OI\);
Mặt phẳng \(\left( {IBD} \right)\) cắt hình chóp \(S.ABCD\) theo một thiết diện là tứ giác.
PHẦN II. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Giải các phương trình lượng giác:
a) \(4{\sin ^2}x - 12\cos x - 9 = 0\);
b) \(3{\rm{si}}{{\rm{n}}^2}x + \left( {3 - \sqrt 3 } \right){\rm{sin}}x{\rm{cos}}x = \sqrt 3 {\rm{co}}{{\rm{s}}^2}x{\rm{\;}}\).
(1,0 điểm) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Lấy điểm \(M\) trên cạnh \(AD\) sao cho \(AD = 3AM\). Gọi \(G,N\) lần lượt là trọng tâm của tam giác \(SAB,ABC\). Chứng minh rằng \(MN\,{\rm{//}}\,\left( {SCD} \right)\) và \(NG\,{\rm{//}}\,\left( {SAC} \right)\).
(1,0 điểm)Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \(x = 3\cos \left( {4\pi t - \frac{{2\pi }}{3}} \right)\), với \(t\) là thời gian tính bằng giây và \(x\) là quãng đường tính bằng \[{\rm{cm}}\]. Hãy cho biết trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
I. TRẮC NGHIỆM (7 ĐIỂM)
Câu nào dưới đây là mệnh đề Toán học?
\(2\) chia hết cho \(3\);
Hôm nay là thứ mấy?
Việt Nam có 63 tỉnh thành;
Đề thi Toán thật khó!.
Cho mệnh đề \(P\): “Tứ giác \(ABCD\) là hình thang cân” và mệnh đề \(Q\): “Tứ giác \(ABCD\) có \(AC = BD\)”. Mệnh đề \(P \Rightarrow Q\) được phát biểu là
Tứ giác \(ABCD\) là hình thang cân vì tứ giác \(ABCD\) có \(AC = BD\);
Nếu tứ giác \(ABCD\) là hình thang cân do đó tứ giác \(ABCD\) có \(AC = BD\); ;
Nếu tứ giác \(ABCD\) là hình thang cân thì tứ giác \(ABCD\) có \(AC = BD\);
Tứ giác \(ABCD\) có \(AC = BD\) khi và chỉ khi tứ giác \(ABCD\) là hình thang cân.
Mệnh đề “\(\exists x \in \mathbb{Z},x\,\, \vdots \,\,5\)” được diễn tả bằng lời là
Tồn tại một số nguyên \(x\) để \(x\) chia hết cho 5;
Mọi số nguyên \(x\) chia hết cho 5;
Tồn tại một số nguyên \(x\) để \(x\) không chia hết cho 5;
Mọi số nguyên \(x\) không chia hết cho 5.
Cho định lí: “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ” để phát biểu lại định lí. Khẳng định nào sau đây là đúng ?
Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau;
Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau;
Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau;
Hai tam giác có diện tích bằng nhau là điều kiện cần và đủ để chúng bằng nhau.
Cho tập hợp \(X = \){\(x \in \mathbb{N}|x\)là ước của \(18\) và \(12\)}. Số tập con khác rỗng của tập \(X\) là
\(4\);
\(15\);
\(16\);
\(14\).
Cho tập hợp \(B = \left\{ {x \in \mathbb{R}|5 < x < 50} \right\}\). Khoảng nào sau đây là tập con của \(B\) ?
\(\left( { - 1;6} \right)\)
\(\left( {45;69} \right)\);
\(\left( {23;34} \right)\);
\(\left( {1;50} \right)\).
Cho các tập hợp sau: \(A\) = {\(x|x\) là hình bình hành}, \(B\) = {\(x|x\) là hình chữ nhật}, \(C\) = {\(x|x\) là hình thoi}, \(D\) = {\(x|x\) là hình vuông}. Mệnh đề nào sau đây sai?
\(B \cap C = D\);
\(C \cap D = D\);
\(B \cup C = D\);
\(B \cap D = D\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}|{x^2} - 2x + 1 = 0} \right\}\). Trong các phần tử sau, phần tử nào thuộc tập hợp \(A\)?
1;
2;
– 1;
0.
Cho biểu thức \(F\left( {x;\,\,y} \right) = x - 2y + 1\) với \(\left( {x;\,y} \right)\) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l} - x - 2y \ge - 10\\2x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\). Biểu thức \(F\left( {x;\,\,y} \right)\) đạt giá trị nhỏ nhất tại cặp \(\left( {x;\,y} \right)\) có giá trị là
\(\left( {0;\,\,5} \right)\);
\(\left( {0;\,\,0} \right)\);
\(\left( {2;\,\,4} \right)\);
\(\left( {4;\,\,0} \right)\).
Bất phương trình nào dưới đây không phải là bất phương trình bậc nhất hai ẩn?
\(x - y \ge 8\);
\(3x + 7y < 0\);
\(4x > - 3\);
\(x - y + z < 1\).
Lan muốn đống góp quà trung thu cho các cháu thiếu nhi bằng cách mua \(2\) loại kẹo từ số tiền tiết kiệm \(350\,\,000\)đồng của mình. Biết kẹo hương dâu giá \(32\,\,000\)đồng/ hộp, kẹo hương cam giá \(36\,\,000\)đồng/hộp. Lan đã mua \(x\) hộp kẹo hương dâu và \(y\) hộp kẹo hương cam. Bất phương trình nào sau đây mô tả điều kiện ràng buộc với \(x,y\)?
\(x + y \ge 35\);
\(32x + 36y \ge 350\);
\(32x + 36y \le 350\);
\(36x + 32y \le 350\).
Miền nghiệm của bất phương trình bậc nhất hai ẩn \(3x - y \ge 1\) là
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) không chứa điểm \(\left( {0;0} \right)\) (không kể bờ);
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) chứa điểm \(\left( {0;0} \right)\) (có kể bờ);
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) không chứa điểm \(\left( {0;0} \right)\) (có kể bờ);
Nửa mặt phẳng có bờ là đường thẳng \(3x - y = 1\) không chứa điểm \(\left( {0;0} \right)\)(không kể bờ).
Cặp số nào sau đây là nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}5x - 2y \le 0\\x + y < 10\end{array} \right.\) ?
\(\left( {1;2} \right)\);
\(\left( {4;5} \right)\);
\(\left( {10;30} \right)\);
\(\left( { - 5;10} \right)\).
Trong các hệ bất phương trình sau, hệ bất phương trình bậc nhất hai ẩn là
\(\left\{ \begin{array}{l}{x^2} - {y^2} > 4\\2x + y < 1\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^2} - 2y \le z\\x + y < 9\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^5} - y > 0\\x + {y^5} < 6\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y - 3 > 4\\2x + y + 2 < 19\end{array} \right.\).
Cho \[\sin x + {\rm{cos}}x = m\left( { - 1 \le m \le 1} \right)\]. Tính giá trị của biểu thức \(M = \sin x\,.\,{\rm{cos}}x\).
\(M = \frac{{{m^2} + 1}}{2}\);
\(\frac{{{m^2} - 1}}{2}\);
\({m^2} - 1\);
\({m^2} + 1\).
Cho góc \(\alpha \) biết \(0^\circ \le \alpha \le 180^\circ \). Tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} = \alpha \). Khi đó, giá trị \(\cos \alpha \) bằng
\(\frac{{AB}}{{AC}}\);
\(\frac{{AB}}{{BC}}\);
\(\frac{{AC}}{{BC}}\);
\(\frac{{AC}}{{AB}}\).
Mệnh đề nào dưới đây là đúng?
\(\sin x + {\rm{cos}}x = 1\);
\(1 + {\sin ^2}x = \frac{1}{{{{\cot }^2}x}}\);
\({\tan ^2}x + 1 = \frac{1}{{{{\cos }^2}x}}\);
\[\tan x = \frac{{{\rm{cos}}\,x}}{{{\mathop{\rm s}\nolimits} {\rm{in}}\,x}}\].
Giá trị của biểu thức \(M = {\sin ^2}37^\circ + \tan 67^\circ .\tan 23^\circ + {\rm{co}}{{\rm{s}}^2}143^\circ \) bằng
\(M = 1\);
\(M = 2\);
\(M = - 1\);
\(M = - 2\).
Cho tam giác \(MNP\) có \(MN = 8\,\)cm, \(PN = 5\,\)cm, \(MP = 9\)cm. Vậy \(\widehat {MPN} = ?\) (làm tròn đến độ)
\(45^\circ \);
\(62^\circ \);
\(63^\circ \);
\(48^\circ \).
Công thức heron tính diện tích tam giác \(ABC\) là
\(S = pr\);
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \);
\(S = \frac{1}{2}.a.b.\sin C = \frac{1}{2}.b.c.\sin A\);
\(S = \frac{{abc}}{{4R}}\).
Cho tam giác \(MNP\) có \(MN = 4\,\,{\rm{cm}}\), \(MP = 5\,\,{\rm{cm}}\), \(\widehat {MPN} = 45^\circ \). Làm tròn đến độ ta được số đo \(\widehat {MNP}\) bằng
\(62^\circ \);
\(63^\circ \);
\(64^\circ \);
\(65^\circ \).
Cho hình vuông \(ABCD\) có cạnh bằng \(a\). Gọi \(E\) là trung điểm cạnh \(BC\) và \(F\) là trung điểm cạnh \(AE\). Tính độ dài đoạn thẳng \(DF\).
\(DF = \frac{{a\sqrt {13} }}{4}\);
\(DF = \frac{{a\sqrt 5 }}{4}\);
\(DF = \frac{{a\sqrt 3 }}{2}\);
\(DF = \frac{{3a}}{4}\).
Cho đoạn thẳng \(AB\) có trung điểm \(I\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} \) và \(\overrightarrow {BI} \) cùng hướng;
\(\overrightarrow {AB} \) và \(\overrightarrow {AI} \) cùng hướng;
\(\overrightarrow {AI} \) và \(\overrightarrow {IB} \) ngược hướng;
\(\overrightarrow {AI} \) và \(\overrightarrow {BI} \) không cùng phương.
Cho hình chữ nhật \(ABCD\). Vectơ \(\overrightarrow {AC} \) bằng vectơ nào có điểm đầu và điểm cuối là các đỉnh của hình bình hành?
\(\overrightarrow {BD} \);
\(\overrightarrow {DB} \);
\(\overrightarrow {CA} \);
Không có vectơ nào.
Cho vectơ \(\overrightarrow {AB} \) khác vectơ – không, biết \(A\) và \(B\) nằm trên đường thẳng \(d\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} \) có điểm đầu là \(A\) và không có điểm cuối;
\(\overrightarrow {AB} \) có điểm đầu là \(A\) và điểm cuối là \(B\);
\(\overrightarrow {AB} \) có điểm đầu là \(B\) và điểm cuối là \(A\);
\(\overrightarrow {AB} \) có giá là đường thẳng vuông góc với đường thẳng \(d\).
II. TỰ LUẬN (3 ĐIỂM)
(1 điểm) Trong một cuộc thi làm bánh, mỗi đội chơi được sử dụng tối đa 20 kg bột mì, 2 kg bột nở, 5 kg kem béo. Để làm một cái bánh cỡ bé cần 0,4 kg bột mì, 0,05 kg bột nở và 0,1 kg kem béo; để làm một cái bánh cỡ trung bình 0,6 kg bột mì, 0,075 kg bột nở và 0,15 kg kem béo. Mỗi cái bánh cỡ bé được 5 điểm thưởng, mỗi cái bánh cỡ lớn được 7 điểm thưởng. Hỏi cần phải làm mấy cái bánh mỗi loại để được nhiều điểm thưởng nhất?
(1,0 điểm)
a) Kí hiệu \(H\) là tập hợp học sinh lớp 10A1, \(T\) là tập hợp các học sinh nam và \(G\) là tập hợp các học sinh nữ của lớp 10A1. Hãy các định các tập hợp \(T \cup G,\,\,T \cap G\) và \(H\backslash T\).
b) Cho các tập hợp
\(A = \left\{ {x \in \mathbb{Z}|\left( {x + 2} \right)\left( {5{x^2} - 6x + 1} \right) = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{R}|{x^2} - \left( {2m + 1} \right)x + 2m = 0} \right\}\).
Tìm điều kiện của tham số m để \(A \cup B\) có đúng 3 phần tử và tổng bình phương của chúng bằng 9.
(1 điểm) Đường dây cao thế nối thẳng từ vị trí \(A\) đến vị trí \(B\) dài 15 km, từ vị trí \(A\) đến vị trí \(C\) dài 9 km, góc tạo bởi hai đường dây trên bằng \(86^\circ \). Tính khoảng cách từ vị trí \(B\) đến vị trí \(C\) (h.57). (làm tròn kết quả đến hàng phần trăm)