Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh Diều có đáp án - Đề 2
66 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Nếu một góc lượng giác có số đo bằng radian là \(\frac{{5\pi }}{4}\) thì số đo bằng độ của góc lượng giác đó là
\({5^{\rm{o}}}\);
\({15^{\rm{o}}}\);
\({172^{\rm{o}}}\);
\({225^{\rm{o}}}\).
Trong mặt phẳng tọa độ \(Oxy,\)cho đường tròn lượng giác như hình vẽ bên dưới.
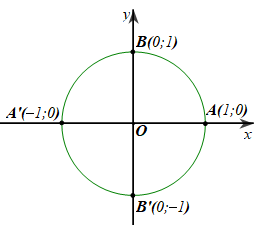
Hỏi góc lượng giác nào sau đây có số đo là \( - 90^\circ \)?
\(\left( {OA,OB} \right)\);
\(\left( {OA,OA'} \right)\);
\(\left( {OA,OB'} \right)\);
\(\left( {OA,OA} \right)\).
Mệnh đề nào sau đây là sai?
\( - 1 \le {\rm{sin}}\alpha \le 1; - 1 \le {\rm{cos}}\alpha \le 1\);
\({\rm{tan}}\alpha = \frac{{{\rm{sin}}\alpha }}{{{\rm{cos}}\alpha }}\left( {{\rm{cos}}\alpha \ne 0} \right)\);
\({\rm{si}}{{\rm{n}}^2}\left( {2\alpha } \right) + {\rm{co}}{{\rm{s}}^2}\left( {2\alpha } \right) = 2\).
Cho \({\rm{cos}}\alpha = \frac{1}{3}\). Khi đó \({\rm{sin}}\left( {\alpha - \frac{{3\pi }}{2}} \right)\) bằng
\( - \frac{2}{3}\);
\( - \frac{1}{3}\);
\(\frac{1}{3}\);
\(\frac{2}{3}\).
Cho góc \(\alpha \) thỏa mãn \({\rm{sin}}\alpha = \frac{{12}}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \). Giá trị của \({\rm{cos}}\alpha \) là
\({\rm{cos}}\alpha = \frac{1}{{13}}\);
\({\rm{cos}}\alpha = \frac{5}{{13}}\);
\({\rm{cos}}\alpha = - \frac{5}{{13}}\);
\({\rm{cos}}\alpha = - \frac{1}{{13}}\).
Khẳng định nào sau đây đúng?
\({\rm{sin}}\left( {2030a} \right) = 2030{\rm{sin}}a.{\rm{cos}}a\);
\({\rm{sin}}\left( {2030a} \right) = 2030{\rm{sin}}\left( {1015a} \right){\rm{.cos}}\left( {1015a} \right)\);
\({\rm{sin}}\left( {2030a} \right) = 2{\rm{sin}}a{\rm{cos}}a\);
\({\rm{sin}}\left( {2030a} \right) = 2{\rm{sin}}\left( {1015a} \right){\rm{.cos}}\left( {1015a} \right)\).
Trong các hàm số \(y = \sin x\), \(y = \cos x\), \(y = \tan x\), \(y = \cot x\), có bao nhiêu hàm số có đồ thị đối xứng qua gốc tọa độ?
0;
1;
2;
3.
Hàm số \(y = \sin x\) là hàm số tuần hoàn với chu kì
\(\pi \);
\(2\pi \);
\(\frac{1}{2}\pi \);
\(3\pi \).
Cho hàm số \(y = \cos x\) có đồ thị như hình vẽ dưới đây:
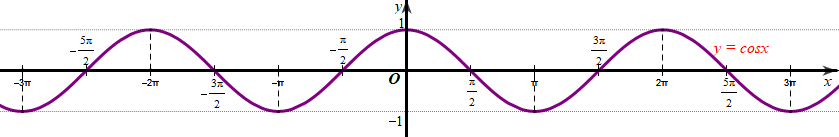
Hàm số \(y = \cos x\) đồng biến trên khoảng nào?
\(\left( {0;\pi } \right)\);
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\);
\(\left( { - 3\pi ; - 2\pi } \right)\);
\(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
Tập xác định \(D\) của hàm số \(y = \sqrt {{\rm{sin}}x + 2} \) là
\(D = \mathbb{R}\);
\(D = \left[ { - 2; + \infty } \right)\);
\(D = \left[ {0;2\pi } \right]\);
\(D = \emptyset \).
Tập giá trị \(T\) của hàm số \[y = 5 - 3\sin x\] là
\(T = \left[ { - 1;1} \right]\);
\(T = \left[ { - 3;3} \right]\);
\(T = \left[ {2;8} \right]\);
\(T = \left[ {5;8} \right]\).
Tất cả nghiệm của phương trình \(\tan x = \tan \frac{\pi }{{11}}\) là
\(x = \frac{\pi }{{11}} + k2\pi ,k \in \mathbb{Z}\);
\(x = \frac{\pi }{{11}} + k\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{{11}} + k2\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{{11}} + k\pi ,k \in \mathbb{Z}\).
Nghiệm của phương trình \(\cos \frac{x}{2} = 1\) là
\(x = k2\pi ,k \in \mathbb{Z}\);
\(x = k\pi ,k \in \mathbb{Z}\);
\(x = \pi + k2\pi ,k \in \mathbb{Z}\);
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\).
Giá trị của tham số \(m\) để phương trình \(\sin x - m = 0\) có nghiệm là
\(m \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\);
\(m \in \left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\);
\(m \in \left[ { - 1;1} \right]\);
\(m \in \left( { - 1;1} \right)\).
Nghiệm của phương trình \(\cot \left( {\frac{x}{2} + \frac{\pi }{4}} \right) = - 1\) là
\(x = - \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\);
\(x = - \pi + k\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\);
\(x = - \pi + k2\pi ,k \in \mathbb{Z}\).
Dãy số nào dưới đây là dãy số nguyên tố nhỏ hơn \[10\] theo thứ tự tăng dần?
\(0;1;2;3;5;7\);
\(1;2;3;5;7\);
\(2;3;5;7\);
\(1;3;5;7\).
Với \[n \in {\mathbb{N}^*}\], trong các dãy số \(\left( {{u_n}} \right)\) cho bởi số hạng tổng quát \({u_n}\) sau, dãy số nào là dãy số tăng?
\[{u_n} = \frac{2}{{{3^n}}}\];
\[{u_n} = \frac{3}{n}\];
\[{u_n} = {2^n}\];
\[{u_n} = {\left( { - 2} \right)^n}\].
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_n} = - {n^2} + n + 1\). Số \( - 19\) là số hạng thứ mấy của dãy?
4;
5;
6;
7.
Trong các dãy số sau, dãy số nào là một cấp số cộng?
\(1; - 2; - 4; - 6; - 8\);
\(1; - 3; - 6; - 9; - 12\);
\(1; - 3; - 7; - 11; - 15\);
\(1; - 3; - 5; - 7; - 9\).
Cho cấp số cộng \(\left( {{u_n}} \right)\)có \({u_1} = - 0,1\) và \(d = 0,1\). Số hạng thứ \(7\)của cấp số cộng là
\(0,5\);
\(0,6\);
\(1,6\);
\(6\).
Tổng của bao nhiêu số hạng đầu của cấp số cộng \(1; - 1; - 3;...\) bằng \( - 9800\)?
98;
99;
100;
101.
Cho bốn điểm \(A,\,B,\,C,\,D\) không cùng nằm trong một mặt phẳng. Trên \(AB,\,AD\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \(MN\) cắt \(BD\) tại \(I\). Điểm \(I\) không thuộc mặt phẳng nào sao đây?
\[\left( {BCD} \right)\];
\[\left( {ABD} \right)\];
\[\left( {CMN} \right)\];
\[\left( {ACD} \right)\].
Cho hai đường thẳng \(a,b\) cắt nhau và không đi qua điểm \(A\). Xác định được nhiều nhất bao nhiêu mặt phẳng bởi \(a,b\) và \(A\)?
1;
2;
3;
4.
Hình chóp lục giác có bao nhiêu mặt bên?
4;
5;
6;
7.
Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
2;
3;
4;
6.
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AD,BC\), điểm \(G\) là trọng tâm của tam giác \(BCD\). Giao điểm của đường thẳng \(MG\) với mặt phẳng \(\left( {ABC} \right)\) là
giao điểm của \(MG\) và \(BC\);
giao điểm của \(MG\) và \(AC\);
giao điểm của \(MG\) và \(AN\);
giao điểm của \(MG\) và \(AB\).
Cho hình chóp \[S.ABCD\], có \[ABCD\] là tứ giác không có cặp cạnh đối nào song song, \[M\] là trung điểm \[SA\]. Gọi \[I\] là giao điểm của \[AB\] và \[CD\], \[K\] là giao điểm của \[AD\] và \[CB\]. Giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {MCD} \right)\] là
\(MI\);
\(MK\);
\(IK\);
\(SI\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Hỏi cạnh \[CD\] chéo với tất cả các cạnh nào của hình chóp?
\[SA;\,AB\];
\[SA;\,SB\];
\[SB;AB\];
\[SB;\,AD\].
Khẳng định nào sau đây là đúng?
Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau;
Hai đường thẳng phân biệt không cắt nhau thì chéo nhau;
Hai đường thẳng phân biệt không song song thì chéo nhau;
Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
Cho tứ diện \(ABCD\). Gọi \(I,J\) lần lượt là trọng tâm các tam giác \(ABC\) và \(ABD\). Khẳng định nào sau đây là đúng?
\[IJ\] song song với \(CD\);
\[IJ\] song song với \(AB\);
\[IJ\] chéo \(CD\);
\[IJ\] cắt \(AB\).
Cho hình chóp \[S.ABCD\] có đáy \(ABCD\) là hình bình hành. Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\). Khẳng định nào sau đây đúng?
\(d\) qua \(S\) và song song với \(BC\);
\(d\) qua \(S\) và song song với \(DC\);
\(d\) qua \(S\) và song song với \(AB\);
\(d\) qua \(S\) và song song với \(BD\).
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) trong không gian. Có bao nhiêu vị trí tương đối của \(a\) và \(\left( P \right)\)?
1;
2;
3;
4.
Trong không gian, cho đường thẳng \(d\) song song với mặt phẳng \(\left( \alpha \right)\), mặt phẳng \(\left( \beta \right)\) qua \(d\) cắt \(\left( \alpha \right)\) theo giao tuyến \(d'\). Khi đó
\(d\,{\rm{//}}\,d'\);
\(d\) cắt \(d'\);
\(d\) và \(d'\) chéo nhau;
\(d \equiv d'\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, đáy lớn \(AB\). Gọi \(P,Q\) lần lượt là hai điểm nằm trên cạnh \(SA\) và \(SB\) sao cho \(\frac{{SP}}{{SA}} = \frac{{SQ}}{{SB}} = \frac{1}{3}\). Khẳng định nào sau đây là đúng?
\(PQ\) cắt \(\left( {ABCD} \right)\);
\(PQ \subset \left( {ABCD} \right)\);
\(PQ\,{\rm{//}}\,\left( {ABCD} \right)\);
\(PQ\) và \(CD\) chéo nhau.
Cho tứ diện \(ABCD\), gọi \({G_1},{G_2}\) lần lượt là trọng tâm tam giác \(BCD\) và \(ACD.\) Mệnh đề nào sau đây sai?
\({G_1}{G_2}\,{\rm{//}}\,\left( {ABD} \right)\);
Ba đường thẳng \(B{G_1},A{G_2}\) và \(CD\)đồng quy;
\({G_1}{G_2}\,{\rm{//}}\,\left( {ABC} \right)\);
\({G_1}{G_2} = \frac{2}{3}AB\).
PHẦN II. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Giải các phương trình lượng giác:
a) \(\sin \left( {2x + \frac{\pi }{4}} \right) + \cos x = 0\); b) \(\frac{3}{{{{\cos }^2}x}} - 2\sqrt 3 \tan x - 6 = 0\).
(1,0 điểm) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang (hai đáy \(AB > CD\)). Gọi \(M,N\) lần lượt là trung điểm của \(SA,SB\).
a) Tìm giao điểm \(P\) của \(SC\) và mp\(\left( {ADN} \right)\).
b) Biết \(AN\) cắt \(DP\) tại \(I\). Chứng minh \(SI\,{\rm{//}}\,AB\). Tứ giác \(SABI\) là hình gì?
(1,0 điểm)Cho phương trình \(\left( {2\sin x - 1} \right)\left( {3\cos 2x + 2\sin x - m} \right) = 3 - 4{\cos ^2}x\). Tìm tất cả các giá trị của tham số \(m\) để phương trình có đúng ba nghiệm phân biệt trên đoạn \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\).
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Trong các mệnh đề sau mệnh đề nào là mệnh đề sai?
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \]Tam giác \[ABC\] cân;
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \]Tam giác \[ABC\] cân và có một góc \[60^\circ \];
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \]Tam giác \[ABC\] có ba cạnh bằng nhau;
Tam giác \[ABC\] là tam giác đều \[ \Leftrightarrow \] Tam giác \[ABC\] có hai góc bằng \[60^\circ \].
Trong các câu sau, câu nào không phải là mệnh đề?
“Tam giác có hai cạnh bằng nhau là tam giác cân.”;
“Số 100 là một hợp số.”;
“Số 2 022 có chia hết cho 4 không?”;
“Phương trình bậc nhất luôn có nghiệm.”.
Mệnh đề nào sau đây đúng?
Nếu \(a \ge b\) thì \({a^2} \ge {b^2}\);
Nếu \(a\) chia hết cho \(3\) thì \(a\) chia hết cho \(9\);
Nếu tam giác có một góc bằng \(60^\circ \) thì tam giác đó là tam giác đều;
Tổng hai cạnh của một tam giác lớn hơn cạnh còn lại.
Trong các câu sau câu nào là mệnh đề đúng?
\[\sqrt 2 \] là số vô tỉ;
\[5 + 3 < 7\];
\[100\]tỉ là số nguyên lớn nhất;
Trời hôm nay đẹp quá!.
Cho tập hợp\[B = \left\{ {x \in \mathbb{Z}|{x^2} - 4 = 0} \right\}\]. Tập hợp nào sau đây đúng?
\[B = \left\{ {2;{\rm{ }}4} \right\}\];
\[B = \left\{ { - 2;{\rm{ }}4} \right\}\];
\[B = \left\{ { - 4;{\rm{ }}4} \right\}\];
\[B = \left\{ { - 2;{\rm{ 2}}} \right\}\].
Cho tập hợp \(A = \left\{ {1;\,2;\,3} \right\}\). Tập nào sau đây không phải tập con của tập \(A\).
\(\left\{ {12;\,3} \right\}\);
\(\emptyset \);
\(\left\{ {1;\,2} \right\}\);
\(\left\{ {1;\,2;\,3} \right\}\).
Cho hai tập hợp \[P = \{ 1;\,3;\,5;\,7;\,9\} \]và \[Q = \{ 0;\,2;\,4;\,5;\,6;\,8\} \]. Số phần tử của tập hợp \[P \cup Q\]là:
\[0\];
\[1\];
\[10\];
\[11\].
Cho tập hợp \(A = \left\{ {0;\,1;\,2;\,3;\,4} \right\}\) và \(B = \left\{ {2;\,3;\,4;\,5;\,6} \right\}\). Tập hợp \(\left( {A\backslash B} \right) \cap \left( {B\backslash A} \right)\) bằng
\(\left\{ {0;\,1;\,5;\,6} \right\}\);
\(\left\{ {1;\,2} \right\}\);
\(\left\{ {2;\,3;\,4} \right\}\);
\(\emptyset \).
Cho hệ bất phương trình \[\left\{ \begin{array}{l}x + 3y - 2 \ge 0\\2x + y + 1 \le 0\end{array} \right.\]. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
\[M\left( {0;\,1} \right)\];
\[N\left( { - 1;\,1} \right)\];
\[P\left( {1;\,3} \right)\];
\[Q\left( { - 1;\,0} \right)\].
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\[2\left( {x - 1} \right) + 3\left( {y - 2} \right) > 5\];
\(x - y(2y + 1) \le - 3\);
\(2\left( {x - 1} \right) - 2x + 4\sqrt y < 2\);
\(2x\left( {x + 3} \right) - y \le 2\).
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (kể cả đường thẳng d)?
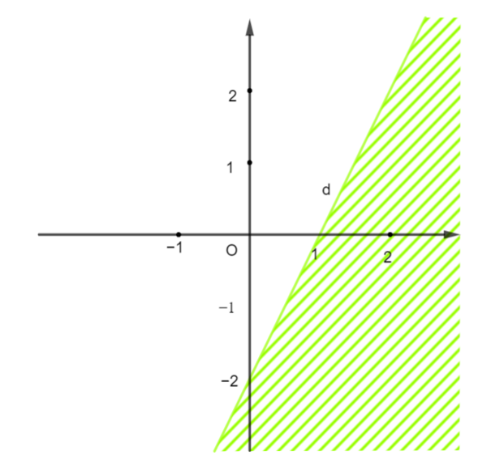
\[2x - y \le 2\];
\[2x - 3y \le 0\];
\[2x + y < 2\];
\[2x - y > 2\].
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
\[\left\{ \begin{array}{l}x + y > x - 3\\x + y < 4\end{array} \right.\];
\(\left\{ \begin{array}{l}{x^2} - y \ge 1\\2x - 4y < 2x - 1\end{array} \right.\);
\[\left\{ \begin{array}{l}x + y + z > 0\\2y - 4 < 0\end{array} \right.\];
\(\left\{ \begin{array}{l}{x^2} \ge 0\\x - 3{y^2} + 4 < 0\end{array} \right.\) .
Phần không gạch trong hình vẽ (không kể biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
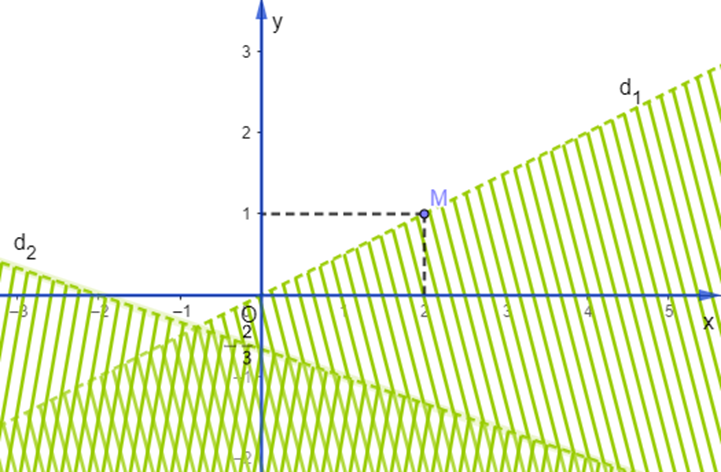
\[\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \ge - 2\end{array} \right.\];
\[\left\{ \begin{array}{l}x - 2y > 0\\x + 3y < - 2\end{array} \right.\];
\[\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \le - 2\end{array} \right.\];
\[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\end{array} \right.\].
Điểm \[A\left( { - 1;\,3} \right)\] là điểm thuộc miền nghiệm của bất phương trình:
\[ - 3x + 2y - 4 > 0\];
\[x + 3y < 0\];
\[3x - y > 0\];
\[2x - y + 4 > 0\].
Trong tam giác \[ABC\]. Khẳng định nào sau đây là đúng?
\[sinA = sin\left( {B + C} \right)\];
\[cosA = cos\left( {B + C} \right)\];
\[cosA > 0\];
\[sinA \le 0\].
Cho \(0^\circ \le \alpha \le 180^\circ \). Khẳng định nào sau đây sai?
\(\tan \left( {180^\circ - \alpha } \right) = - \tan \alpha \left( {\alpha \ne 90^\circ } \right)\);
\({\rm{cos}}\left( {180^\circ - \alpha } \right) = {\rm{cos}}\alpha \);
\(\cot \left( {180^\circ - \alpha } \right) = - \cot \alpha \left( {0^\circ < \alpha < 180^\circ } \right)\).
\(\sin \left( {180^\circ - \alpha } \right) = \sin \alpha \).
Cho tam giác \[ABC\] có các cạnh \[AB = c;{\rm{ }}BC = a;{\rm{ }}AC = b\]. Tính góc \[\widehat {BCA}\] của tam giác \[ABC\] biết \[a \ne b\] và ?
\[\widehat {BCA} = 120^\circ \];
\[\widehat {BCA} = 60^\circ \];
\[\widehat {BCA} = 30^\circ \];
\[\widehat {BCA} = 135^\circ \].
Cho tam giác \(ABC\) với \(p\) là nửa chu vi và \(AB = c;\,BC = a;\,AC = b\). Kết luận nào sau đây sai?
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\);
\(b = \frac{{c.\sin B}}{{\sin C}}\);
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) ;
\(S = ab.\sin C\).
Cho tam giác \[ABC\] đều cạnh \[2a\], bán kính đường tròn nội tiếp tam giác \[ABC\] là:
\[\frac{a}{{\sqrt 3 }}\];
\[\frac{{3a}}{{\sqrt 3 }}\];
\[\frac{{5a}}{{\sqrt 3 }}\];
\[\frac{{7a}}{{\sqrt 3 }}\].
Cho góc \[\alpha \] thỏa mãn \[\sin \alpha + \cos \alpha = \sqrt 2 \]. Giá trị của \[\tan \alpha + \cot \alpha \]là:
\[1\];
\[ - 2\]\[;\]
\[0\]\[;\]
\[2\].
Giả sử \(CD = h\)là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,B\) trên mặt đất sao cho ba điểm \(A,\,B,\,C\) thẳng hàng. Ta đo được \(AB = 24m\)\(\widehat {CAD} = 63^\circ \); \(\widehat {CBD} = 48^\circ \). Chiều cao \(h\) của khối tháp gần với giá trị nào sau đây?
\(61,4m\);
\(18,5m\);
\(62,3m\);
\(18m\).
Cho tam giác \(ABC\) có \(AB = 3,\,\,AC = 6\) và \(\widehat A = 60^\circ \). Bán kính của đường tròn ngoại tiếp tam giác là
3;
\(\sqrt 3 \);
\(3\sqrt 3 \);
\(6\).
Cho hình lục giác đều \(ABCDEF\) tâm \(O\). Số các vectơ khác vectơ không, cùng phương với vectơ \(\overrightarrow {OB} \) có điểm đầu và điểm cuối là các đỉnh của lục giác là
4;
6;
8;
10.
Hình bình hành \[ABCD\] là một hình chữ nhật nếu nó thỏa mãn điều kiện nào trong các điều kiện sau đây?
\[\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BC} } \right|\];
\[\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\];
\[\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right|\];
\[\overrightarrow {AC} = \overrightarrow {BD} \].
Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) được gọi là bằng nhau khi và chỉ khi:
\(AB\parallel CD\) và \(AB = CD\);
\(AB\) trùng \(CD\) và \(AB = CD\);
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng và \(AB = CD\);
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng và \(AB = CD\).
II. PHẦN TỰ LUẬN (3 ĐIỂM)
(1,0 điểm) Cho tập hợp \[C = \left[ { - 3;\,8} \right]\] và \[D = \left[ {m - 3;\,8} \right]\].
a) Cho tập hợp \[A = \left( { - \infty ;\, - 3} \right]\] và \[A\backslash C = B\]. Tìm \[B\].
b) Với giá trị nào của m thì \[C \cap D\] là một đoạn thẳng có độ dài bằng 4.
(1,0 điểm) Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới với vốn đầu tư không quá \[72\] triệu đồng. Loài dài tay mua vào \[800.000\] đồng và lãi \[150.000\]một áo, loại ngắn tay mua vào \[600.000\] đồng và lãi \[120.000\]một áo. Cửa hàng ước tính nhu cầu của khách không quá 100 cái cho cả 2 loại. Lập phương án kinh doanh sao cho lãi nhất.
(1 điểm) Hai chiếc tàu thủy \(P\) và \[Q\] cách nhau 300 m và thẳng hàng với chân \(B\) của tháp hải đăng \(AB\) ở trên bờ biển (hình bên). Từ \(P\) và \(Q,\) người ta nhìn thấy tháp hải đăng \(AB\) dưới các góc \(\widehat {BPA} = 35^\circ \) và \(\widehat {BQA} = 48^\circ \). Tính chiều cao (làm tròn đến hàng phần trăm) của tháp hải đăng đó.
![Hai chiếc tàu thủy \(P\) và \[Q\] các (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/11-1763123464.png)








