Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 08
18 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Trong các cặp số sau, cặp số nào là nghiệm phương trình 
?
Giá trị 
là nghiệm của bất phương trình nào dưới đây?
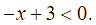
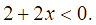
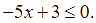
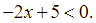
Cho tam giác 
vuông tại 
. Hệ thức nào dưới đây là đúng?
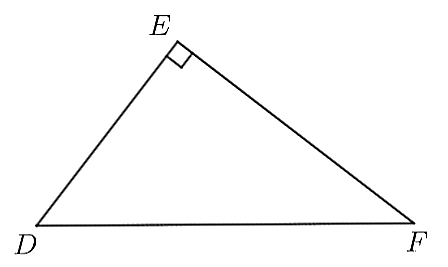
Hai đường tròn 
và 
có 
. Biết rằng 
thì vị trí tương đối của hai đường tròn đó là
Hai đường tròn tiếp xúc nhau.
Hai đường tròn ngoài nhau.
Hai đường tròn cắt nhau.
Hai đường tròn đựng nhau.
Phần 2. Câu trắc nghiệm đúng sai
Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho biểu thức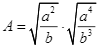 
.
a) Điều kiện xác định của biểu thức 
là 
.
b) Giá trị của 
khi 
và 
c) Giá trị của tại 
và 
là 
d) Biểu thức 
Cho hệ phương trình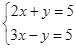 
. Biết cặp số 
là nghiệm của hệ phương trình. Tính 
Phương trình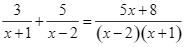 
có nghiệm 
. Tìm 
Cho hai biểu thức 
và 
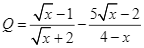với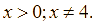 
Tính giá trị của biểu thức 
khi 
Cho hai biểu thức 
và 
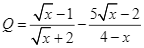với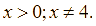 
Rút gọn biểu thức 
.
Cho hai biểu thức 
và 
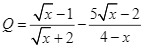với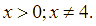 
Tìm giá trị của 
để biểu thức 
đạt giá trị nhỏ nhất.
Giải phương trình
Giải bất phương trình
Giải bài toán sau bằng cách lập hệ phương trình.
Bạn Bình mua một quyển từ điển và một món đồ chơi với tổng số tiền theo giá niêm yết là 
nghìn đồng. Vì Bình mua đúng dịp cửa hàng có chương trình khuyến mại nên khi thanh toán giá quyển từ điển được giảm giá 
, giá món đồ chơi được giảm 
. Do đó, Bình chỉ phải trả 
nghìn đồng. Hỏi Bình mua mỗi thứ giá bao nhiêu tiền?
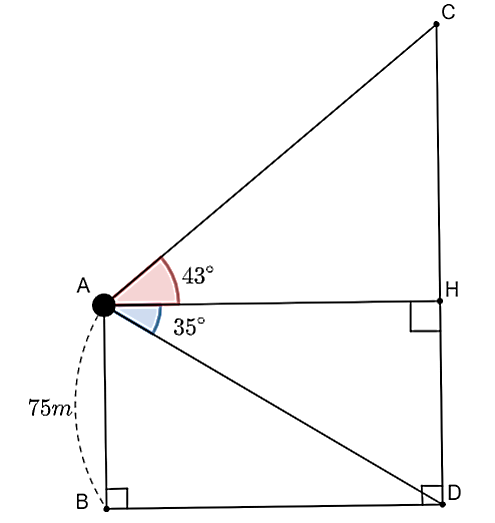
Một kĩ sư xây dựng đứng ở vị trí |
|
Cho nửa đường tròn tâm 
đường kính 
. Từ 
kẻ hai tiếp tuyến 
. Qua điểm 
thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt tiếp tuyến lần lượt ở 
và 
. Các đường thẳng 
và 
cắt nhau tại 
Chứng minh rằng 
Cho nửa đường tròn tâm 
đường kính 
. Từ 
kẻ hai tiếp tuyến 
. Qua điểm 
thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt tiếp tuyến lần lượt ở 
và 
. Các đường thẳng 
và 
cắt nhau tại 
Chứng minh rằng 
là tiếp tuyến của đường tròn đường kính 
và 
Cho nửa đường tròn tâm 
đường kính 
. Từ 
kẻ hai tiếp tuyến 
. Qua điểm 
thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt tiếp tuyến lần lượt ở 
và 
. Các đường thẳng 
và 
cắt nhau tại 
Giả sử 
. Tính diện tích hình quạt giới hạn bởi bán kính 
và cung nhỏ 
Cho nửa đường tròn tâm 
đường kính 
. Từ 
kẻ hai tiếp tuyến 
. Qua điểm 
thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt tiếp tuyến lần lượt ở 
và 
. Các đường thẳng 
và 
cắt nhau tại 
Gọi 
. Hỏi khi 
di chuyển trên 
thì trung điểm 
của 
di chuyển trên đường nào?
