Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án - Đề 09
16 câu hỏi
Cho hai biểu thức: 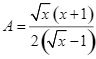 và
và 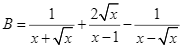 .
.
Tìm điều kiện xác định của biểu thức ![]() và
và ![]()
Cho hai biểu thức: 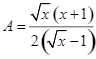 và
và 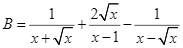 .Tính giá trị của biểu thức
.Tính giá trị của biểu thức ![]() khi
khi ![]()
Cho hai biểu thức: 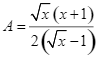 và
và 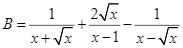 .Rút gọn biểu thức
.Rút gọn biểu thức ![]()
Cho hai biểu thức: 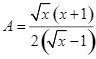 và
và 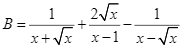 .Tìm giá trị nhỏ nhất của biểu thức
.Tìm giá trị nhỏ nhất của biểu thức ![]() với
với ![]()
Giải phương trình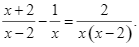
Giải bất phương trình![]()
Giải bài toán sau bằng cách lập hệ phương trình:
Một đội sản xuất dự định mỗi ngày làm ![]() sản phẩm. Khi thực hiện, mỗi ngày đội làm được
sản phẩm. Khi thực hiện, mỗi ngày đội làm được ![]() sản phẩm. Vì vậy không những hoàn thành xong trước kế hoạch 2 ngày mà còn làm thêm được
sản phẩm. Vì vậy không những hoàn thành xong trước kế hoạch 2 ngày mà còn làm thêm được ![]() sản phẩm. Tính số sản phẩm mà đội phải làm theo kế hoạch.
sản phẩm. Tính số sản phẩm mà đội phải làm theo kế hoạch.
Để lập đội tuyển năng khiếu môn bóng rổ của trường, thầy thể dục đưa ra quy định tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 15 quả bóng vào rổ, quả bóng vào rổ được cộng thêm 2 điểm; quả bóng ném ra ngoài bị trừ 1 điểm. Nếu bạn nào có số điểm từ 15 điểm trở lên thì sẽ được chọn vào đội tuyển.
Viết bất phương trình phù hợp với tình huống trên.
Để lập đội tuyển năng khiếu môn bóng rổ của trường, thầy thể dục đưa ra quy định tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 15 quả bóng vào rổ, quả bóng vào rổ được cộng thêm 2 điểm; quả bóng ném ra ngoài bị trừ 1 điểm. Nếu bạn nào có số điểm từ 15 điểm trở lên thì sẽ được chọn vào đội tuyển.Hỏi một bạn học sinh muốn được chọn vào đội tuyển thì phải ném ít nhất bao nhiêu quả bóng vào rổ?
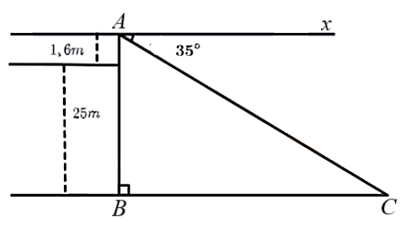
Một người có tầm mắt cao ![]() đứng trên sân thượng của một tòa nhà cao
đứng trên sân thượng của một tòa nhà cao ![]() nhìn thấy một chiếc xe đang đứng yên với góc nghiêng xuống
nhìn thấy một chiếc xe đang đứng yên với góc nghiêng xuống ![]() (như hình vẽ).Viết tỉ số lượng giác
(như hình vẽ).Viết tỉ số lượng giác ![]() của góc
của góc ![]() theo các cạnh
theo các cạnh ![]()
Một người có tầm mắt cao ![]() đứng trên sân thượng của một tòa nhà cao
đứng trên sân thượng của một tòa nhà cao ![]() nhìn thấy một chiếc xe đang đứng yên với góc nghiêng xuống
nhìn thấy một chiếc xe đang đứng yên với góc nghiêng xuống ![]() (như hình vẽ).Tính các khoảng cách từ chiếc xe đến mắt người quan sát và đến chân tòa nhà (kết quả làm tròn đến hàng đơn vị).
(như hình vẽ).Tính các khoảng cách từ chiếc xe đến mắt người quan sát và đến chân tòa nhà (kết quả làm tròn đến hàng đơn vị).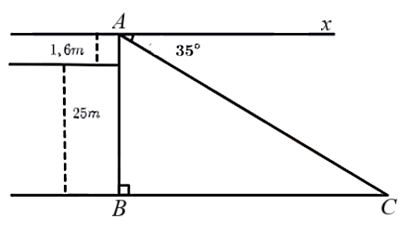
Cho ![]() vuông tại
vuông tại ![]() . Hạ
. Hạ ![]() , vẽ đường tròn tâm
, vẽ đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() và đường tròn tâm
và đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() Xác định vị trí tương đối của hai đường tròn
Xác định vị trí tương đối của hai đường tròn ![]() và
và ![]() .
.
Cho ![]() vuông tại
vuông tại ![]() . Hạ
. Hạ ![]() , vẽ đường tròn tâm
, vẽ đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() và đường tròn tâm
và đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() Chứng minh rằng
Chứng minh rằng ![]()
Cho ![]() vuông tại
vuông tại ![]() . Hạ
. Hạ ![]() , vẽ đường tròn tâm
, vẽ đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() và đường tròn tâm
và đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() Chứng minh rằng
Chứng minh rằng ![]() là tiếp tuyến của
là tiếp tuyến của ![]() .
.
Vẽ đường tròn ![]() đường kính
đường kính ![]() cắt đường thẳng
cắt đường thẳng ![]() tại
tại ![]() và
và ![]() .Cho
.Cho ![]() vuông tại
vuông tại ![]() . Hạ
. Hạ ![]() , vẽ đường tròn tâm
, vẽ đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() và đường tròn tâm
và đường tròn tâm ![]() đường kính
đường kính ![]() cắt
cắt ![]() tại
tại ![]() Chứng minh tam giác
Chứng minh tam giác ![]() cân và xác định vị trí của
cân và xác định vị trí của ![]() để chu vi tứ giác
để chu vi tứ giác ![]() lớn nhất.
lớn nhất.
Một sợi dây thép ![]() có chiều dài
có chiều dài ![]() được chia thành hai phần
được chia thành hai phần ![]() (như hình vẽ minh họa dưới đây).
(như hình vẽ minh họa dưới đây).
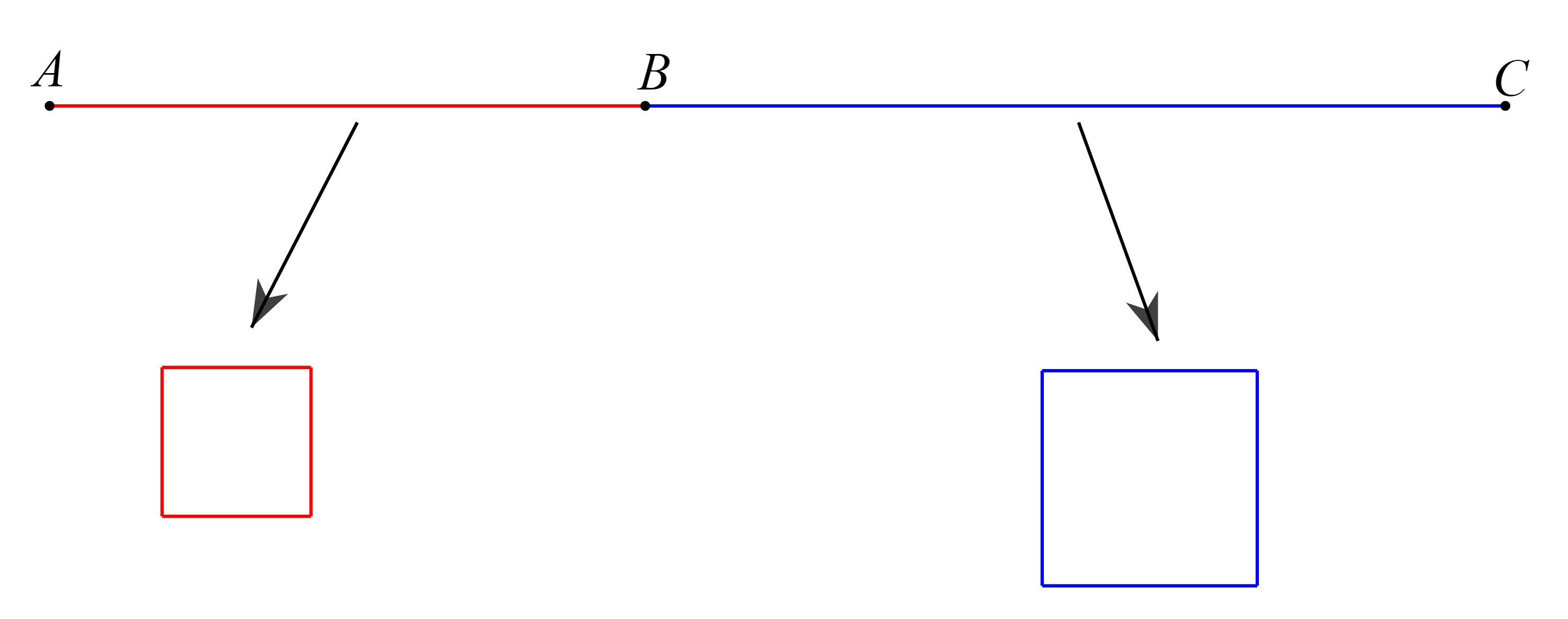
Mỗi phần đều được uốn thành một hình vuông. Hỏi phải chia sợi dây ban đầu như thế nào để tổng diện tích hai hình vuông thu được sau khi uốn là nhỏ nhất?








