Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án - Đề 08
18 câu hỏi
A. TRẮC NGHIỆM (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
![]()
![]()
![]()
![]()
Cho ![]() bất kỳ. Kết quả so sánh nào sau đây là đúng?
bất kỳ. Kết quả so sánh nào sau đây là đúng?
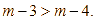
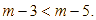
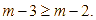
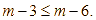
Cho tam giác ![]() vuông tại
vuông tại ![]() . Khi đó:
. Khi đó:
![]()
![]()
![]()
![]()
Góc ở tâm là góc
có đỉnh nằm trên đường tròn.
có đỉnh nằm trên bán kính của đường tròn.
có hai cạnh là hai đường kính của đường tròn.
có đỉnh trùng với tâm đường tròn.
Phần 2. Câu trắc nghiệm đúng sai
Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho biểu thức ![]() .
.
a) Điều kiện xác định của biểu thức ![]() là
là ![]() và
và ![]() .
.
b) Biểu thức ![]()
c) Với ![]() và
và ![]() thì giá trị của biểu thức
thì giá trị của biểu thức ![]() bằng
bằng ![]()
d) Khi ![]() thì
thì ![]() hoặc
hoặc ![]()
Cho bất phương trình ![]() . Biết nghiệm nhỏ nhất của bất phương trình có dạng
. Biết nghiệm nhỏ nhất của bất phương trình có dạng ![]() (với
(với ![]() là phân số tối giản có mẫu số dương). Tính giá trị biểu thức
là phân số tối giản có mẫu số dương). Tính giá trị biểu thức ![]()
Cho hình vành khuyên giới hạn bởi hai đường tròn ![]() và
và ![]() . Hỏi diện tích hình vành khuyên đó là bao nhiêu
. Hỏi diện tích hình vành khuyên đó là bao nhiêu ![]() (lấy
(lấy ![]() kết quả làm tròn đến hàng phần mười)?
kết quả làm tròn đến hàng phần mười)?
B. TỰ LUẬN (7,0 điểm)
Cho hai biểu thức: 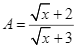 và
và 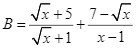 với
với ![]()
Tính giá trị của ![]() khi
khi ![]() .
.
Cho hai biểu thức: 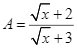 và
và 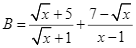 với
với ![]() Rút gọn biểu thức
Rút gọn biểu thức ![]()
Cho hai biểu thức: 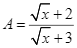 và
và 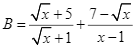 với
với ![]() Tìm giá trị của
Tìm giá trị của ![]() để biểu thức
để biểu thức ![]() nhận giá trị nguyên.
nhận giá trị nguyên.
Giải phương trình sau: ![]()
Có hai loại quặng chứa ![]() sắt và
sắt và ![]() sắt. Tính khối lượng của mỗi loại quặng đem trộn để được
sắt. Tính khối lượng của mỗi loại quặng đem trộn để được ![]() tấn quặng chứa
tấn quặng chứa ![]() sắt.
sắt.
Giải bài toán sau bằng cách lập bất phương trình:
Người ta dùng một loại xe tải để chở bia cho một nhà máy. Mỗi thùng bia 24 lon nặng trung bình ![]() Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là
Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là ![]() tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác tài xế nặng
tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác tài xế nặng ![]()
Trên nóc của một tòa nhà có một cột ăng – ten cao ![]() . Từ vị trí quan sát
. Từ vị trí quan sát ![]() cao
cao ![]() so với mặt đất, có thể nhìn thấy đỉnh
so với mặt đất, có thể nhìn thấy đỉnh ![]() và đỉnh
và đỉnh ![]() của một cột ăng – ten dưới góc
của một cột ăng – ten dưới góc ![]() và
và ![]() so với phương nằm ngang. Tính chiều cao của tòa nhà.
so với phương nằm ngang. Tính chiều cao của tòa nhà.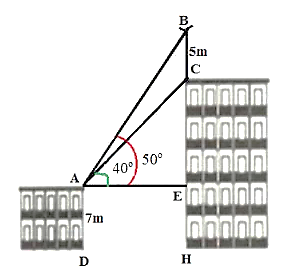
Cho đường tròn ![]() và điểm
và điểm ![]() nằm bên ngoài đường tròn. Từ
nằm bên ngoài đường tròn. Từ ![]() kẻ hai tiếp tuyến
kẻ hai tiếp tuyến ![]() với đường tròn
với đường tròn ![]() . Một đường thẳng
. Một đường thẳng ![]() đi qua
đi qua ![]() cắt đường tròn
cắt đường tròn ![]() tại hai điểm
tại hai điểm ![]() và
và ![]() (
(![]() ,
, ![]() không đi qua tâm
không đi qua tâm ![]() ). Gọi
). Gọi ![]() là trung điểm của
là trung điểm của ![]() . Đường thẳng
. Đường thẳng ![]() cắt đường tròn
cắt đường tròn ![]() tại điểm thứ hai là
tại điểm thứ hai là ![]() .Chứng minh bốn điểm
.Chứng minh bốn điểm ![]() cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
Cho đường tròn ![]() và điểm
và điểm ![]() nằm bên ngoài đường tròn. Từ
nằm bên ngoài đường tròn. Từ ![]() kẻ hai tiếp tuyến
kẻ hai tiếp tuyến ![]() với đường tròn
với đường tròn ![]() . Một đường thẳng
. Một đường thẳng ![]() đi qua
đi qua ![]() cắt đường tròn
cắt đường tròn ![]() tại hai điểm
tại hai điểm ![]() và
và ![]() (
(![]() ,
, ![]() không đi qua tâm
không đi qua tâm ![]() ). Gọi
). Gọi ![]() là trung điểm của
là trung điểm của ![]() . Đường thẳng
. Đường thẳng ![]() cắt đường tròn
cắt đường tròn ![]() tại điểm thứ hai là
tại điểm thứ hai là ![]() .Chứng minh
.Chứng minh ![]() và
và ![]() .
.
Cho đường tròn ![]() và điểm
và điểm ![]() nằm bên ngoài đường tròn. Từ
nằm bên ngoài đường tròn. Từ ![]() kẻ hai tiếp tuyến
kẻ hai tiếp tuyến ![]() với đường tròn
với đường tròn ![]() . Một đường thẳng
. Một đường thẳng ![]() đi qua
đi qua ![]() cắt đường tròn
cắt đường tròn ![]() tại hai điểm
tại hai điểm ![]() và
và ![]() (
(![]() ,
, ![]() không đi qua tâm
không đi qua tâm ![]() ). Gọi
). Gọi ![]() là trung điểm của
là trung điểm của ![]() . Đường thẳng
. Đường thẳng ![]() cắt đường tròn
cắt đường tròn ![]() tại điểm thứ hai là
tại điểm thứ hai là ![]() .Hai tiếp tuyến của đường tròn
.Hai tiếp tuyến của đường tròn ![]() tại
tại ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() . Chứng minh
. Chứng minh ![]() thuộc một đường tròn cố định khi
thuộc một đường tròn cố định khi ![]() thay đổi.
thay đổi.
Xưa kia có một vị tể tướng nổi tiếng thông thái. Đến khi tể tướng muốn cáo quan về quê, nhà vua liền ban thưởng bằng cách đưa cho tể tướng một đoạn dây dài ![]() mét và nói: “Ngươi hãy căng sợi dây này thành một hình chữ nhật, sao cho hai đầu dây chạm vào nhau. Khi đó, mảnh đất hình chữ nhật sẽ thuộc về ngươi”. Hỏi tể tướng sẽ căng sợi dây như thế nào để mảnh đất có diện tích lớn nhất?
mét và nói: “Ngươi hãy căng sợi dây này thành một hình chữ nhật, sao cho hai đầu dây chạm vào nhau. Khi đó, mảnh đất hình chữ nhật sẽ thuộc về ngươi”. Hỏi tể tướng sẽ căng sợi dây như thế nào để mảnh đất có diện tích lớn nhất?








