Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án (Đề 8)
22 câu hỏi
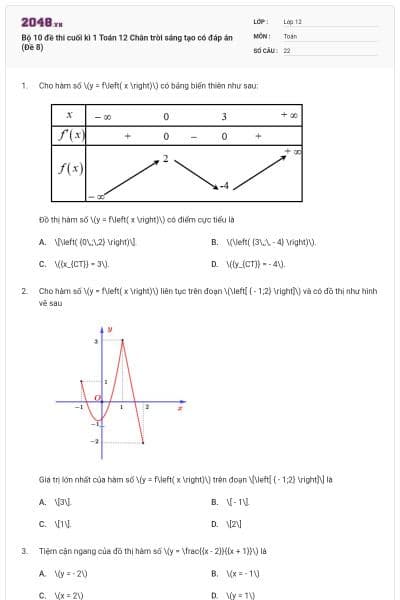
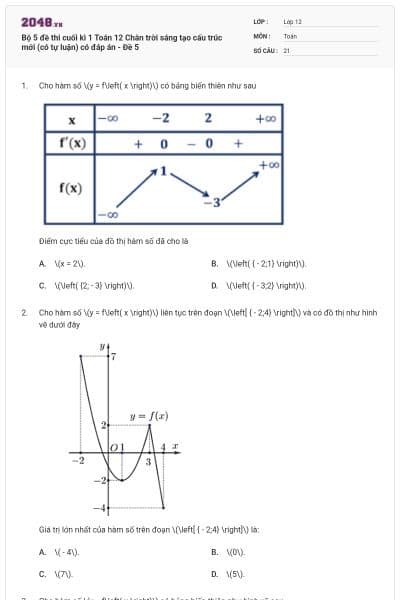
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
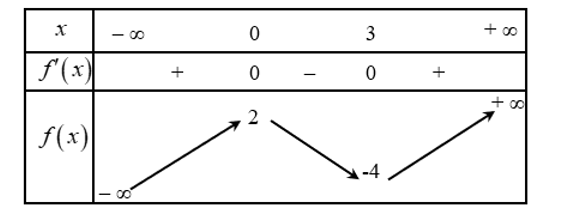
Đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là
\[\left( {0\,;\,2} \right)\].
\(\left( {3\,;\, - 4} \right)\).
\({x_{CT}} = 3\).
\({y_{CT}} = - 4\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ sau
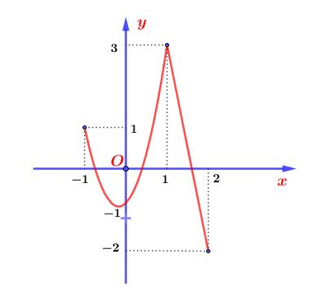
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \[\left[ { - 1;2} \right]\] là
\[3\].
\[ - 1\].
\[1\].
\[2\]
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x - 2}}{{x + 1}}\) là
\(y = - 2\)
\(x = - 1\)
\(x = 2\)
\(y = 1\)
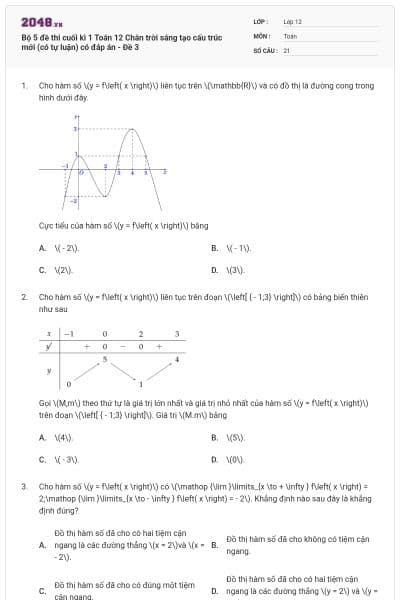
Đường cong ở hình bên dưới là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\)với \[a\],\[b\],\[c\],\[d\] là các số thực.
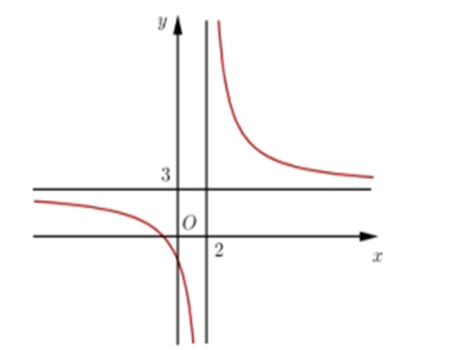
Mệnh đề nào dưới đây đúng?
\(y' > 0\),\(\forall x \ne 2\).
\(y' > 0\),\(\forall x \ne 3\).
\(y' < 0\),\(\forall x \ne 2\).
\(y' < 0\),\(\forall x \ne 3\).
Cho hàm số \(y = \frac{{{x^2} - 2x + 5}}{{x - 1}}\). Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right) \cup \left( {1\,;\,3} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 1;\,3} \right){\rm{\backslash }}\left\{ 1 \right\}\).
Hàm số nghịch biến trên mỗi khoảng \(\left( { - 1;\,1} \right)\)và \(\left( {1\,;\,3} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
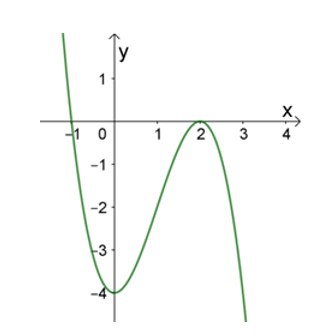
\(y = \frac{{x - 1}}{x}\).
\(y = {x^3} + 3{x^2} - 4\).
\(y = - {x^3} + 3x - 4\).
\(y = - {x^3} + 3{x^2} - 4\).
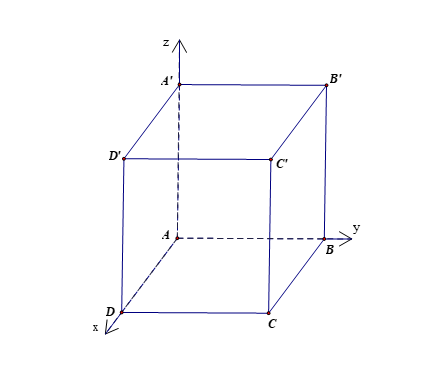
Trong không gian, cho hình hộp \(ABCD\,A'B'C'D'\). Vectơ đối của vectơ \[\overrightarrow {AA'} \]là
\[\overrightarrow {A'C'} \].
\[\overrightarrow {BA'} \].
\[\overrightarrow {BB'} \].
\[\overrightarrow {C'C} \].
Trong không gian \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\). Biết \(A\left( {1;0;1} \right)\), \(C'\left( {4;5; - 5} \right)\). Tìm tọa độ tâm \(I\) của hình hộp.
\(I\left( {5;5; - 2} \right)\).
\(I\left( { - \frac{5}{2};\frac{5}{2}; - 2} \right)\).
\(I\left( {\frac{5}{2};\frac{5}{2};2} \right)\).
\(I\left( {\frac{5}{2};\frac{5}{2}; - 2} \right)\).
Cho tứ diện \(S.ABC\) có đáy là tam giác đều cạnh \(a\), \(SB\) vuông góc với đáy và \(SB = \sqrt 3 a\). Góc giữa hai vectơ \(\left( {\overrightarrow {AB} ,\overrightarrow {AS} } \right)\) là

\[60^\circ \].
\[30^\circ \].
\[45^\circ \].
\[90^\circ \].
Trong không gian tọa độ \(Oxyz\), cho điểm \(A\left( {1;0; - 2} \right)\), \(B\left( {1; - 1;0} \right)\). Tìm toạ độ điểm \(C\)nằm trên trục \(Oz\) sao cho \(AB \bot BC\)?
\(\left( {0;0;1} \right)\).
\(\left( {0;0; - 1} \right)\).
\(\left( {0;0;\frac{1}{2}} \right)\).
\(\left( {0;0; - \frac{1}{2}} \right)\).
Thống kê chỉ số chất lượng không khí (AQI) tại một địa điểm vào các ngày trong tháng 6/2022 được cho trong bảng sau
Chỉ số AQI | \(\left[ {0;50} \right)\) | \(\left[ {50;100} \right)\) | \(\left[ {100;150} \right)\) | \(\left[ {150;200} \right)\) | \(\left[ {200;250} \right)\) |
Số ngày | 5 | 11 | 7 | 4 | 3 |
Khoảng biến thiên \(R\) của mẫu số liệu ghép nhóm trên là.
\(R = 50\).
\(R = 250\).
\(R = 150\).
\(R = 8\).
Khẳng định nào sau đây sai?
Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là căn bậc hai số học của phương sai.
Phương sai càng lớn thì mẫu số liệu càng phân tán.
Phương sai của mẫu số liệu ghép nhóm là căn bậc hai số học của độ lệch chuẩn.
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có bảng biến thiên như hình vẽ dưới đây. Xét tính đúng sai của các khẳng định sau:
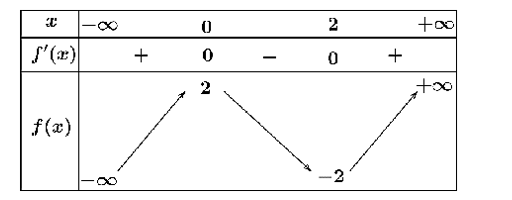
a) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
b) Hàm số \(g\left( x \right) = 2x - 3f\left( x \right)\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
c) \(f\left( {{{\sin }^2}x} \right) < f\left( {\frac{3}{2}} \right)\).
d) Hàm số \(y = f\left( {2 - 3x} \right)\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
Cho hàm số \(y = \frac{{x - {m^2} - 2}}{{x - m}}\) (với tham số \(m\)). Xét tính đúng sai của các khẳng định sau:
a) Khi \(m = 1\) hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
b) Khi \(m = 1\) thì trên đoạn \(\left[ {1;4} \right]\) hàm số đạt giá trị lớn nhất bằng \(\frac{1}{2}\).
c) \(y = 1\) là tiệm cận ngang của đồ thị hàm số.
d) Có 1 giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(y = \frac{{x - {m^2} - 2}}{{x - m}}\) trên đoạn \(\left[ {0;4} \right]\) bằng \( - 1\).
Trong không gian \(Oxyz\), cho hai điểm \(M\left( {2;3; - 1} \right),N\left( { - 1;1;1} \right)\).
a) Hình chiếu của điểm \(M\) trên trục \(Oy\) có tọa độ là \(\left( { - 2;3;1} \right)\).
b) Gọi \(E\) là điểm đối xứng của điểm \(M\) qua \(N\). Tọa độ của điểm \(E\) là \(\left( { - 4; - 1;3} \right)\).
c) Cho \(P\left( {1;m - 1;3} \right)\). Tam giác \(MNP\) vuông tại N khi và chỉ khi \(m = 1\).
d) Điểm \(I\left( {a;b;c} \right)\) nằm trên mặt phẳng \(\left( {Oxy} \right)\) thỏa mãn \(T = \left| {3\overrightarrow {IM} - \overrightarrow {IN} } \right|\) đạt giá trị nhỏ nhất. Khi đó \(2a + b + c = 9\).
Anh Bình đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh Bình thống kê số tiền thu được mỗi tháng trong vòng 40 tháng theo mỗi lĩnh vực cho kết quả như sau:
Số tiền (triệu đồng) | \[\left[ {15;20} \right)\] | \[\left[ {20;25} \right)\] | \[\left[ {25;30} \right)\] | \[\left[ {30;35} \right)\] | \[\left[ {35;40} \right)\] |
Số tháng đầu tư vào lĩnh vực A | 5 | 10 | 8 | 8 | 9 |
Số thángđầu tư vào lĩnh vực B | 6 | 8 | 9 | 8 | 9 |
a) Khoảng biến thiên về số tháng đầu từ vào lĩnh vực A và B ở mẫu số liệu trên bằng nhau.
b) Số tiền trung bình đầu tư vào lĩnh vực A lớn hơn số tiền trung bình đầu tư vào lĩnh vực B.
c) Phương sai của số tiền thu được khi đầu tư vào lĩnh vực A là \[46,9375\].
d) Anh Bình đầu tư vào lĩnh vực A rủi ro hơn đầu tư vào lĩnh vực B.
Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{1}{2}x - \sqrt {x + 1} \) trên đoạn \(\left[ {0;3} \right]\). Tổng \(S = 2M - m\) bằng bao nhiêu?
Chi phí để loại \(x\left( \% \right)\) chất gây ô nhiễm là \(C\) (nghìn đô) với \(C\left( x \right) = \frac{{12x}}{{100 - x}}\). Chi phí để loại bỏ \(50\% \) chất gây ô nhiễm là bao nhiêu nghìn đô?
Một con cá hồi bơi ngược dòng để vượt khoảng cách là \(100\;{\rm{km}}\). Vận tốc dòng nước là \(5\;\left( {{\rm{km/h}}} \right)\). Nếu vận tốc bơi của cá khi nước đứng yên là \(v\;\left( {{\rm{km/h}}} \right)\), \(\left( {v > 5} \right)\) thì năng lượng tiêu hao của cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c \cdot {v^3} \cdot t\), trong đó \(c\) là hằng số dương, \(E\) được tính bằng Jun. Biết rằng vận tốc bơi của cá khi nước đứng yên thuộc khoảng \(\left( {a;b} \right)\) thì năng lượng tiêu hao của cá giảm. Hãy tính giá trị lớn nhất của \(b - a\) (kết quả làm tròn tới hàng phần mười).
Trên hệ trục tọa độ \(Oxy\), cho đồ thị hàm số \(\left( C \right):y = \frac{{{x^2} + x + 1}}{{x + 1}}\) với \(x > - 1\) mô tả chuyển động của một chiếc thuyền trên biển. Một trạm phát sóng đặt tại điểm \(I\left( { - 1; - 1} \right)\), biết hoành độ điểm \(M\)thuộc đồ thị \(\left( C \right)\) mà tại đó thuyền thu được sóng tốt nhất là \({x_0} = \frac{1}{{\sqrt[n]{a}}} - b\) (loại trừ các điều kiện ảnh hưởng đến việc thu phát sóng). Tính giá trị biểu thức \(P = a \cdot n + b\).
Theo định luật II Newton (Vật lí 10 - Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 60): Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật: \(\vec F = m\vec a\) trong đó \(\vec a\) là vectơ gia tốc \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right),\vec F\) là vectơ lực (N), \(m\left( {{\rm{\;kg}}} \right)\) là khối lượng của vật.

Muốn truyền cho quả bóng có khối lượng \(0,5{\rm{\;kg}}\)một gia tốc \(50{\rm{\;m}}/{{\rm{s}}^2}\) thì cần một lực đá có độ lớn là bao nhiêu Newton?
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 10 m, chiều rộng là 6m và chiều cao là 4 m. Một chiếc quạt được treo trên trần nhà sao cho là điểm chính giữa của phòng học.
Xét hệ trục tọa độ \(Oxyz\)có gốc (\(O \equiv A\)) trùng với một góc phòng và mặt phẳng (\(Oxy\)) trùng với mặt sàn, đơn vị đo được lấy theo mét . Gọi \[I(a;b;c)\]là tọa độ của điểm treo quạt. Tính giá trị \(a + b + c\)?