Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án (Đề 6)
22 câu hỏi
Cho hàm số có đồ thị như hình bên. Khẳng định nào sau đây là đúng?
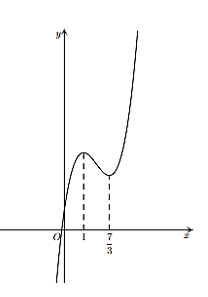
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {\frac{7}{3}; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau
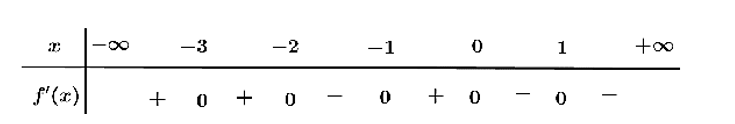
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left( { - 1; + \infty } \right)\).
\(f\left( 1 \right)\).
\(f\left( { - 2} \right)\).
\(f\left( { - 1} \right)\).
\(f\left( 0 \right)\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x + 1}}{{x - 1}}\) có phương trình
\(y = \frac{1}{3}\).
\(y = 3\).
\(y = - 1\).
\(y = 1\).
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình \(f\left( x \right) = - 1\) là
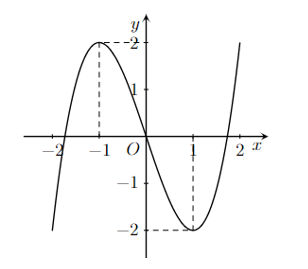
3.
1.
0.
2.
Cho hàm số \(y = \frac{{2x + 8}}{{5x - 9}}\). Hàm số nghịch biến trên khoảng nào trong các khoảng sau?
\(\left( { - \infty ;5} \right)\).
\(\left( { - \infty ; + \infty } \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( {2; + \infty } \right)\)
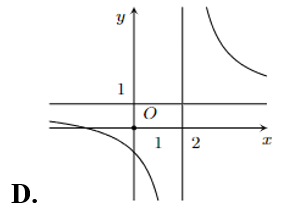
Đồ thị của hàm số \(y = \frac{{x - 2}}{{x + 1}}\) là
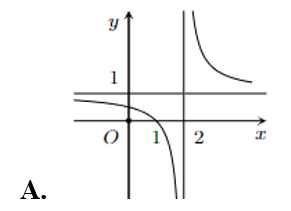
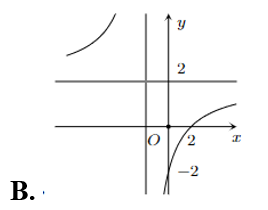
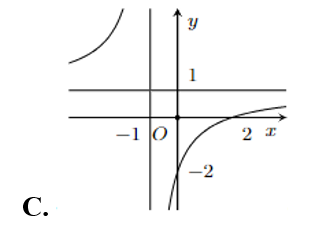
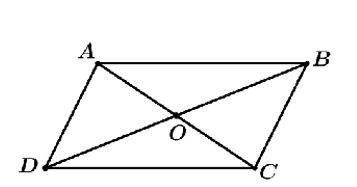
Cho \(O\) là tâm hình bình hành \(ABCD\). Hỏi vectơ \(\overrightarrow {AO} - \overrightarrow {DO} \) bằng vectơ nào?
\(\overrightarrow {BA} \).
\(\overrightarrow {AD} \).
\(\overrightarrow {DC} \).
\(\overrightarrow {AC} \).
Trong không gian \(Oxyz\), cho \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là
\(\left( {2; - 1; - 3} \right)\).
\(\left( { - 3;2; - 1} \right)\).
\(\left( {2; - 3; - 1} \right)\).
\(\left( { - 1;2; - 3} \right)\).
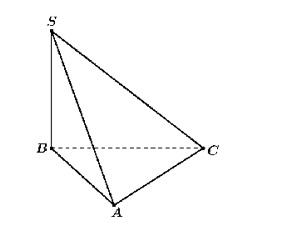
Cho tứ diện \(S.ABC\) có đáy là tam giác đều cạnh \(a\), \(SB\) vuông góc với đáy và \(SB = \sqrt 3 a\). Góc giữa hai vectơ \(\left( {\overrightarrow {AB} ,\overrightarrow {AS} } \right)\) là
\(60^\circ \).
\(30^\circ \).
\(45^\circ \).
\(90^\circ \).
Cho tam giác \(ABC\) biết \(A\left( {2; - 1;3} \right)\) và trọng tâm của tam giác có tọa độ là \(G\left( {2;1;0} \right)\). Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} \) có tọa độ là
\(\left( {0; - 9;9} \right)\).
\(\left( {0;6;9} \right)\).
\(\left( {0;9; - 9} \right)\).
\(\left( {0;6; - 9} \right)\).
Bảng thống kê cân nặng 50 quả thanh long được lựa chọn ngẫu nhiên sau khi thu hoạch ở nông trường:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là (làm tròn kết quả đến hàng phần mười)
63,5.
65,3.
382,7.
319,2.
Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng 3 thì có phương sai bằng
\({s^2} = \sqrt 3 \).
\({s^2} = 3\).
\({s^2} = 9\).
\({s^2} = 6\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y = f'\left( x \right)\)là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.
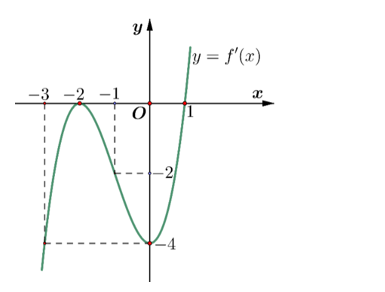
Xét tính đúng hoặc sai của các mệnh đề sau:
a) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
b) Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
c) \(f'\left( 2 \right) = 4\).
d) Hàm số \(g\left( x \right) = f\left( x \right) - \frac{1}{2}{x^2} + x + 2024\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} + 4x - 1}}{{x - 1}}\) có đồ thị là \(\left( C \right)\). Xét tính đúng sai của các khẳng định sau:
a) Số khoảng đồng biến và nghịch biến của hàm số là bằng nhau.
b) Đồ thị hàm số \(f\left( x \right)\) đạt cực đại tại điểm có tọa độ \(\left( { - 1;2} \right)\).
c) Đường thẳng \(x = 1\) là đường tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\).
d) Trên đồ thị \(\left( C \right)\) tồn tại đúng 4 điểm có tọa độ nguyên.
Trong không gian \[Oxyz\], cho \(\Delta ABC\)với \(A\left( {1\,;\,2\,;\,3} \right)\), \(B\left( {4\,;\,5\,;\,6} \right)\), \(C\left( {2\,;\,7\,;\,4} \right)\)
a) Tọa độ vectơ \(\overrightarrow {AB} = \left( {3;3;3} \right)\).
b) Tọa độ trọng tâm \(G\) của \(\Delta ABC\) là \(G\left( {\frac{7}{3};\,\frac{{14}}{3}\,;\,\frac{{13}}{3}} \right)\).
c) Tích vô hướng của hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là 31.
d) Chu vi và diện tích của \(\Delta ABC\) lần lượt là \(8\sqrt 3 \) và \(6\sqrt 2 \,\).
Bảng sau thống kê lại tổng số giờ nắng trong tháng 6 của các năm từ 2002 đến 2021 tại hai trạm quan trắc đặt ở Nha Trang và Quy Nhơn.
Số giờ nắng | \([130;160)\) | \([160;190)\) | \([190;220)\) | \([220;250)\) | \([250;280)\) | \([280;310)\) |
Số năm ở Nha Trang | 1 | 1 | 1 | 8 | 7 | 2 |
Số năm ở Quy Nhơn | 0 | 1 | 2 | 4 | 10 | 3 |
(Nguồn: Tổng cục Thống kê)
Các mệnh đề sau đúng hay sai?
a) Khoảng biến thiên của mẫu số liệu của Quy Nhơn là 180.
b) Xét số liệu của Nha trang ta có phương sai của mẫu số liệu ghép nhóm là: 1248,75.
c) Xét số liệu của Quy Nhơn ta có độ lệch chuẩn của mẫu số liệu ghép nhóm (làm tròn kết quả đến hàng phần trăm) là: \(30,59\).
d) Nếu so sánh theo độ lệch chuẩn thì số giờ nắng trong tháng 6 của Nha Trang đồng đều hơn.
Biết hàm số \(y = {x^3} - 3{x^2} - 9x + 28\) đạt giá trị nhỏ nhất trên đoạn \(\left[ {0;4} \right]\) tại \({x_0}\). Tính \(P = {x_0} + 2\).
Cho hàm số \(y = \frac{{2x + m}}{{mx - 1}}\). Có bao nhiêu giá trị của \(m\)để đồ thị hàm số có tiệm cận đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 2.
Cho một tấm nhôm hình chữ nhật có kích thước \[15\,{\rm{cm}} \times 24\,{\rm{cm}}\]. Người ta cắt bỏ 4 góc của tấm tôn 4 miếng hình vuông bằng nhau rồi gò lại thành một hình hộp chữ nhật không có nắp. Để thể tích của hình hộp đó lớn nhất thì độ dài cạnh hình vuông của các miếng tôn bị cắt bỏ bằng bao nhiêu?
Một doanh nghiệp sản xuất độc quyền một loại sản phẩm. Giả sử khi sản xuất và bán hết \(x\) sản phẩm đó \(\left( {0 < x \le 2000} \right)\), tổng số tiền doanh nghiệp thu được (đơn vị: chục nghìn đồng) là \(f\left( x \right) = 2000x - {x^2}\) và tổng chi phí (đơn vị: chục nghìn đồng) doanh nghiệp chi ra là \(g\left( x \right) = {x^2} + 1440x + 50\). Giả sử mức thuế phụ thu trên một đơn vị sản phẩm bán được là \(t\) (chục nghìn đồng) \(\left( {0 < t < 300} \right)\). Mức thuế phụ thu \(t\) (trên một đơn vị sản phẩm) sao cho nhà nước nhận được số tiền thuế phụ thu lớn nhất và doanh nghiệp cũng thu được lợi nhuận lớn nhất theo mức thuế phụ thu đó là bao nhiêu đồng?
Cho tứ diện \(ABCD\). Trên các cạnh \(AD\) và \(BC\) lần lượt lấy \(M,N\) sao cho \(AM = 3MD\), \(BN = 3NC\). Gọi \(P,Q\) lần lượt là trung điểm của \(AD\) và \(BC\). Phân tích vectơ \(\overrightarrow {MN} \) theo hai vectơ \(\overrightarrow {PQ} \) và \(\overrightarrow {DC} \) ta được \(\overrightarrow {MN} = a\overrightarrow {PQ} + b\overrightarrow {DC} \). Tính \(a + 2b\).
Trong không gian Oxyz, cho hai điểm \(A\left( {1;2;1} \right);B\left( {2; - 1;3} \right)\) và điểm \(M\left( {a;b;0} \right)\) sao cho \(M{A^2} + M{B^2}\) nhỏ nhất. Tính \(a + b\).