Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án (Đề 5)
22 câu hỏi
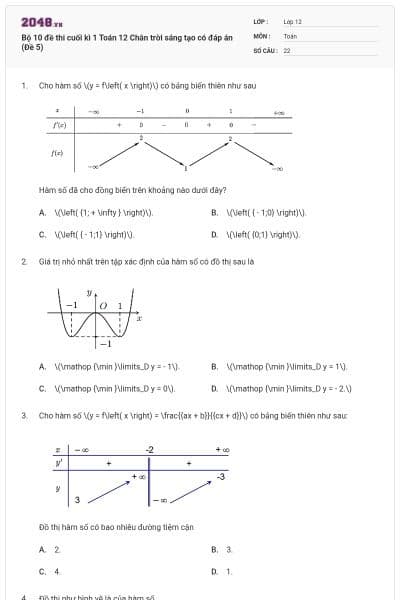
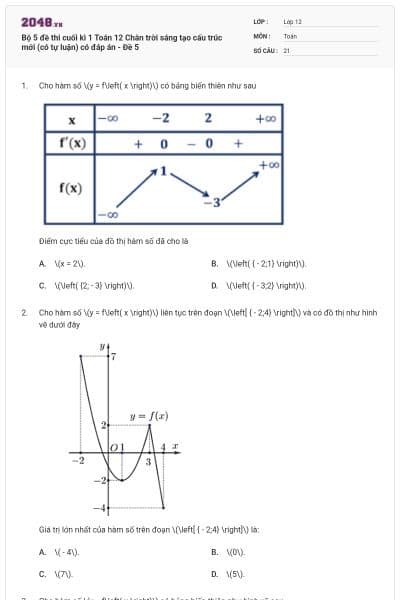
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
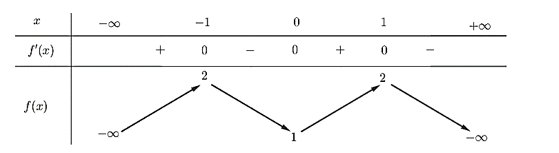
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( {1; + \infty } \right)\).
\(\left( { - 1;0} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\).
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là
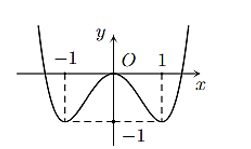
\(\mathop {\min }\limits_D y = - 1\).
\(\mathop {\min }\limits_D y = 1\).
\(\mathop {\min }\limits_D y = 0\).
\(\mathop {\min }\limits_D y = - 2.\)
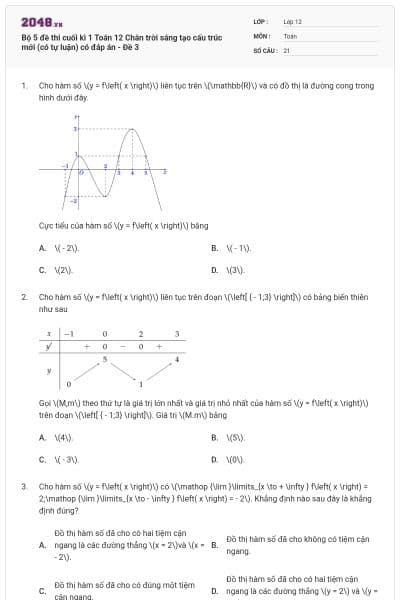
Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) có bảng biến thiên như sau:
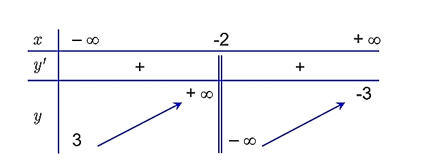
Đồ thị hàm số có bao nhiêu đường tiệm cận
2.
3.
4.
1.
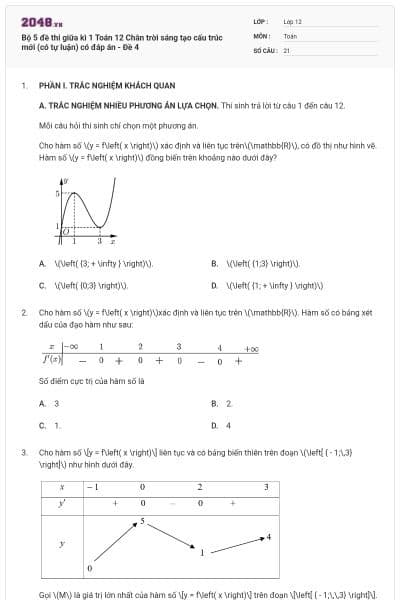
Đồ thị như hình vẽ là của hàm số
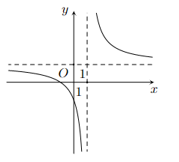
\(y = \frac{{x - 1}}{{ - x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{ - x + 1}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
Hàm số \(y = {x^4} - 2{x^2} + 1\) nghịch biến trên các khoảng nào sau đây?
\(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( {0; + \infty } \right)\).
\(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right)\).
\(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nào sau đây có một đường tiệm cận?
\(y = \frac{{x + 3}}{{2x - 1}}\).
\(y = \frac{{{x^2} + 3x - 2}}{{x + 3}}\).
\(y = \frac{{2x}}{{{x^2} + 1}}\).
\(y = \frac{4}{{x - 1}}\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Khi đó, vectơ bằng vectơ \(\overrightarrow {AB} \) là vectơ nào dưới đây?
\(\overrightarrow {D'C'} \).
\(\overrightarrow {BA} \).
\(\overrightarrow {CD} \).
\(\overrightarrow {B'A'} \).
Trong không gian \(Oxyz\), cho điểm \(M\left( {1; - 2;3} \right)\). Chọn khẳng định đúng trong các khẳng định sau.
\(\overrightarrow {OM} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \).
\(\overrightarrow {MO} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \).
\(\overrightarrow {OM} = \overrightarrow k - 2\overrightarrow j + 3\overrightarrow i \).
\(\overrightarrow {OM} = \overrightarrow j - 2\overrightarrow i + 3\overrightarrow k \).
Gọi \(G\) là trọng tâm của tứ diện \(ABCD\). Trong các khẳng định sau, khẳng định nào sai?
\(\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
\(\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\).
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow u = \left( {1;0; - 1} \right)\) và \(\overrightarrow v = \left( {2;1; - 2} \right)\). Tích vô hướng \(\overrightarrow u .\overrightarrow v \) bằng
0.
1.
4.
2.
Cho mẫu số liệu ghép nhóm cho bởi bảng như hình sau

Khoảng biến thiên của mẫu số liệu là
3.
9.
8.
15.
Cho mẫu số liệu ghép nhóm sau

Gọi \(\overline x \) là số trung bình cộng của mẫu số liệu trên.
\({s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_m}{{\left( {{x_m} - \overline x } \right)}^2}}}{n}\).
Công thức trên dùng để tính
Phương sai.
Độ lệch chuẩn.
Giá trị trung bình.
Độ phân tá
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các khẳng định sau
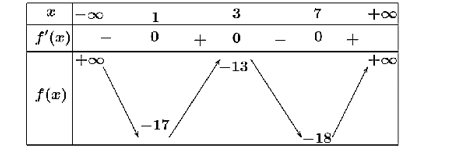
a) Hàm số nghịch biến trên khoảng \(\left( {1;7} \right)\).
b) Hàm số đạt giá trị nhỏ nhất tại \(x = 7\).
c) \(f\left( 1 \right) < f\left( 3 \right)\).
d) Tổng giá trị lớn nhất và giá trị nhỏ nhất là −31.
Cho hàm số \(y = {x^3} - 3x + 1\). Xét tính đúng hoặc sai của các mệnh đề sau:
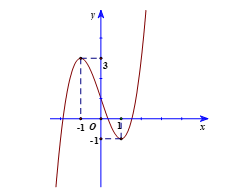
a) Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right)\).
b) Trên khoảng \(\left( { - \infty ;1} \right)\), hàm số có giá trị nhỏ nhất.
c) Hàm số có đồ thị như hình
d) Gọi \(A,B\)lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số. Khi đó, diện tích tam giác \(ABC\)là \(12\) với \(C( - 1;2)\).
Trong không gian với hệ tọa độ \(Oxyz,\)cho hình bình hành \(ABCD\) có \(A\left( { - 3;4;2} \right)\),\(B\left( { - 5;6;2} \right)\), \(C\left( { - 10;17; - 7} \right)\).
a) Tọa độ trung điểm của \(AB\) là \(I\left( { - 4;5;2} \right)\).
b) Tọa độ vectơ \(\overrightarrow {AB} = \left( {2; - 2;0} \right)\).
c) \(\overrightarrow {AB} .\overrightarrow {AD} = 10\).
d) Tọa độ chân đường cao vẽ từ \(A\) của tam giác \(ABD\) là \(H\left( { - \frac{{86}}{{19}};\frac{{87}}{{19}};\frac{{65}}{{19}}} \right)\).
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B được cho dưới bảng sau.

Xét tính đúng, sai của các mệnh đề sau
a) Khoảng biến thiên của mẫu số liệu nhà đầu tư vào lĩnh vực A là 25.
b) Độ lệch chuẩn của mẫu số liệu số nhà đầu tư vào lĩnh vực A là 5,83 (làm tròn đến hàng phần trăm).
c) Độ lệch chuẩn của mẫu số liệu số nhà đầu tư vào lĩnh vực B là 7,01 (làm tròn đến hàng phần trăm).
d) Nếu so sánh theo độ lệch chuẩn thì tiền lãi của các nhà đầu tư trong lĩnh vực A có xu hướng phân tán rộng hơn so với tiền lãi của các nhà đầu tư trong lĩnh vực B.
Một vật chuyển động theo quy luật \(s = - \frac{1}{3}{t^3} + 6{t^2}\) với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu m/s?
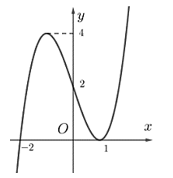
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Xác định số tiệm cận của đồ thị hàm số \(y = \frac{{{x^2} - 1}}{{{f^2}\left( x \right) - f\left( x \right)}}\).
Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200 m3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 350 nghìn đồng/m2. Hãy xác định chi phí thấp nhất để xây bể (làm tròn đến đơn vị triệu đồng).
Giả sử doanh số bán hàng (đơn vị triệu đồng) của một sản phẩm mới trong vòng 1 số năm nhất định tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = 500\left( {{t^2} + m{e^{ - t}}} \right)\), với \(t \ge 0\) là thời gian tính bằng năm kể từ khi phát hành sản phẩm mới, \(m \le 0\) là tham số. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ bán hàng. Biết rằng tốc độ bán hàng luôn tăng trong khoảng thời gian 10 năm đầu phát hành sản phẩm, khi đó giá trị nhỏ nhất của m bằng bao nhiêu?
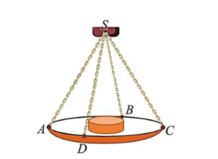
Một chiếc cân đòn tay đang cân một vật có khối lượng \(m = 3{\rm{kg}}\)được thiết kế với đĩa cân được giữ bởi bốn đoạn xích \(SA,SB,SC,SD\) sao cho \(S.ABCD\)là hình chóp đều có \(\widehat {ASC} = 90^\circ \). Biết độ lớn của lực căng cho mỗi sợi xích có dạng \(\frac{{a\sqrt 2 }}{4}\). Lấy \(g = 10{\rm{m/}}{{\rm{s}}^{\rm{2}}}\). Khi đó giá trị của a bằng bao nhiêu?
Trong không gian \(Oxyz\) cho ba điểm \(A\left( {3;2; - 1} \right)\), \(B\left( { - 1; - x;1} \right)\), \(C\left( {7; - 1;y} \right)\). Khi \(A,B,C\) thẳng hàng thì giá trị biểu thức \(x + y\) bằng bao nhiêu?