Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án (Đề 3)
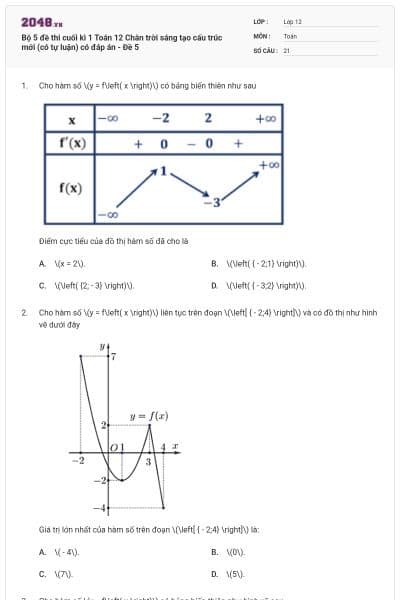
23 câu hỏi
Cho hàm số y = f(x) có đồ thị là đường cong hình bên
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
.
.
.
.
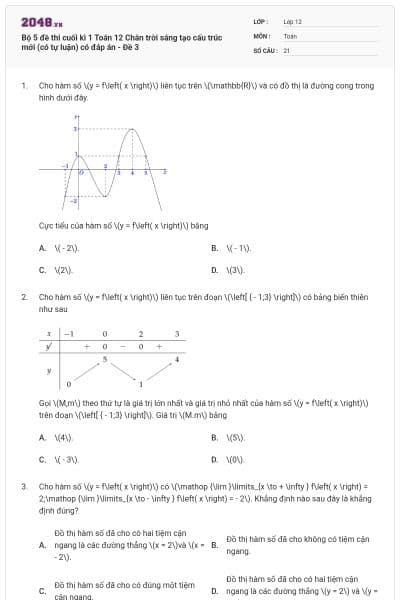
Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ sau
![Cho hàm số y = f(x) liên tục trên đoạn [-1;2] và có đồ thị như hình vẽ sau Giá trị lớn nhất của hàm số y = f(x) trên đoạn [1;2] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/12/blobid37-1733737873.png)
Giá trị lớn nhất của hàm số trên đoạn là
3.
.
1.
2
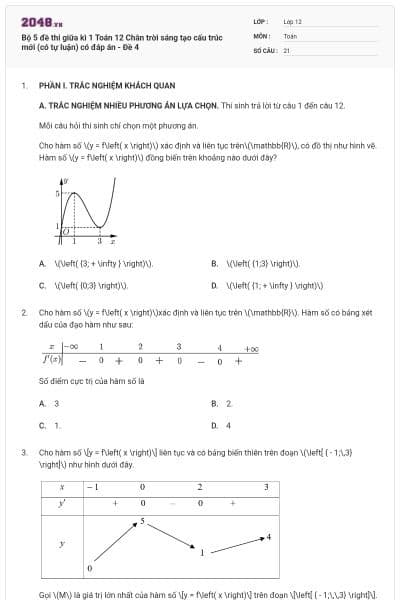
Hàm số đồng biến trên khoảng nào trong các khoảng dưới đây?
.
.
.
.
Gọi m và M lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn Mối liên hệ giữa M và m là
.
.
.
.
Cho hình hộp ABCD.A'B'C'D'. Vectơ bằng vectơ nào dưới đây?
.
.
.
Trong không gian Oxyz, biết . Toạ độ của điểm M là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm , , . Tích vô hướng của hai vectơ và là
.
.
8.
- 8.
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ và ?
.
.
.
.
Cho hàm số \(y = f(x)\) có đồ thị là đường cong hình bên
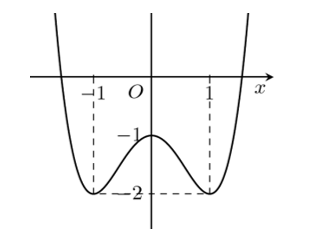
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\((1; + \infty )\).
\((0;1)\).
\(( - 1;0)\).
\(( - \infty ;0)\).
Cho hai điểm \(M\left( {0\,;\,0\,;\,2} \right)\) và \(N\left( {4\,;\, - 2;\,6} \right)\). Tìm tọa độ điểm \(P\) sao cho \(N\) là trung điểm của \(MP\)?
\(P\left( {2\,;\, - 1\,;\,4} \right)\).
\(\left( {4\,;\, - 2\,;\,4} \right)\).
\(\left( {2\,;\, - 1\,;\,2} \right)\).
\(P\left( {8\,;\, - 4\,;\,10} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow u = \left( {3; - 1;1} \right)\) và \(\overrightarrow v = \left( {1;2; - 2} \right)\). Độ dài của vectơ \(\overrightarrow u + \overrightarrow v \) là
\(\sqrt {10} \).
\(\sqrt {11} + 3\).
\(3\sqrt 2 \).
\(5\).
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được thống kê ở bảng sau:
Thời gian sử dụng | \(\left[ {7,2;7,4} \right)\) | \(\left[ {7,4;7,6} \right)\) | \(\left[ {7,6;7,8} \right)\) | \(\left[ {7,8;8,0} \right)\) |
Số máy | 2 | 4 | 7 | 6 |
Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?
\(0,192\).
\(0,197\).
\(0,037\).
\(0,2\).
Bốn bạn Ánh, Ba, Châu, Dũng cùng là thành viên của một câu lạc bộ rubik. Trong một lần luyện tập rubik với nhau, mỗi bạn đã cùng giải rubik 30 lần liên tiếp và thống kê kết quả lại ở bảng sau:
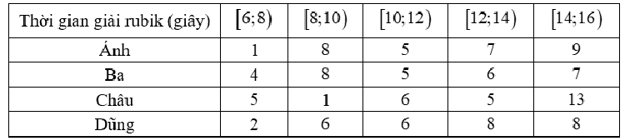
Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì bạn nào có tốc độ giải rubik đồng đều nhất?
Ánh.
Ba.
Châu.
Dũng.
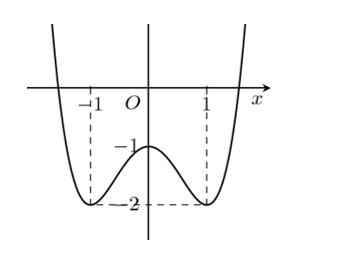
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\)có đồ thị như hình vẽ dưới đây:
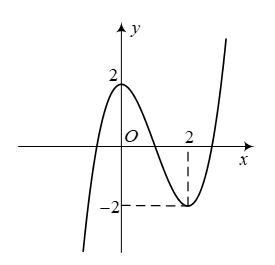
a) Hàm số đạt cực đại tại\(x = 2\).
b) Có 3 giá trị nguyên của \(m\)để phương trình \(f\left( x \right) = m\)có 3 nghiệm phân biệt .
c) Đường cong trên là đồ thị hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2\).
d) Gọi \(M\)và \(m\)lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( {2\sin x + 1} \right)\)thì \(M + m = 5\).
Cho hàm số \(y = \frac{{x - 1}}{{2x - 3}}\)\[\left( C \right)\].
a) Tiệm cận đứng của hàm số là \(x = \frac{3}{2}\).
b) Tọa độ giao điểm hai đường tiệm cận thuộc đường thẳng \(x - y - 1 = 0\)
c) Đường thẳng \(2x + y - 1 = 0\) cắt tiệm cận đứng, tiệm cận ngang của hàm số tại các điểm A và B. Diện tích của tam giác \(IAB\)bằng \(\frac{{25}}{4}\), với \(I\)là giao điểm hai đường tiệm cận.
d) Gọi \(I\) là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ \(I\) đến một tiếp tuyến bất kỳ của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng \(\frac{1}{{\sqrt 2 }}\).
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow {OA} = \left( {2; - 1;5} \right)\) và điểm \(B\left( {5; - 5;7} \right)\).
a) Tọa độ của điểm \(A\) là \(\left( {2; - 1;5} \right)\).
b) Gọi \(C\left( {a;b;c} \right)\) thỏa mãn \(\Delta ABC\) nhận \(G\left( {1;1;1} \right)\) làm trọng tâm. Khi đó \(a + b + c = - 4\).
c) Nếu \(A,B,M\left( {x;y;1} \right)\) thẳng hàng thì tổng \(x + y = 3\).
d) Cho \(N \in \left( {Oxy} \right)\) để \(\Delta ABN\) vuông tại \(A\). Tổng hoành độ và tung độ của điểm \(N\) bằng 3.
Giả sử kết quả khảo sát hai khu vực \(A\) và \(B\) về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:
Tuổi kết hôn | \([19;22)\) | \([22;25)\) | \([25;28)\) | \([28;31)\) | \([31;34)\) |
Số phụ nữ khu vực \(A\) | 10 | 27 | 31 | 25 | 7 |
Số phụ nữ khu vực \(B\) | 47 | 40 | 11 | 2 | 0 |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: \(15\) (tuổi).
b) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: \(12\)(tuổi).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm ứng với khu vực A là: \(\frac{{61}}{3}\) (tuổi).
d) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn.
Hằng ngày mực nước của một con kênh lên xuống theo thủy triều. Độ sâu \(h\,\,\left( {\rm{m}} \right)\) của mực nước trong kênh tại thời điểm \(t\,\,\left( {\rm{h}} \right)\,\,\left( {0 \le t \le 24} \right)\) trong ngày được xác định bởi công thức \(h = 2\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 5\). Gọi \(\left( {a\,;\,b} \right)\) là khoảng thời gian trong ngày mà độ sâu của mực nước trong kênh tăng dần. Tính giá trị của \(a + b\).
Một ông nông dân có \(240\)m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là bao nhiêu m2?
Một doanh nghiệp cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai máy \(A\) và \(B\). Máy \(A\) làm việc trong \(x\) ngày cho số tiền lãi là \({x^2} + 2x\) (triệu đồng), máy \(B\) làm việc trong \(y\) ngày cho số tiền lãi là \( - 27{y^2} + 326y\) (triệu đồng). Hỏi doanh nghiệp đó cần sử dụng máy \(A\) làm việc trong bao nhiêu ngày để số tiền lãi thu được nhiều nhất? Biết rằng hai máy \(A\) và \(B\) không đồng thời làm việc và máy \(B\) làm việc không quá 6 ngày.
Trong không gian tọa độ \(Oxyz\), gọi \(A,B,C\) lần lượt là hình chiếu của \[M\left( {3;3;3} \right)\] lên các trục tọa độ \(Ox,Oy,Oz\). Giả sử \[H\left( {a;b;c} \right)\]là trực tâm tam giác \(ABC\). Tính \[{a^2} + {b^2} + {c^2}\].
Cho tứ diện ABCD có \(AB = AC = AD = 1.\) và \[\widehat {BAC} = \widehat {BAD} = 60^\circ ,\,\widehat {CAD} = 90^\circ \]. Gọi \(I\) là điểm trên cạnh \(AB\) sao cho \(AI = 3IB\) và \(J\) là trung điểm của \(CD\). Tính độ dài đoạn thẳng \[IJ\]và làm tròn kết quả đến hàng phần trăm.
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị: Centimet) của 43 học sinh trong một lớp học khối 11 của một trường phổ thông
Nhóm | Giá trị đại diện | Tần số |
\(\left[ {150;155} \right)\) | 152,5 | 5 |
\(\left[ {155;160} \right)\) | 157,5 | 10 |
\(\left[ {160;165} \right)\) | 162,5 | 12 |
\(\left[ {165;170} \right)\) | 167,5 | 9 |
\(\left[ {170;175} \right)\) | 172,5 | 4 |
\(\left[ {175;180} \right)\) | 177,5 | 3 |
|
| \(n = 43\) |
Tính phương sai của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm).