62 câu hỏi
Số tâm đối xứng của đường tròn là:
\(1\).
\(2\).
\(3\).
\(4\).
Tâm đối xứng của đường tròn là:
Điểm bất kì bên trong đường tròn.
Điểm bất kì bên ngoài đường tròn.
Điểm bất kì trên đường tròn.
Tâm của đường tròn.
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
Đường tròn không có trục đối xứng.
Đường tròn có duy nhất một trục đối xứng là đường kính.
Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau.
Đường tròn có vô số trục đối xứng là đường kính.
Điền từ thích hợp vào chỗ trống: “Đường tròn có … trục đối xứng”.
\(1\).
\(2\).
Vô số.
\(3\).
Cho đường tròn \((O;R)\) và điểm \(M\) bất kỳ, biết rằng \(OM = R\). Chọn khẳng định đúng?
Điểm \(M\) nằm ngoài đường tròn.
Điểm \(M\) nằm trên đường tròn.
Điểm \(M\) nằm trong đường tròn.
Điểm \(M\) không thuộc đường tròn.
Cho đường tròn \((O;R)\) và điểm \(M\) bất kỳ, biết rằng \(OM > R\). Chọn khẳng định đúng?
Điểm \(M\) nằm ngoài đường tròn.
Điểm \(M\) nằm trên đường tròn.
Điểm \(M\) nằm trong đường tròn.
Điểm \(M\) không thuộc đường tròn.
Trên mặt phẳng toạ độ \(Oxy\), xác định vị trí tương đối của điểm \(A( - 1; - 1)\) và đường tròn tâm là gốc toạ độ \(O\), bán kính \(R = 2\).
Điểm \(A\) nằm ngoài đường tròn.
Điểm \(A\) nằm trên đường tròn.
Điểm \(A\) nằm trong đường tròn.
Không kết luận được.
Trên mặt phẳng toạ độ \(Oxy\), xác định vị trí tương đối của điểm \(A( - 3; - 4)\) và đường tròn tâm là gốc toạ độ \(O\), bán kính \(R = 3\).
Điểm \(A\) nằm ngoài đường tròn.
Điểm \(A\) nằm trên đường tròn.
Điểm \(A\) nằm trong đường tròn.
Không kết luận được.
Cho \(A\), \(B\) thuộc đường tròn \(\left( {O;R} \right)\), biết khoảng cách từ \(O\) đến \(AB\) bằng \(9\) và dây \(AB = 24\) cm. Bán kính \(R\) bằng
\(R = 15\)cm.
\(R = 12\) cm.
\(R = 9\)cm.
\(R = 20\)cm.
Cho đường tròn \(\left( {O;\sqrt 3 } \right)\) và dây \(AB\). Kẻ bán kính \(OC \bot AB\). Độ dài \(AB\) bằng bao nhiêu để \(ACBO\) là hình thoi?
\(\frac{{3\sqrt 3 }}{2}\).
\(2\sqrt 3 \).
\(3\).
\(5\).
Cho điểm \(A\) cố định trong đường tròn \(\left( {O,\,R} \right)\), \(A\) khác \(O\), điểm \(B\) chuyển động trên đường tròn. Chọn phương án đúng
Độ dài đoạn \(AB\) ngắn nhất là \(2R - OA\).
Độ dài đoạn \(AB\) ngắn nhất là \(R - OA\).
Độ dài đoạn \(AB\) dài nhất là \(2R\).
Độ dài đoạn \(AB\) dài nhất là \(2R - OA\).
Cho đường tròn \(\left( {O;5\,{\rm{cm}}} \right)\), hai dây \(AB = 8\,{\rm{cm}}\), \(CD = 6\,{\rm{cm}}\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(CD\). Chọn câu đúng
\(OM = 4\,{\rm{cm}}\).
\(ON = 4\,cm\).
\(OM > ON\).
\(OM = ON\).
Cho nửa đường tròn \(\left( {{\rm{O}}\,{\rm{;}}\,{\rm{R}}} \right)\) đường kính \(AB\), điểm \(M\) nằm trên dây \(AB\) sao cho \(AM = \frac{{2{\rm{R}}}}{5}\). Qua \(M\) kẻ dây cung \(CD\) vuông góc với \(AB\). Độ dài dây \(CD\) là
\(\frac{{8R}}{5}\).
\(\frac{{7{\rm{R}}}}{5}\).
\(\frac{{6{\rm{R}}}}{5}\).
\({\rm{R}}\).
Cho nửa đường tròn \(\left( {{\rm{O}}\,{\rm{;}}\,{\rm{R}}} \right)\) đường kính \(AB\), điểm \(C\) di chuyển trên nửa đường tròn, khi đó tích hai dây cung \(CA.CB\) lớn nhất là bao nhiêu?
\(\frac{{8R}}{5}\).
\(\frac{{7{\rm{R}}}}{5}\).
\(\frac{{6{\rm{R}}}}{5}\).
\({\rm{R}}\).
Cho nửa đường tròn \(\left( {{\rm{O}}\,{\rm{;}}\,{\rm{R}}} \right)\) đường kính \(AB\), điểm \(C\) di chuyển trên nửa đường tròn, khi đó tổng hai dây cung \(CA + CB\) lớn nhất là bao nhiêu?
\(3\sqrt 2 R\).
\(2\sqrt 2 R\).
\(2R\).
\(\sqrt 3 R\).
Cho đường tròn \(\left( {O\,;\,\,R} \right)\), điểm \(M\) cố định nằm trong đường tròn, \(OM = a\), dây \(AB\) bất kì qua \(M\). Khẳng định nào sau đây đúng?
Độ dài đoạn \(AB\) nhỏ nhất là \(2\sqrt {{R^2} - {a^2}} \)
Độ dài đoạn \(AB\) nhỏ nhất là \(\sqrt {{R^2} - {a^2}} \).
Độ dài đoạn \(AB\) lớn nhất là \(R + a\).
Độ dài đoạn \(AB\) lớn nhất là \(R + 2a\).
Cho đường tròn \(\left( {O\,;\,\,20\,cm} \right)\), hai dây \(AB\) và \(CD\) song song với nhau và cách nhau một đoạn bằng \(28\,cm\). Biết \(AB = 32\,cm\), khi đó độ dài đoạn \(CD\) bằng
\(22\,cm\).
\(24\,cm\).
\(26\,cm\).
\(28\,cm\).
Cho đường tròn \((O)\), đường kính \(AB\). Kẻ hai dây \(AC\) và \(BD\) song song. So sánh độ dài \(AC\) và \(BD\).
\(AC > BD\).
\(AC < BD\).
\(AC = BD\).
\(AC = 3BD\).
Cho đường tròn \((O;10cm)\). Dây \(AB\) và \(CD\) song song, có độ dài lần lượt là \(16cm\) và \(12cm\). Tính khoảng cách giữa hai dây
\(14cm\).
\(10cm\).
\(12cm\).
\(16cm\).
Cho đường tròn \((O)\) đường kính \(AB = 14cm\), dây \(CD\) có độ dài \(12cm\) vuông góc với \(AB\) tại \(H\) nằm giữa \(O\) và \(B\). Độ dài \(HA\) là:
\(7 + \sqrt {13} \,cm\)
\(7 - \sqrt {13} \,cm\).
\(7\,cm\).
\(7 - 2\sqrt {13} \,cm\).
Cho đường tròn \(\left( O \right)\) và dây \(AB\), \(M\) là điểm chính giữa của cung nhỏ \(AB\). Lấy điểm \(C\) thuộc đoạn \(AB\), đường thẳng \(MC\) cắt \(\left( O \right)\) tại \(D\). Cho \(MC = 9\,cm\), \(MD = 16\,cm\), độ dài dây cung \(MA\) là
\(25\,cm\).
\(20\,cm\).
\(12\,cm\).
\(10\,cm\).
Cho đường tròn \[\left( {O;R} \right)\], hai dây cung \[AB,\,CD\] vuông góc với nhau. Chọn phương án đúng?
\(A{D^2} + B{C^2} = 3{R^2}\).
\(A{D^2} + B{C^2} > 4{R^2}\).
\(A{D^2} + B{C^2} < 4{R^2}\).
\(A{D^2} + B{C^2} = 4{R^2}\).
Cho đường tròn \[\left( {O;R} \right)\], hai điểm \[A,\,B\] nằm trên đường tròn, \[\widehat {AOB} = 60^\circ \]. Dây cung \[CD\] cắt \[OA,\,OB\] lần lượt tại \[M,\,N\] sao cho \[CM = MN = ND\]. Hỏi độ dài đoạn \[CD\] bằng bao nhiêu?
\(R\sqrt 3 \).
\(R\).
\(\frac{R}{2}\).
\(\frac{R}{3}\).
Cho góc \[\widehat {AMB} = 50^\circ \] như hình vẽ. Khi đó khẳng định nào sau đây là đúng?
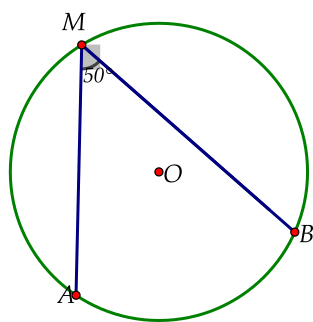
Số đo cung nhỏ là \[50^\circ \].
Góc \[\widehat {AMB}\] là góc ở tâm.
Số đo cung nhỏ là \[25^\circ \].
Số đo cung nhỏ là \[100^\circ \].
Cho \[\Delta OAB\] đều như trong hình vẽ sau, chọn khẳng định đúng.
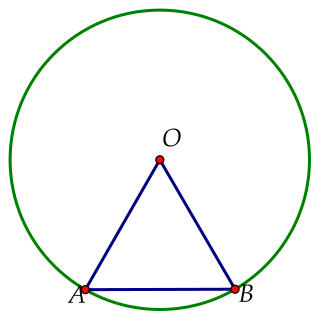
Số đo cung nhỏ \[AB\] là \[100^\circ \].
Số đo cung nhỏ \[AB\] là \[30^\circ \].
Số đo cung nhỏ \[AB\] là \[60^\circ \].
Số đo cung nhỏ \[AB\] là \[90^\circ \].
Cho hình thang cân \[ABCD\] nội tiếp đường tròn \[\left( O \right)\] có \[AB//CD\], \(\widehat {ADC} = 76^\circ \), \[\widehat {DAC} = 60^\circ \]. Khẳng định nào sau đây sai.
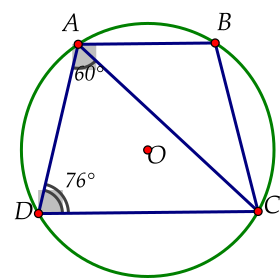
\(\widehat {BAC} = 44^\circ \).
Số đo cung nhỏ \[BC\] là \[88^\circ \].
Số đo cung nhỏ \[AD\] là \[88^\circ \].
Số đo cung nhỏ \[AC\] là \[104^\circ \].
Trên đường tròn \[\left( O \right)\] lấy hai điểm \[A\] và \[B\] sao cho \[\widehat {AOB} = 80^\circ \]. Vẽ dây \[AM\] vuông góc với bán kính \[OB\] tại \[H\]. Số đo cung nhỏ \[AM\] bằng
\[80^\circ \].
\[100^\circ \].
\[140^\circ \].
\[160^\circ \].
Cho đường tròn \(\left( {O;R} \right)\)và dây\(AB\) sao cho số đo cung lớn gấp ba lần số đo cung nhỏ . Số đo cung nhỏ là
\[90^\circ \].
\[60^\circ \].
\[120^\circ \].
\[150^\circ \].
Tìm số đo cung nhỏ \[AB\] và cung nhỏ \[CD\] qua hình vẽ sau
![Tìm số đo cung nhỏ \[AB\] và cung nhỏ \[CD\] qua hình vẽ sau (ảnh 1)](https://video.vietjack.com/upload2/images/1754926966/1754927034-image20.png)
sđ, sđ.
sđ, sđ.
sđ, sđ.
sđ, sđ.
Trên đường tròn \[\left( {O,R} \right)\] lấy hai điểm \[A\] và \[B\] sao cho số đo cung nhỏ \[AB\] bằng \[90^\circ \]. Độ dài dây cung \[AB\] bằng?
\[R\].
\[R\frac{{\sqrt 3 }}{2}\].
\[R\sqrt 2 \].
\[R\sqrt 3 \].
Đường thẳng \[m\] cắt đường tròn \[\left( {O;\,\,R} \right)\] tại hai điểm \[A,B\] sao cho \[AB = R\sqrt 3 \]. Số đo góc \[AOB\] bằng
\[150^\circ \].
\[120^\circ \].
\[90^\circ \].
\[60^\circ \].
Cho đường tròn \[\left( {O;R} \right)\], lấy điểm \[M\] nằm ngoài \[\left( O \right)\] sao cho \[OM = 2R\]. Từ \[M\] kẻ tiếp tuyến \[MA\] và \[MB\] với \[\left( O \right)\] (\[A,\,B\]là các tiếp điểm). Số đo cung \[AB\] nhỏ bằng
\[240^\circ \].
\[120^\circ \].
\[360^\circ \].
\[210^\circ \].
Cho \[\Delta ABC\] nội tiếp trong đường tròn \[\left( O \right)\]. Biết \[AB = a\]; \[\widehat {ACB} = 60^\circ \]. Bán kính của \[\left( O \right)\]là
\(\frac{a}{2}\).
\(\frac{{a\sqrt 3 }}{3}\).
\(a\).
\(2a\).
Hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';R'} \right)\] tiếp xúc ngoài tại \[A\]. Trên nửa mặt phẳng bờ \[OO'\] lấy \[B \in \left( O \right),\]\[C \in \left( {O'} \right)\] sao cho , . Hỏi góc \[BAC\] bằng bao nhiêu?
\[35^\circ \].
\[65^\circ \].
\[80^\circ \].
\[55^\circ \].
Cho nửa đường tròn \[\left( O \right)\] đường kính \[AB = 2R\]. Lấy \[M\] là điểm chính giữa cung \[AB\], hai điểm \[C\] và \[D\] di chuyển trên cung \[MA,MB\] sao cho \[CM//AD\]. Hỏi độ dài cạnh \[CD\] bằng bao nhiêu?
\[\frac{{2R}}{3}\].
\[R\sqrt 3 \].
\[\frac{{R\sqrt 3 }}{2}\].
\[R\sqrt 2 \].
Đường thẳng \(m\) cắt đường tròn \(\left( {O;R} \right)\)tại hai điểm \(A;\,B\)sao cho \(AB = R\sqrt 3 \). Số đo góc \(AOB\) bằng
\(150^\circ \).
\(120^\circ \).
\(90^\circ \).
\(60^\circ \).
Cho hình vẽ có đường thẳng \(xy\) tiếp xúc với \(\left( O \right)\) tại \(A\), sđ, sđ . Số đo góc \(BAC\) là
 .
.
\(50^\circ \).
\(65^\circ \).
\(80^\circ \).
\(90^\circ \).
Cho điểm \(A\) cố định trên \(\left( {O;R} \right)\), một góc nhọn \(\widehat {xAy}\) quay quanh điểm \(A\) sao cho hai tia \[Ax,Ay\] tương ứng cắt đường tròn tại hai điểm \(B,C\). Các đường cao đi từ \(B\) và \(C\) của tam giác \(ABC\) tương ứng cắt đường tròn tại \(D,E\). Biết \(\widehat {xAy} = \alpha \), số đo cung \(DAE\) là
\(360 - 4\alpha \).
\(180 - 2\alpha \).
\(2\alpha \).
\(90 + \alpha \).
Cho nửa đường tròn \(\left( O \right)\)đường kính \(AB = 2R\). Lấy \(M\) là điểm chính giữa cung \(AB\), hai điểm \(C,D\) di chuyển trên cung \(MA,MB\) sao cho \(CM{\rm{//}}AD\). Hỏi độ dài cạnh \(CD\) bằng bao nhiêu?
\(\frac{{2R}}{3}\).
\(R\sqrt 3 \).
\(\frac{{R\sqrt 3 }}{2}\).
\(R\sqrt 2 \).
Hai đường tròn \[\left( {O\,;\,R} \right)\] và \[\left( {O'\,;\,R'} \right)\] tiếp xúc ngoài tại \[A\]. Trên nửa mặt phẳng bờ \[{\rm{OO'}}\] lấy \[{\rm{B}} \in \left( O \right)\,,\,C \in \left( {O'} \right)\] sao cho sđ, sđ. Hỏi góc \[BAC\] bằng bao nhiêu?
\(35^\circ \).
\(65^\circ \).
\(80^\circ \).
\[55^\circ \].
Trên đường tròn \(\left( {O;R} \right)\)lấy các điểm \(A,B,C,D\)theo chiều kim đồng hồ sao cho ,, . Hỏi chu vi tứ giác \(ABCD\)bằng bao nhiêu?
\(R\left( {1 + 2\sqrt 2 + \sqrt 3 } \right)\).
\(R\left( {1 + \sqrt 2 + \sqrt 3 } \right)\).
\(R\left( {1 + 2\sqrt 2 + 2\sqrt 3 } \right)\).
\(R\left( {1 + \sqrt 2 + 2\sqrt 3 } \right)\).
Một hình tròn có chu vi \[20\,{\rm{cm}}\]. Diện tích của hình tròn đó xấp xỉ bằng
\(31,8\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(63,7\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(127,3\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(314,2\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Cung \(AB\) của một đường tròn bán kính \(R\) có độ dài \(\frac{{\pi R}}{6}\). Số đo cung \(AB\) bằng
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
\(60^\circ \).
Một tam giác đều có cạnh bằng \(2\,{\rm{cm}}\). Độ dài đường tròn ngoại tiếp tam giác đều đó bằng
\(\frac{{2\pi }}{{\sqrt 3 }}\,{\rm{cm}}\).
\(\frac{{4\pi }}{3}\,{\rm{cm}}\).
\(\frac{{2\pi }}{3}\,{\rm{cm}}\).
\(\frac{{4\pi }}{{\sqrt 3 }}\,{\rm{cm}}\).
Diện tích hình viên phân có bán kính \(R\), số đo cung bằng \(90^\circ \) là
\(\frac{{\pi {R^2}}}{4}\).
\(\frac{{\left( {\pi - 1} \right){R^2}}}{2}\).
\(\frac{{\left( {\pi - 2} \right){R^2}}}{4}\).
\(\frac{{{R^2}}}{2}\).
Một vườn hoa hình tròn có bán kính \(OA = 5\,{\rm{m}}\). Ở phía ngoài vườn ta làm một lối đi xung quanh hình vành khăn. Biết diện tích của lối đi bằng diện tích của vườn hoa. Chiều rộng \(AB\) của lối đi xấp xỉ bằng
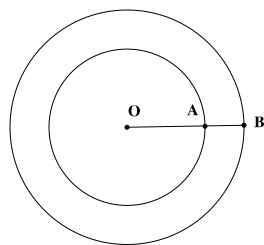
\(4,3\,{\rm{m}}\).
\(2,1\,{\rm{m}}\).
\(2,5\,{\rm{m}}\).
\(3,5\,{\rm{m}}\).
Cho hình tròn có đường kính bằng \[8\]cm. Chu vi của hình tròn đó xấp xỉ bằng
\(16,0\)cm.
\(25,1\)cm.
\(24,0\)cm.
\[50,3\]cm.
Độ dài cung tròn có số đo \[60^\circ \], bán kính \(R\) là
\(\frac{{\pi R}}{3}\).
\(\frac{{\pi R}}{2}\).
\(\frac{{\pi R}}{6}\).
\(\frac{{\pi R}}{4}\).
Cung \[AB\] của một đường tròn bán kính \[R\] có độ dài bằng \(\frac{{\pi R}}{4}\). Số đo cung \[AB\] bằng
\(30^\circ \).
\(45^\circ \).
\(60^\circ \).
\(90^\circ \).
Diện tích hình tròn có đường kính bằng \[8\]cm xấp xỉ bằng
\(25,1c{m^2}\).
\(16,0c{m^2}\).
\(50,3c{m^2}\).
\(39,5c{m^2}\).
Một hình tròn có chu vi bằng \[6\pi \,dm\]. Diện tích của hình tròn đó bằng
\(9\pi \,d{m^2}\).
\(12\pi \,d{m^2}\).
\(18\pi \,d{m^2}\).
\(36\pi \,d{m^2}\).
Một hình quạt tròn có bán kính \[R\], độ dài cung bằng đường kính. Diện tích của hình quạt đó là
\({R^2}\).
\(\frac{{{R^2}}}{2}\).
\(\frac{{\pi {R^2}}}{2}\).
\(\frac{{\pi {R^2}}}{4}\).
Độ dài cung \[AB\] của đường tròn \[\left( {O;\,R} \right)\] bằng \[R\]. Số đo góc \[AOB\] xấp xỉ bằng
\(57^\circ 18'\).
\(28^\circ 39'\).
\(32^\circ 42'\).
\(61^\circ 21'\).
Chọn phát biểu sai.
Diện tích hình tròn tỉ lệ thuận với bình phương bán kính của nó.
Độ dài cung của đường tròn tỉ lệ thuận với số đo góc của cung.
Chu vi hình tròn tỉ lệ thuận với bình phương bán kính của nó.
Diện tích hình quạt tròn tỉ lệ thuận với độ dài cung của hình quạt.
Diện tích của hình tròn thay đổi như thế nào nếu tăng bán kính của nó lên \(3\) lần?
Tăng \(3\) lần.
Tăng \(6\) lần.
Tăng \(9\) lần.
Tăng \(12\) lần.
Độ dài cung của đường tròn thay đổi như thế nào nếu giảm số đo góc của cung đi \(2\)lần?
Giảm \(2\) lần.
Giảm \(4\) lần.
Giảm \(6\) lần.
Giảm \(8\) lần.
Một hình vuông có cạnh bằng \(a\). Độ dài đường tròn ngoại tiếp hình vuông đó bằng
\(2\pi a\).
\(\frac{{\sqrt 2 }}{2}\pi a\).
\(\sqrt 2 \pi a\).
\(2\sqrt 2 \pi a\).
Một sân vận động có đường chạy đua dài \(400\)m. đường chạy gồm các đoạn \(AB,CD\)là chiều dài của hình chữ nhật \(ABCD\)và hai nửa đường tròn. Biết \(AB = 100\)m, độ dài \(BC\) xấp xỉ bằng
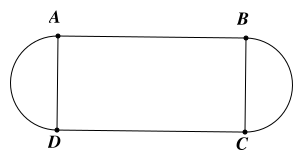
\(50\)m.
\(63,7\)m.
\(31,8\)m.
\(78,5\)m.
Cho hình vuông \(ABCD\)cạnh \(a\). Vẽ bốn cung phần tư đường tròn nằm trong hình vuông có tâm theo thứ tự là \(A,B,C,D\)và bán kính bằng \(a\),ta được một hình hoa bốn cánh. Chu vi của hình hoa đó bằng
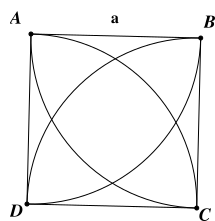
\(\frac{2}{3}\pi a\).
\(\pi a\).
\(\frac{1}{3}\pi a\).
\(\frac{4}{3}\pi a\).
Diện tích hình viên phân có bán kính \(20cm\), số đo cung \(120^\circ \) bằng khoảng
\(123\,{\rm{c}}{{\rm{m}}^2}\).
\(332\,{\rm{c}}{{\rm{m}}^2}\).
\(246\,{\rm{c}}{{\rm{m}}^2}\).
\(665\,{\rm{c}}{{\rm{m}}^2}\).
Cho đường tròn \(\left( O \right)\) đường kính \(AB = 2R\), \[C\] là điểm chính giữa của cung \[AB\]. Cung có tâm \[C\], bán kính \[CA\]. Diện tích phần tô đậm bằng
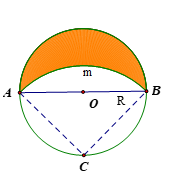
\({R^2}\).
\(\frac{{\pi {R^2}}}{4}\).
\(\frac{{\pi {R^2}}}{3}\).
\(\frac{{3{R^2}}}{4}\).
Cho tam giác đều \(ABC\) cạnh \(20cm\). Các nửa đường tròn đường kính \(AB\), \(BC\), \(CA\) tạo thành một hình hoa ba cánh có diện tích xấp xỉ bằng
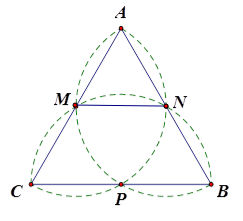
\(141,0c{m^2}\).
\(173,2c{m^2}\).
\(227,6c{m^2}\).
\(541,7c{m^2}\).
