46 CÂU HỎI
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số \[y = a{x^2}\]với \(a \ne 0\).
Đồ thị hàm số nhận trục tung làm trục đối xứng.
Với \[a > 0\] đồ thị nằm phía trên trục hoành và \[O\] là điểm cao nhất của đồ thị.
Với \[a < 0\] đồ thị nằm phía dưới trục hoành và \[O\] là điểm cao nhất của đồ thị.
>
Với \[a > 0\] đồ thị nằm phía trên trục hoành và \[O\] là điểm thấp nhất của đồ thị.
Giá trị của hàm số \[y = f(x) = - 7{x^2}\] tại \[{x_0} = - 2\] là:
\[28\].
\[14\].
\[21\].
\[ - 28\].
Giá trị của hàm số \[y = f(x) = \frac{4}{5}{x^2}\] tại \[{x_0} = - 5\] là
\[20\].
\[10\].
\[4\].
\[ - 20\].
Cho hàm số \[y = f(x) = ( - 2m + 1){x^2}\]. Tìm giá trị của \[m\] để đồ thị đi qua điểm \[A( - 2;4)\].
\[m = 0\].
\[m = 1\].
\[m = 2\].
\[m = - 2\].
Cho hàm số \[y = f(x) = \frac{{2m - 3}}{3}{x^2}\]. Tìm giá trị của \[m\] để đồ thị đi qua điểm \[B( - 3;5)\]
\[m = 1\].
\[m = \frac{3}{7}\].
\[m = \frac{7}{3}\].
\[m = 3\].
Trong các điểm \(A(1;2);B( - 1; - 1);C(10; - 200);D(\sqrt {10} ; - 10)\) có bao nhiêu điểm thuộc đồ thị hàm số \[y = - {x^2}\].
\(1\).
\(4\).
\(3\).
\(2\).
Cho hàm số \[y = ( - {m^2} + 4m - 5){x^2}\]. Kết luận nào sau đây là đúng
Đồ thị của hàm số nằm phía trên trục hoành.
Đồ thị của hàm số nhận gốc tọa độ \[O\] là điểm cao nhất.
Hàm số nhận Ox làm trục đối xứng
Đồ thị hàm số là một đường thẳng.
Cho hàm số \[y = (4{m^2} + 12m + 11){x^2}\]. Kết luận nào sau đây là sai?
Đồ thị của hàm số nằm phía dưới trục hoành.
Đồ thị của hàm số nhận gốc tọa độ \[O\] là điểm thấp nhất.
Hàm số nhận Ox làm trục đối xứng.
Đồ thị hàm số là một đường thẳng.
Cho hàm số \[y = (2m + 2){x^2}\]. Tìm \[m\] để đồ thị hàm số đi qua điểm \(A(x;y)\) với \((x;y)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\)
\[m = \frac{7}{4}\].
\[m = \frac{1}{4}\].
\[m = \frac{7}{8}\].
\[m = - \frac{7}{8}\].
Cho hàm số \[y = ( - 3m + 1){x^2}\]. Tìm \[m\] để đồ thị hàm số đi qua điểm \(A(x;y)\) với \((x;y)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x - 3y = - 2\\x - 2y = - 3\end{array} \right.\)
\[m = \frac{1}{3}\].
\[m = - \frac{1}{3}\].
\[m = 3\].
\[m = - 3\].
Hình vẽ dưới đây là của đồ thị hàm số nào?
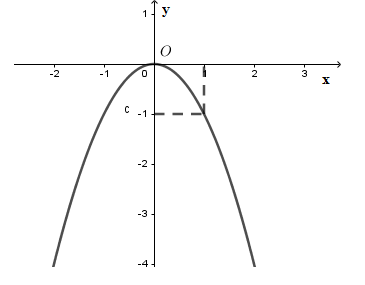
\[y = - {x^2}\].
\[y = {x^2}\].
\[y = 2{x^2}\].
\[y = - 2{x^2}\].
Hình vẽ dưới đây là của đồ thị hàm số nào?
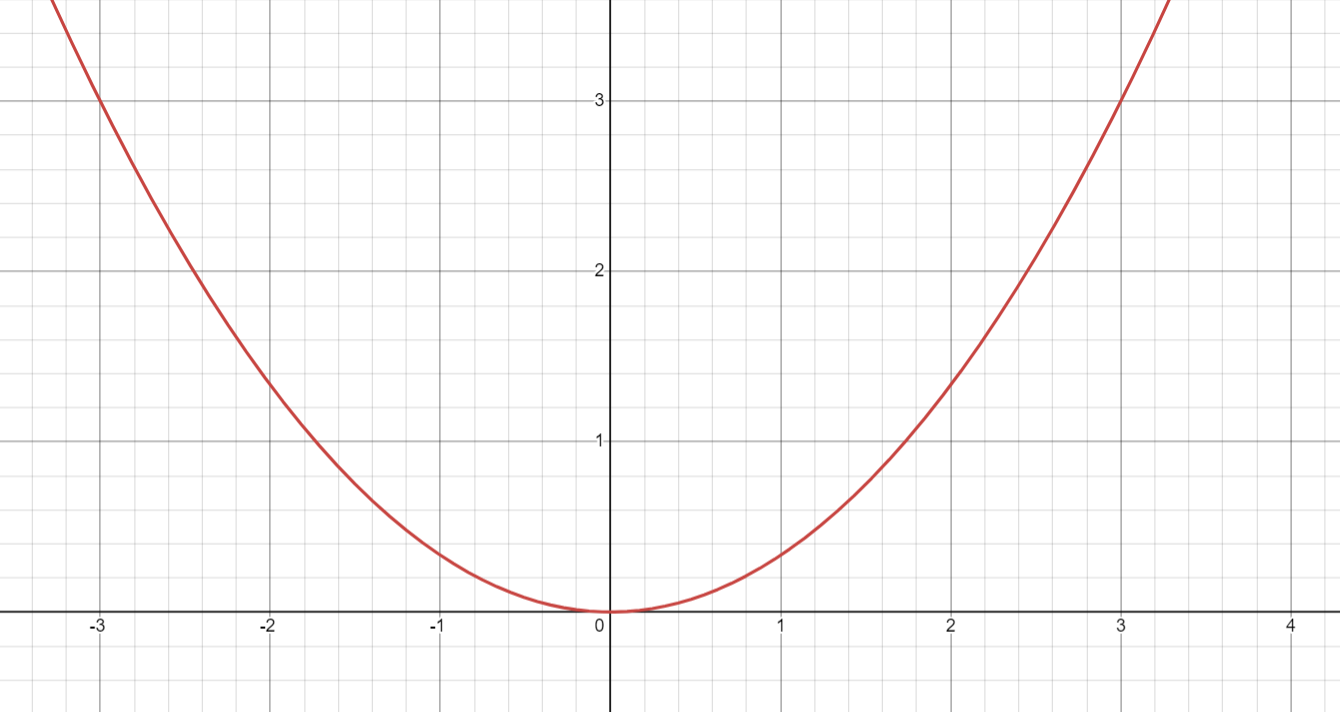
\[y = {x^2}\].
\[y = \frac{1}{2}{x^2}\].
\[y = 3{x^2}\].
\[y = \frac{1}{3}{x^2}\].
Cho hàm số \(y = \sqrt 3 {x^2}\) có đồ thị là \((P)\). Có bao nhiêu điểm trên \((P)\)có tung độ gấp đôi hoành độ.
\[5\].
\[4\].
\[3\].
\[2\].
Cho hàm số \[y = - \frac{2}{5}{x^2}\] có đồ thị là \((P)\). Điểm trên \((P)\) (khác gốc tọa độ \(O(0;0)\)) có tung độ gấp ba lần hoành độ thì có hoành độ là:
\[\frac{{15}}{2}\].
\[\frac{{ - 15}}{2}\].
\[\frac{2}{{15}}\].
\[ - \frac{2}{{15}}\].
Cho parabol. \[y = \frac{1}{4}{x^2}\] Xác định \[m\] để điểm \(A(\sqrt 2 ;m)\) nằm trên parabol.
\[m = \frac{1}{2}\].
\[m = - \frac{1}{2}\].
\[m = 2\].
\[m = - 2\].
Cho parabol \[y = - \sqrt 5 {x^2}\]. Xác định \[m\] để điểm \(A\left( {m\sqrt 5 ; - 2\sqrt 5 } \right)\) nằm trên parabol.
\[m = - \frac{5}{2}\].
\[m = \frac{2}{5}\].
\[m = \frac{5}{2}\].
\[m = - \frac{2}{5}\].
Cho \[(P):\,\,\,\,y = \frac{1}{2}{x^2};(d):\,\,\,\,y = x - \frac{1}{2}\]. Tìm tọa độ giao điểm của \((P)\) và \((d)\)
\[\left( {1;\frac{1}{2}} \right)\].
\[(1;2)\].
\[\left( {\frac{1}{2};1} \right)\].
\[(2;1)\].
Cho \[(P):\,\,\,\,y = 3{x^2};(d):\,\,\,\,y = - 4x - 1\]. Tìm tọa độ giao điểm \((P)\)và \((d)\)
\[\left( {\frac{1}{3}; - \frac{1}{3}} \right);(1;3)\].
\[\left( {\frac{1}{3};\frac{1}{3}} \right);(1;3)\].
\[\left( { - \frac{1}{3};\frac{1}{3}} \right);( - 1;3)\].
\[\left( { - \frac{1}{3};\frac{1}{3}} \right)\].
Cho parabol \[(P):y = {x^2}\] và \[d:y = 2x + 3.\] Tìm tọa độ giao điểm \(A,B\) của \((P)\) và \(d\).
\[A( - 1; - 1);B(3; - 9)\].
\[A( - 1;1);B( - 3;9)\].
\[A( - 1;1);B(3;9)\].
\[A( - 1; - 1);B(3;9)\].
Cho parabol \[(P):y = {x^2}\] và \[d:y = 4x + 5\]. Tìm tọa độ giao điểm \(A,B\) của \((P)\) và \(d\).
\[A( - 1;1);B(5;25)\].
\[A( - 1;1);B( - 5;25)\].
\[A(1;1);B(5;25)\].
\[A( - 1; - 1);B( - 5; - 25)\].
Cho parrabol \((P):y = (m - 1){x^2}\) và đường thẳng \((d):y = 3 - 2x\). Tìm \[m\] để đường thẳng \[d\] cắt \((P)\) tại điểm có tung độ \(y = 5\).
\[m = 5\].
\[m = 7\].
\[m = 6\].
\[m = - 6\].
Cho parrabol \((P):y = \sqrt {5m + 1} .{x^2}\) và đường thẳng \((d):y = 5x + 4\). Tìm \[m\] để đường thẳng \[d\] cắt \((P)\) tại điểm có tung độ \(y = 9\).
\[m = 5\].
\[m = 15\].
\[m = 6\].
\[m = 16\].
Cho parrabol \((P):y = \left( {\frac{{1 - 2m}}{m}} \right).{x^2}\) và đường thẳng \((d):y = 2x + 2\). Biết đường thẳng \[d\] cắt 
tại một điểm có tung độ \(y = 4\). Tìm hoành độ giao điểm còn lại của \[d\] và parabol \((P)\)
\[x = - \frac{1}{2}\].
\[x = \frac{1}{2}\].
\[x = - \frac{1}{4}\].
\[x = \frac{1}{4}\].
Trong mặt phẳng toạ độ 
, biết điểm có hoành độ bằng 1 là một điểm chung của parabol \(y = 2{x^2}\,\,\) và đường thẳng \(y = (m - 1)x - 2\), với 
là tham số. Khi đó giá trị của 
.
\(m = 1\)
\(m = 5\)
\(m = 2\)
\(m = 3\)
Cho hàm số \(y = {x^2}\,\,\)có có đồ thị là (P). Đường thẳng đi qua 2 điểm thuộc (P) có hoành độ bằng \[ - 1\] và 2 là:
\(y = - x + 2\)
\(y = x + 2\)
\(y = - x - 2\)
\(y = x - 2\)
Cho hàm số \(y = - 2{x^2}\,\,\) có đồ thị là (P). Toạ độ các điểm thuộc (P) có tung độ bằng -6 là
A. \(\left( {\sqrt {3;} - 6} \right);\left( { - \sqrt {3;} - 6} \right)\)
B. \(\left( { - 6;\sqrt 3 } \right);\left( { - 6; - \sqrt 3 } \right)\)
C. \(\left( {\sqrt {3;} - 6} \right).\)
D. \(( - 72; - 6)\)
Hàm số \(y = ({m^2} + 3m - 3){x^2};({m^2} + 3m - 3 \ne 0)\). Tổng các giá trị của \(m\) biết đồ thị của hàm số đi qua điểm \(A( - 1;1)\).
1
\[ - 1\]
\[ - 3\]
3
Cho parabol \(\left( P \right):y = \frac{1}{2}{x^2}\)cắt đường thẳng \(\left( d \right):y = x + \frac{3}{2}\)
tại hai điểm phân biệt A vàB. Độ dài đoạn thẳng AB bằng
\(4\sqrt 2 \)
\(5\sqrt 3 \).
4
\(2\sqrt 2 \)
Số giao điểm của đường thẳng \(d:y = 2x + 4\) và parabol \((P):y = {x^2}\) là:
\(2\).
\(1\).
\(0\).
\(3\).
Tìm tham số \[m\] để đường thẳng \(d:y = \frac{1}{2}x + m\) tiếp xúc với parabol \[(P):y = \frac{{{x^2}}}{2}\].
\[m = \frac{1}{4}\].
\[m = - \frac{1}{4}\].
\[m = \frac{1}{8}\].
\[m = - \frac{1}{8}\].
Tìm tham số \[m\] để đường thẳng \[d:y = mx + 2\] cắt parabol \[(P):y = \frac{{{x^2}}}{2}\] tại hai điểm phân biệt.
\[m = 2\].
\[m = - 2\].
\[m = 4\].
\[m \in \mathbb{R}\].
Tìm tham số \[m\] để đường thẳng \[d:y = - 2(m + 1)x + \frac{1}{2}{m^2}\] cắt parabol \[(P):y = - 2{x^2}\] tại hai điểm phân biệt.
\[m > - \frac{1}{2}\].
\[m = \frac{1}{2}\].
\[m = \frac{1}{4}\].
\[m > - 2\].
Tìm tham số \[m\] để đường thẳng \[d:y = 2x + m\] và parabol \[(P):y = 2{x^2}\] không có điểm chung.
\(m < - \frac{1}{2}\).
>
\[m \le - \frac{1}{2}\].
\[m > \frac{1}{2}\].
\[m \ge \frac{1}{2}\].
Tìm tham số \[m\] để đường thẳng \[d:y = \frac{m}{2}x - \frac{{{m^2}}}{8} - m + 1\] và parabol \[(P):y = \frac{1}{2}{x^2}\] không có điểm chung.
\(m < - 1\).
>
\[m \le 1\].
\[m > 1\].
\[m < 1\].
>
Tìm tham số \[m\] để đường thẳng \[d:y = (m - 2)x + 3m\] và parabol \[(P):y = {x^2}\] cắt nhau tại hai điểm phân biệt nằm hai phía trục tung.
\(m < 3\).
>
\[m > 3\].
\[m > 2\].
\[m > 0\].
Cho parabol \[(P):y = {x^2}\] và đường thẳng \[d:y = (m + 2)x - m - 1\]. Tìm \[m\] để cắt tại hai điểm phân biệt nằm về hai phía trục tung.
\(m < - 1\).
>
\(m < - 2\).
>
\[m > - 1\].
\( - 2 < m < - 1\).
>
Có bao nhiêu giá trị của tham số \(m\) để đường thẳng \[d:y = 2mx - 4\] và parabol \[(P):y = {x^2}\]cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thỏa mãn \[\frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} = - 3\].
\(1\).
\(2\).
\(3\).
\(0\).
Có bao nhiêu giá trị của tham số \(m\) để đường thẳng \[d:y = 5x - m - 4\] và parabol \[(P):y = {x^2}\]cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thỏa mãn \[\frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} = 5\].
\(1\).
\(2\).
\(3\).
\(0\).
Cho parabol \[(P):y = {x^2}\] và \[d:y = 2x + 3\]. Với giao điểm \(A,B\) của \[(P)\]và \[d\] ở câu trước. Gọi \(C,D\)lần lượt là hình chiếu vuông góc của \(A,B\) lên \(Ox\). Tính diện tích tứ giác \(ABCD\).
\[{S_{ABDC}} = 20{\mkern 1mu} {\mkern 1mu} \](đvdt).
\[{S_{ABDC}} = 40{\mkern 1mu} \](đvdt).
\[{S_{ABDC}} = 10{\mkern 1mu} {\mkern 1mu} \](đvdt).
\[{S_{ABDC}} = 30{\mkern 1mu} {\mkern 1mu} \](đvdt).
Cho parabol \[(P):y = {x^2}\]và \[d:y = 4x + 5\].Với giao điểm A,B của \((P)\) và \(d\) ở ý trước. Gọi lần lượt là hình chiếu vuông góc của \(A,B\) lên \(Ox\). Tính diện tích tứ giác \(ABCD\).
\[{S_{ABDC}} = 78{\mkern 1mu} {\mkern 1mu} \].
\[{S_{ABDC}} = 156\].
\[{S_{ABDC}} = 39{\mkern 1mu} {\mkern 1mu} \].
\[{S_{ABDC}} = 30{\mkern 1mu} {\mkern 1mu} \].
Có bao nhiêu giá trị của tham số \(m\) để đường thẳng \(d:y = - \frac{1}{2}x + m\) và parabol \((P):y = - \frac{1}{4}{x^2}\) cắt nhau tại hai điểm phân biệt có hoành độ \[{x_1};{x_2}\] thỏa mãn\[3{x_1} + 5{x_2} = 5\].
\[m = - \frac{5}{{16}}\].
\[m = \frac{5}{{16}}\].
\[m = - \frac{5}{4}\].
\[m = \frac{5}{4}\].
Cho parabol \((P):y = a{x^2}(a \ne 0)\) đi qua điểm \(A( - 2;4)\) và tiếp xúc với đồ thị \((d)\) của hàm số \[y = 2(m - 1)x + (m - 1)\]. Tọa độ tiếp điểm là:
\[(0;0)\].
\((1;1)\).
A và B đúng.
Đáp án khác.
Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = \left( {m + 1} \right)x - m\) (\(m\) là tham số). Tập hợp các giá trị của \(m\) để đường thẳng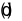 
cắt parabol 
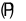tại hai điểm phân biệt có hoành độ\({x_1};{x_2}\)thoả mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 2022\) là
A. \(\left\{ { - 2020;2020} \right\}\)
B. \(\left\{ { - 2020; - 2021} \right\}\)
C. \(\left\{ { - 2020;2021} \right\}\)
D. \(\left\{ { - 2021;2021} \right\}\)
Cho parrabol \((P):y = \left( {\sqrt {3m + 4} - \frac{7}{4}} \right){x^2}\) và đường thẳng \((d):y = 3x - 5\). Biết đường thẳng \[d\] cắt 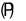tại một điểm có tung độ \(y = 1\). Tìm \(m\) và hoành độ giao điểm còn lại của 
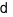và parabol \((P)\)
\[m = 0;x = 2\].
\[m = \frac{1}{4};x = - 10\].
\[m = 2;x = 8\].
\[m = 0;x = 10\].
Cho đồ thị hàm số \[y = 2{x^2}\] như hình vẽ. Dựa vào đồ thị, tìm \[m\] để phương trình \[2{x^2} - m - 5 = 0\] có hai nghiệm phân biệt.
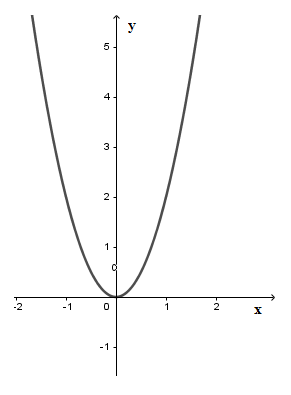
\[m < - 5\].
>
\[m > 0\].
\(m < 0\).
>
\[m > - 5\].
Cho đồ thị hàm số \(y = \frac{1}{2}{x^2}\left( P \right)\) như hình vẽ. Dựa vào đồ thị, tìm \(m\) để phương trình \({x^2} - 2m + 4 = 0\) có hai nghiệm phân biệt.
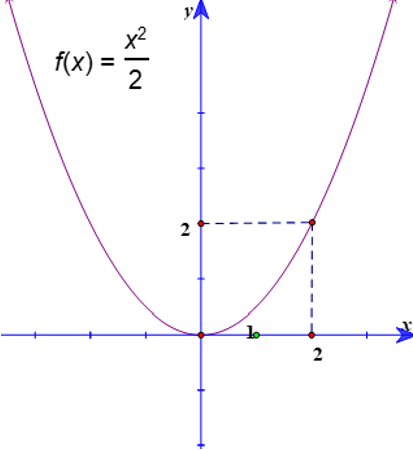
\(m > 2\).
\(m > 0\).
\(m < 2\).
>
\(m > - 2\).