103 câu hỏi
Cho các hình: Hình thang cân, hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều, hình bình hành. Có bao nhiêu hình là đa giác đều?
\(5\).
\(4\).
\(3\).
\(2\).
Cho các hình: Hình thang cân, hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều, hình bình hành. Có bao nhiêu hình là đa giác đều?
A. \(5\).
B. \(4\).
C. \(3\).
D. \(2\).
Cho các hình: Hình thang cân, hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều, hình bình hành. Có bao nhiêu hình là đa giác đều?
A. \(5\).
B. \(4\).
C. \(3\).
D. \(2\).
Biết độ dài các cạnh của mỗi tam giác trong các hình sau là bằng nhau, có tất cả bao nhiêu tam giác đều?
\(5\).
\(4\).
\(3\).
\(6\).
Biết độ dài các cạnh của mỗi tam giác trong các hình sau là bằng nhau, có tất cả bao nhiêu tam giác đều?
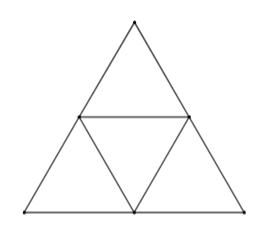
A. \(5\).
B. \(4\).
C. \(3\).
D. \(6\).
Biết độ dài các cạnh của mỗi tam giác trong các hình sau là bằng nhau, có tất cả bao nhiêu tam giác đều?
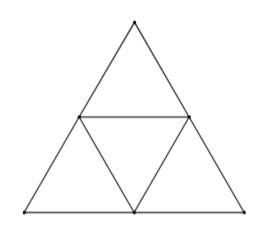
A. \(5\).
B. \(4\).
C. \(3\).
D. \(6\).
Cho các hình vẽ sau. Hình nào là lục giác đều
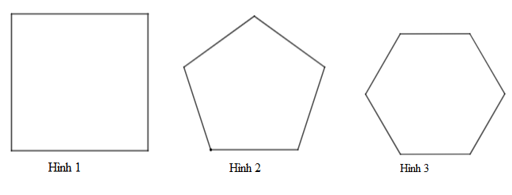
Hình 3.
Hình 2.
Hình 1.
Cả 3 hình.
Cho các hình vẽ sau. Hình nào là lục giác đều
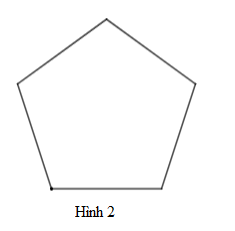
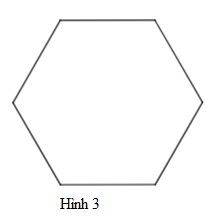
A. Hình 3.
B. Hình 2.
C. Hình 1.
D. Cả 3 hình.
Cho các hình vẽ sau. Hình nào là lục giác đều
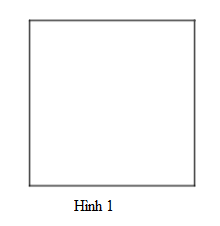
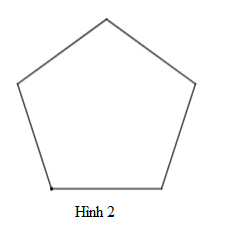
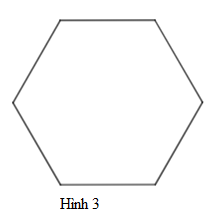
A. Hình 3.
B. Hình 2.
C. Hình 1.
D. Cả 3 hình.
Cho các hình vẽ sau. Hình nào là ngũ giác đều
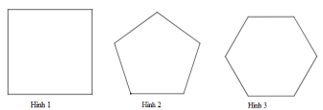
Hình 3.
Hình 2.
Hình 1.
Cả 3 hình.
Cho các hình vẽ sau. Hình nào là ngũ giác đều



A. Hình 3.
B. Hình 2.
C. Hình 1.
D. Cả 3 hình.
Cho các hình vẽ sau. Hình nào là ngũ giác đều



A. Hình 3.
B. Hình 2.
C. Hình 1.
D. Cả 3 hình.
Trong các khẳng định sau khẳng định đúng là
Hình vuông là đa giác đều
Hình thoi là đa giác đều
Hình chữ nhật là đa giác đều.
Hình thang cân là đa giác đều.
Trong các khẳng định sau khẳng định đúng là
A. Hình vuông là đa giác đều
B. Hình thoi là đa giác đều
C. Hình chữ nhật là đa giác đều.
D. Hình thang cân là đa giác đều.
Trong các khẳng định sau khẳng định đúng là
A. Hình vuông là đa giác đều
B. Hình thoi là đa giác đều
C. Hình chữ nhật là đa giác đều.
D. Hình thang cân là đa giác đều.
Cho hình vẽ cách viết tên nào sau đây đúng
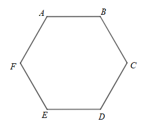
\(ABCDEF\).
\(ABCFED\).
\(AFBCDE\).
\(ACEFDB\).
Cho hình vẽ cách viết tên nào sau đây đúng
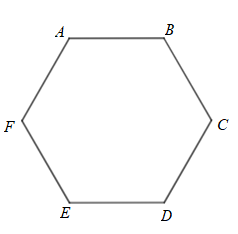
A. \(ABCDEF\).
B. \(ABCFED\).
C. \(AFBCDE\).
D. \(ACEFDB\).
Cho hình vẽ cách viết tên nào sau đây đúng
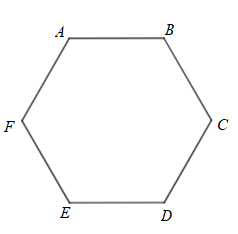
A. \(ABCDEF\).
B. \(ABCFED\).
C. \(AFBCDE\).
D. \(ACEFDB\).
Cho đa giác đều \[8\] cạnh, số đường chéo của đa giác đó là
\(40\).
\(28\).
\(20\).
\(16\).
Cho đa giác đều \[8\] cạnh, số đường chéo của đa giác đó là
A. \(40\).
B. \(28\).
C. \(20\).
D. \(16\).
Cho đa giác đều \[8\] cạnh, số đường chéo của đa giác đó là
A. \(40\).
B. \(28\).
C. \(20\).
D. \(16\).
Cho đa giác đều \[9\] cạnh, số đường chéo của đa giác đó là
\(36\).
\(27\).
\(20\).
\(18\).
Mỗi góc trong của lục giác đều là
A. \(120^\circ \).
B. \(150^\circ \).
C. \(90^\circ \).
D. \(135^\circ \).
Mỗi góc trong của lục giác đều là
A. \(120^\circ \).
B. \(150^\circ \).
C. \(90^\circ \).
D. \(135^\circ \).
Mỗi góc trong của lục giác đều là
\(120^\circ \).
\(150^\circ \).
\(90^\circ \).
\(135^\circ \).
Tổng số đo các góc của đa giác đều \[7\] cạnh là
A. \(900^\circ \).
B. \(540^\circ \).
C. \(1080^\circ \).
D. \(108^\circ \).
Tổng số đo các góc của đa giác đều \[7\] cạnh là
A. \(900^\circ \).
B. \(540^\circ \).
C. \(1080^\circ \).
D. \(108^\circ \).
Tổng số đo các góc của đa giác đều \[7\] cạnh là
\(900^\circ \).
\(540^\circ \).
\(1080^\circ \).
\(108^\circ \).
Tổng số đo các góc của đa giác đều \[9\] cạnh là
A. \(900^\circ \).
B. \(1026^\circ \).
C. \(1080^\circ \).
D. \(1260^\circ \).
Tổng số đo các góc của đa giác đều \[9\] cạnh là
A. \(900^\circ \).
B. \(1026^\circ \).
C. \(1080^\circ \).
D. \(1260^\circ \).
Tổng số đo các góc của đa giác đều \[9\] cạnh là
\(900^\circ \).
\(1026^\circ \).
\(1080^\circ \).
\(1260^\circ \).
Mỗi góc trong của đa giác đều \(n\) cạnh là
A. \(\left( {n - 1} \right)\,\,.\,\,180^\circ \).
B. \(\left( {n - 2} \right)\,\,.\,\,180^\circ \).
C. \(\frac{{\left( {n - 2} \right)\,\,.\,\,180^\circ }}{2}\).
D. \(\frac{{\left( {n - 2} \right)\,\,.\,\,180^\circ }}{n}\).
Mỗi góc trong của đa giác đều \(n\) cạnh là
A. \(\left( {n - 1} \right)\,\,.\,\,180^\circ \).
B. \(\left( {n - 2} \right)\,\,.\,\,180^\circ \).
C. \(\frac{{\left( {n - 2} \right)\,\,.\,\,180^\circ }}{2}\).
D. \(\frac{{\left( {n - 2} \right)\,\,.\,\,180^\circ }}{n}\).
Mỗi góc trong của đa giác đều \(n\) cạnh là
\(\left( {n - 1} \right)\,\,.\,\,180^\circ \).
\(\left( {n - 2} \right)\,\,.\,\,180^\circ \).
\(\frac{{\left( {n - 2} \right)\,\,.\,\,180^\circ }}{2}\).
\(\frac{{\left( {n - 2} \right)\,\,.\,\,180^\circ }}{n}\).
Tổng số đo các góc trong của đa giác đều \[n\] cạnh là \(1440^\circ \) thì số cạnh \[n\] là
A. \(9\).
B. \(10\).
C. \(7\).
D. \(8\).
Tổng số đo các góc trong của đa giác đều \[n\] cạnh là \(1440^\circ \) thì số cạnh \[n\] là
A. \(9\).
B. \(10\).
C. \(7\).
D. \(8\).
Tổng số đo các góc trong của đa giác đều \[n\] cạnh là \(1440^\circ \) thì số cạnh \[n\] là
\(9\).
\(10\).
\(7\).
\(8\).
Tổng số đo các góc trong của đa giác đều \[n\] cạnh là \(1620^\circ \) thì số cạnh \[n\] là
\(9\).
\(10\).
\(11\).
\(8\).
Tổng số đo các góc trong của đa giác đều \[n\] cạnh là \(1620^\circ \) thì số cạnh \[n\] là
\(9\).
\(10\).
\(11\).
\(8\).
Tổng số đo các góc trong của đa giác đều \[n\] cạnh là \(1620^\circ \) thì số cạnh \[n\] là
\(9\).
\(10\).
\(11\).
\(8\).
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay thuận chiều \(120^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?
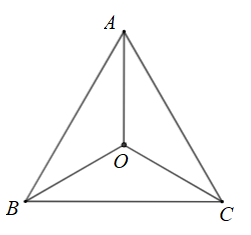
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[C\].
D. Điểm \[O\].
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay thuận chiều \(120^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?
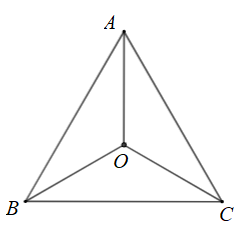
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[C\].
D. Điểm \[O\].
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay thuận chiều \(120^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?
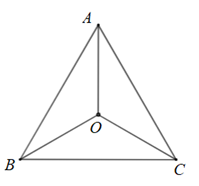
Điểm \[A\].
Điểm \[B\].
Điểm \[C\].
Điểm \[O\].
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay ngược chiều \(120^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?

A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm.
D. Điểm \[O\].
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay ngược chiều \(120^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?

A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm.
D. Điểm \[O\].
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay ngược chiều \(120^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?
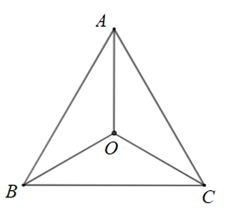
Điểm \[A\].
Điểm \[B\].
Điểm.
Điểm \[O\].
Cho hình vuông \(ABCD\)nội tiếp đường tròn tâm \[O\]. Phép quay ngược chiều \(180^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?
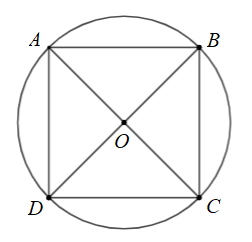
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[C\].
D. Điểm \[O\].
Cho hình vuông \(ABCD\)nội tiếp đường tròn tâm \[O\]. Phép quay ngược chiều \(180^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?
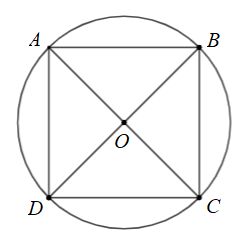
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[C\].
D. Điểm \[O\].
Cho hình vuông \(ABCD\)nội tiếp đường tròn tâm \[O\]. Phép quay ngược chiều \(180^\circ \) tâm \(O\) biến điểm \(A\) thành điểm nào?
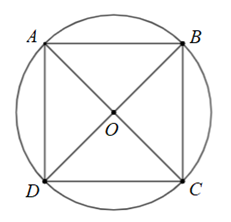
Điểm \[A\].
Điểm \[B\].
Điểm \[C\].
Điểm \[O\].
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay biến điểm \(A\) thành điểm \(B\) là phép quay nào?

A. phép quay thuận chiều \(90^\circ \)tâm \[O\].
B. phép quay thuận chiều \(120^\circ \) tâm \[O\].
C. phép thuận chiều \(180^\circ \)tâm \[O\].
D. phép ngược chiều \(90^\circ \)tâm \[O\].
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay biến điểm \(A\) thành điểm \(B\) là phép quay nào?

A. phép quay thuận chiều \(90^\circ \)tâm \[O\].
B. phép quay thuận chiều \(120^\circ \) tâm \[O\].
C. phép thuận chiều \(180^\circ \)tâm \[O\].
D. phép ngược chiều \(90^\circ \)tâm \[O\].
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay biến điểm \(A\) thành điểm \(B\) là phép quay nào?
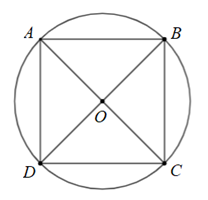
phép quay thuận chiều \(90^\circ \)tâm \[O\].
phép quay thuận chiều \(120^\circ \) tâm \[O\].
phép thuận chiều \(180^\circ \)tâm \[O\].
phép ngược chiều \(90^\circ \)tâm \[O\].
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \[90^\circ \] tâm \(O\) biến điểm \(B\) thành điểm nào?

A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[C\].
D. Điểm \[D\].
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \[90^\circ \] tâm \(O\) biến điểm \(B\) thành điểm nào?

A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[C\].
D. Điểm \[D\].
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \[90^\circ \] tâm \(O\) biến điểm \(B\) thành điểm nào?
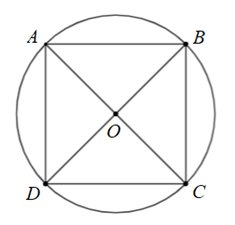
Điểm \[A\].
Điểm \[B\].
Điểm \[C\].
Điểm \[D\].
Cho ngũ giác đều \(ABCDE\) nội tiếp đường tròn\[\left( O \right)\]. Phép quay thuận chiều \[144^\circ \] tâm \(O\) biến điểm \(A\) thành điểm nào?
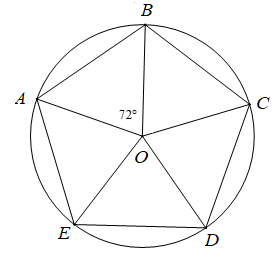
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[D\].
D. Điểm \[C\].
Cho ngũ giác đều \(ABCDE\) nội tiếp đường tròn\[\left( O \right)\]. Phép quay thuận chiều \[144^\circ \] tâm \(O\) biến điểm \(A\) thành điểm nào?
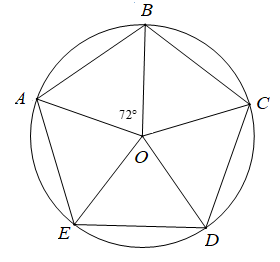
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[D\].
D. Điểm \[C\].
Cho ngũ giác đều \(ABCDE\) nội tiếp đường tròn\[\left( O \right)\]. Phép quay thuận chiều \[144^\circ \] tâm \(O\) biến điểm \(A\) thành điểm nào?
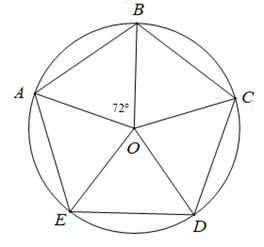
Điểm \[A\].
Điểm \[B\].
Điểm \[D\].
Điểm \[C\].
Cho tam giác đều \(ABC\)nội tiếp đường tròn tâm \[O\]. Phép quay giữ nguyên hình tam giác đều \(ABC\)là phép quay nào?

A. phép quay thuận chiều \(90^\circ \)tâm \[O\].
B. phép quay thuận chiều \(180^\circ \)tâm \[O\].
C. Phép ngược chiều \(90^\circ \)tâm \[O\].
D. phép thuận chiều \(120^\circ \) tâm \[O\].
Cho tam giác đều \(ABC\)nội tiếp đường tròn tâm \[O\]. Phép quay giữ nguyên hình tam giác đều \(ABC\)là phép quay nào?

A. phép quay thuận chiều \(90^\circ \)tâm \[O\].
B. phép quay thuận chiều \(180^\circ \)tâm \[O\].
C. Phép ngược chiều \(90^\circ \)tâm \[O\].
D. phép thuận chiều \(120^\circ \) tâm \[O\].
Cho tam giác đều \(ABC\)nội tiếp đường tròn tâm \[O\]. Phép quay giữ nguyên hình tam giác đều \(ABC\)là phép quay nào?
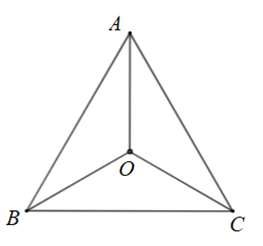
phép quay thuận chiều \(90^\circ \)tâm \[O\].
phép quay thuận chiều \(180^\circ \)tâm \[O\].
Phép ngược chiều \(90^\circ \)tâm \[O\].
phép thuận chiều \(120^\circ \) tâm \[O\].
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay giữ nguyên hình vuông
\(ABCD\) là phép quay nào?

A. Phép quay ngược chiều \(180^\circ \)tâm \(O\).
B. Phép quay thuận chiều \(120^\circ \)tâm \(O\).
C. Phép ngược chiều \(60^\circ \)tâm \(O\).
D. Phép ngược chiều \(100^\circ \)tâm \(O\).
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay giữ nguyên hình vuông
\(ABCD\) là phép quay nào?

A. Phép quay ngược chiều \(180^\circ \)tâm \(O\).
B. Phép quay thuận chiều \(120^\circ \)tâm \(O\).
C. Phép ngược chiều \(60^\circ \)tâm \(O\).
D. Phép ngược chiều \(100^\circ \)tâm \(O\).
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \[O\]. Phép quay giữ nguyên hình vuông \(ABCD\) là phép quay nào?
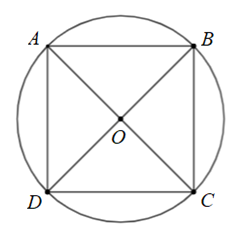
Phép quay ngược chiều \(180^\circ \)tâm \(O\).
Phép quay thuận chiều \(120^\circ \)tâm \(O\).
Phép ngược chiều \(60^\circ \)tâm \(O\).
Phép ngược chiều \(100^\circ \)tâm \(O\).
Cho hình vuông \(ABCD\), gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Phép quay thuận chiều \[180^\circ \] tâm \(O\) biến tam giác \(OAB\) thành tam giác nào?

A. \(\Delta OAB\).
B. \(\Delta OCB\).
C. \(\Delta OCD\).
D. \(\Delta ODA\).
Cho hình vuông \(ABCD\), gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Phép quay thuận chiều \[180^\circ \] tâm \(O\) biến tam giác \(OAB\) thành tam giác nào?

A. \(\Delta OAB\).
B. \(\Delta OCB\).
C. \(\Delta OCD\).
D. \(\Delta ODA\).
Cho hình vuông \(ABCD\), gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Phép quay thuận chiều \[180^\circ \] tâm \(O\) biến tam giác \(OAB\) thành tam giác nào?
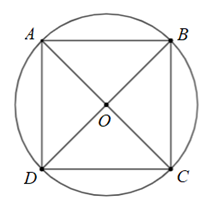
\(\Delta OAB\).
\(\Delta OCB\).
\(\Delta OCD\).
\(\Delta ODA\).
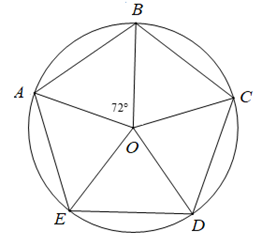
Cho ngũ giác đều \(ABCDE\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay thuận chiều \(72^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?

A. \(\Delta OBC\).
B. \(\Delta OCD\).
C. \(\Delta ODE\).
D. \(\Delta OEA\).
Cho ngũ giác đều \(ABCDE\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay thuận chiều \(72^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?

A. \(\Delta OBC\).
B. \(\Delta OCD\).
C. \(\Delta ODE\).
D. \(\Delta OEA\).
Cho ngũ giác đều \(ABCDE\) nội tiếp đường tròn tâm \[\left( O \right)\]. Phép quay thuận chiều \(72^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?
\(\Delta OBC\).
\(\Delta OCD\).
\(\Delta ODE\).
\(\Delta OEA\).
Cho bát giác đều \(ABCDEFGH\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \(135^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?
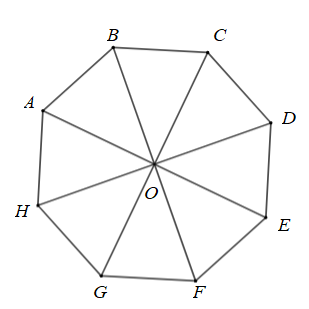
A. \(\Delta OBC\).\(\)
B. \(\Delta OCD\).
C. \(\Delta ODE\).
D. \(\Delta OEA\).
Cho bát giác đều \(ABCDEFGH\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \(135^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?
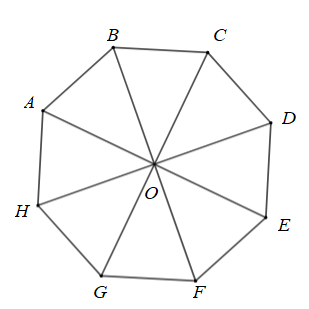
A. \(\Delta OBC\).\(\)
B. \(\Delta OCD\).
C. \(\Delta ODE\).
D. \(\Delta OEA\).
Cho bát giác đều \(ABCDEFGH\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \(135^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?
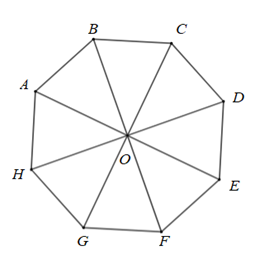
\(\Delta OBC\).
\(\Delta OCD\).
\(\Delta ODE\).
\(\Delta OEA\).
Phép quay tâm \(O\) (\(O\) là một điểm bất kì) với góc quay bằng bao nhiêu biến \(\Delta ABC\) cân
thành chính nó?
A. \(0^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(90^\circ \).
Phép quay tâm \(O\) (\(O\) là một điểm bất kì) với góc quay bằng bao nhiêu biến \(\Delta ABC\) cân
thành chính nó?
A. \(0^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(90^\circ \).
Phép quay tâm \(O\) (\(O\) là một điểm bất kì) với góc quay bằng bao nhiêu biến \(\Delta ABC\) cân thành chính nó?
\(0^\circ \).
\(45^\circ \).
\(60^\circ \).
\(90^\circ \).
Phép quay tâm \(O\) (\(O\) là tâm tam giác đều \(MNP\)) với góc quay bằng bao nhiêu biến
\(\Delta MNP\)đều thành chính nó?
A. \(270^\circ \).
B. \(240^\circ \).
C. \(90^\circ \).
D. \(45^\circ \).
Phép quay tâm \(O\) (\(O\) là tâm tam giác đều \(MNP\)) với góc quay bằng bao nhiêu biến
\(\Delta MNP\)đều thành chính nó?
A. \(270^\circ \).
B. \(240^\circ \).
C. \(90^\circ \).
D. \(45^\circ \).
Phép quay tâm \(O\) (\(O\) là tâm tam giác đều \(MNP\)) với góc quay bằng bao nhiêu biến \(\Delta MNP\)đều thành chính nó?
\(270^\circ \).
\(240^\circ \).
\(90^\circ \).
\(45^\circ \)
Phép quay tâm\(O\) (\(O\) là tâm hình vuông \(ABCD\)) với góc quay bằng bao nhiêu biến
hình vuông \(ABCD\) thành chính nó?
A. \(240^\circ \).
B. \(120^\circ \).
C. \(90^\circ \).
D. \(45^\circ \).
Phép quay tâm\(O\) (\(O\) là tâm hình vuông \(ABCD\)) với góc quay bằng bao nhiêu biến
hình vuông \(ABCD\) thành chính nó?
A. \(240^\circ \).
B. \(120^\circ \).
C. \(90^\circ \).
D. \(45^\circ \).
Phép quay tâm\(O\) (\(O\) là tâm hình vuông \(ABCD\)) với góc quay bằng bao nhiêu biến hình vuông \(ABCD\) thành chính nó?
\(240^\circ \).
\(120^\circ \).
\(90^\circ \).
\(45^\circ \).
Phép quay tâm\(O\) (\(O\) là tâm hình chữ nhật \(ABCD\)) với góc quay bằng bao nhiêu biến hình chữ nhật\(ABCD\) thành chính nó?
A. \(45^\circ \).
B. \(90^\circ \).
C. \(120^\circ \).
D. \(360^\circ \).
Phép quay tâm\(O\) (\(O\) là tâm hình chữ nhật \(ABCD\)) với góc quay bằng bao nhiêu biến hình chữ nhật\(ABCD\) thành chính nó?
A. \(45^\circ \).
B. \(90^\circ \).
C. \(120^\circ \).
D. \(360^\circ \).
Phép quay tâm \(O\) (\(O\) là tâm hình chữ nhật \(ABCD\)) với góc quay bằng bao nhiêu biến hìnhchữnhật \(ABCD\) thành chính nó?
\(45^\circ \).
\(90^\circ \).
\(120^\circ \).
\(360^\circ \).
Phép quay tâm\(O\) (\(O\) là tâm hình ngũ giác đều) với góc quay bằng bao nhiêu biến hình
ngũ giác đều thành chính nó?
A. \(144^\circ \).
B. \(100^\circ \).
C. \(90^\circ \).
D. \(60^\circ \).
Phép quay tâm\(O\) (\(O\) là tâm hình ngũ giác đều) với góc quay bằng bao nhiêu biến hình
ngũ giác đều thành chính nó?
A. \(144^\circ \).
B. \(100^\circ \).
C. \(90^\circ \).
D. \(60^\circ \).
Phép quay tâm\(O\) (\(O\) là tâm hình ngũ giác đều) với góc quay bằng bao nhiêu biến hình ngũ giác đều thành chính nó?
\(144^\circ \).
\(100^\circ \).
\(90^\circ \).
\(60^\circ \).
Cho \(\Delta MNP\) vuông cân tại \(M\) có \(O\) là trung điểm của cạnh \(NP\).
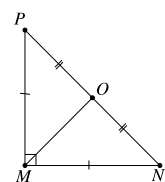
Khẳng định nào sau đây sai?
A. Phép quay thuận chiều \(90^\circ \) tâm \(M\) biến điểm \(P\) thành điểm \(N\).
B. Phép quay ngược chiều \(90^\circ \) tâm \(O\) biến điểm \(P\) thành điểm \(M\).
C. Phép quay ngược chiều \(90^\circ \) tâm \(O\) biến điểm \(M\) thành điểm \(N\).
D. Phép quay thuận chiều \(45^\circ \) tâm \(M\) biến điểm \(O\) thành điểm \(N\).
Cho \(\Delta MNP\) vuông cân tại \(M\) có \(O\) là trung điểm của cạnh \(NP\).
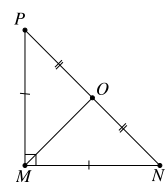
Khẳng định nào sau đây sai?
A. Phép quay thuận chiều \(90^\circ \) tâm \(M\) biến điểm \(P\) thành điểm \(N\).
B. Phép quay ngược chiều \(90^\circ \) tâm \(O\) biến điểm \(P\) thành điểm \(M\).
C. Phép quay ngược chiều \(90^\circ \) tâm \(O\) biến điểm \(M\) thành điểm \(N\).
D. Phép quay thuận chiều \(45^\circ \) tâm \(M\) biến điểm \(O\) thành điểm \(N\).
Cho \(\Delta MNP\) vuông cân tại \(M\) có \(O\) là trung điểm của cạnh \(NP\).
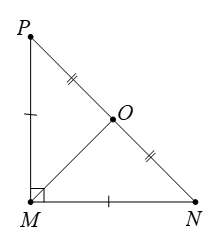
Khẳng định nào sau đây sai?
Phép quay thuận chiều \(90^\circ \) tâm \(M\) biến điểm \(P\) thành điểm \(N\).
Phép quay ngược chiều \(90^\circ \) tâm \(O\) biến điểm \(P\) thành điểm \(M\).
Phép quay ngược chiều \(90^\circ \) tâm \(O\) biến điểm \(M\) thành điểm \(N\).
Phép quay thuận chiều \(45^\circ \) tâm \(M\) biến điểm \(O\) thành điểm \(N\).
Cho tam giác đều \[ABC\]có \[G\] là trọng tâm. Phép quay tâm \[G\] với góc quay nào dưới
đây biến tam giác \[ABC\]thành chính nó.
A. \(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(120^\circ \).
Cho tam giác đều \[ABC\]có \[G\] là trọng tâm. Phép quay tâm \[G\] với góc quay nào dưới
đây biến tam giác \[ABC\]thành chính nó.
A. \(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(120^\circ \).
Cho tam giác đều \[ABC\]có \[G\] là trọng tâm. Phép quay tâm \[G\] với góc quay nào dưới đây biến tam giác \[ABC\]thành chính nó.
\(30^\circ \).
\(45^\circ \).
\(60^\circ \).
\(120^\circ \).
Cho hình vuông \(MNPQ\) tâm \(O\). Phép quay giữ nguyên hình vuông \(MNPQ\) là
A. Phép quay thuận chiều \(45^\circ \) tâm \(O\).
B. Phép quay thuận chiều \(270^\circ \) tâm \(O\).
C. Phép quay ngược chiều \(90^\circ \) tâm \(M\).
D. Phép quay ngược chiều \(180^\circ \) tâm \(M\).
Cho hình vuông \(MNPQ\) tâm \(O\). Phép quay giữ nguyên hình vuông \(MNPQ\) là
A. Phép quay thuận chiều \(45^\circ \) tâm \(O\).
B. Phép quay thuận chiều \(270^\circ \) tâm \(O\).
C. Phép quay ngược chiều \(90^\circ \) tâm \(M\).
D. Phép quay ngược chiều \(180^\circ \) tâm \(M\).
Cho hình vuông \(MNPQ\) tâm \(O\). Phép quay giữ nguyên hình vuông \(MNPQ\) là
Phép quay thuận chiều \(45^\circ \) tâm \(O\).
Phép quay thuận chiều \(270^\circ \) tâm \(O\).
Phép quay ngược chiều \(90^\circ \) tâm \(M\).
Phép quay ngược chiều \(180^\circ \) tâm \(M\).
Đường viền ngoài của chiếc đồng hồ trong hình dưới đây được làm theo hình bát giác đều, gọi \(O\) là tâm của hình bát giác đều này. Các phép quay biến đa giác này thành chính nó là

Các phép quay \(45^\circ \), \[180^\circ \], \[315^\circ \], \[360^\circ \] tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
B. Các phép quay \(45^\circ \), \(90^\circ \), \(240^\circ \), \[270^\circ \]tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
C. Các phép quay \(45^\circ \), \(120^\circ \), \(180^\circ \), \(270^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
D. Các phép quay \(90^\circ \), \(150^\circ \), \(180^\circ \), \[360^\circ \] tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Đường viền ngoài của chiếc đồng hồ trong hình dưới đây được làm theo hình bát giác đều, gọi \(O\) là tâm của hình bát giác đều này. Các phép quay biến đa giác này thành chính nó là

Các phép quay \(45^\circ \), \[180^\circ \], \[315^\circ \], \[360^\circ \] tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
B. Các phép quay \(45^\circ \), \(90^\circ \), \(240^\circ \), \[270^\circ \]tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
C. Các phép quay \(45^\circ \), \(120^\circ \), \(180^\circ \), \(270^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
D. Các phép quay \(90^\circ \), \(150^\circ \), \(180^\circ \), \[360^\circ \] tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Đường viền ngoài của chiếc đồng hồ trong hình dưới đây được làm theo hình bát giác đều, gọi \(O\) là tâm của hình bát giác đều này. Các phép quay biến đa giác này thành chính nó là

Các phép quay \(45^\circ \), \[180^\circ \], \[315^\circ \], \[360^\circ \] tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Các phép quay \(45^\circ \), \(90^\circ \), \(240^\circ \), \[270^\circ \]tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Các phép quay \(45^\circ \), \(120^\circ \), \(180^\circ \), \(270^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Các phép quay \(90^\circ \), \(150^\circ \), \(180^\circ \), \[360^\circ \] tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Đường viền ngoài của biển báo giao thông trong hình dưới đây được làm theo hình tam giác đều, gọi \(O\) là tâm của đường tròn ngoại tiếp tam giác đều này. Các phép quay biến hình tam giác đều này thành chính nó là

A. Các phép quay \(60^\circ \), \(120^\circ \), \(180^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
B. Các phép quay \(120^\circ \), \(240^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
C. Các phép quay \(120^\circ \), \(180^\circ \), \(200^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
D. Các phép quay \(90^\circ \), \(180^\circ \), \(240^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Đường viền ngoài của biển báo giao thông trong hình dưới đây được làm theo hình tam giác đều, gọi \(O\) là tâm của đường tròn ngoại tiếp tam giác đều này. Các phép quay biến hình tam giác đều này thành chính nó là

A. Các phép quay \(60^\circ \), \(120^\circ \), \(180^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
B. Các phép quay \(120^\circ \), \(240^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
C. Các phép quay \(120^\circ \), \(180^\circ \), \(200^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
D. Các phép quay \(90^\circ \), \(180^\circ \), \(240^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Đường viền ngoài của biển báo giao thông trong hình dưới đây được làm theo hình tam giác đều, gọi \(O\) là tâm của đường tròn ngoại tiếp tam giác đều này. Các phép quay biến hình tam giác đều này thành chính nó là

Các phép quay \(60^\circ \), \(120^\circ \), \(180^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Các phép quay \(120^\circ \), \(240^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Các phép quay \(120^\circ \), \(180^\circ \), \(200^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Các phép quay \(90^\circ \), \(180^\circ \), \(240^\circ \), \(360^\circ \) tâm \(O\) cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
