109 câu hỏi
Chọn khẳng định sai trong các phát biểu sau?
Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn.
Mỗi hình chữ nhật là một tứ giác nội tiếp đường tròn.
Tứ giác có bốn cạnh tiếp xúc với đường tròn được gọi là tứ giác nội tiếp đường tròn.
Mỗi hình vuông là một tứ giác nội tiếp đường tròn.
Chọn khẳng định sai trong các phát biểu sau?
A. Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn.
B. Mỗi hình chữ nhật là một tứ giác nội tiếp đường tròn.
C. Tứ giác có bốn cạnh tiếp xúc với đường tròn được gọi là tứ giác nội tiếp đường tròn.
D. Mỗi hình vuông là một tứ giác nội tiếp đường tròn.
Lời giải
Chọn C
Câu 2:Cho các hình: hình vuông, hình chữ nhật, hình bình hành, hình thoi. Trong các hình nói trên có bao nhiêu hình không là tứ giác nội tiếp?
A. \[1\]
B. \[2.\]
C. \[3\].
D. \[4\].
Chọn khẳng định sai trong các phát biểu sau?
A. Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn.
B. Mỗi hình chữ nhật là một tứ giác nội tiếp đường tròn.
C. Tứ giác có bốn cạnh tiếp xúc với đường tròn được gọi là tứ giác nội tiếp đường tròn.
D. Mỗi hình vuông là một tứ giác nội tiếp đường tròn.
Lời giải
Chọn C
Câu 2: Cho các hình: hình vuông, hình chữ nhật, hình bình hành, hình thoi. Trong các hình nói trên có bao nhiêu hình không là tứ giác nội tiếp?
A. \[1\]
B. \[2.\]
C. \[3\].
D. \[4\].
Cho các hình: hình vuông, hình chữ nhật, hình bình hành, hình thoi. Trong các hình nói trên có bao nhiêu hình không là tứ giác nội tiếp?
\[1\]
\[2.\]
\[3\].
\[4\].
Trong một tứ giác nội tiếp, tổng số đo của hai góc đối nhau bằng

A. \(180^\circ \)
B. \(90^\circ \)
C. \(360^\circ \)
D. \(120^\circ \)
Lời giải
Chọn A
Câu 5:Có bao nhiêu tứ giác nội tiếp đường tròn trong các hình vẽ dưới đây?
A. \[1\]
B. \[2.\]
C. \[3\].
D. \[4\].
Trong một tứ giác nội tiếp, tổng số đo của hai góc đối nhau bằng

A. \(180^\circ \)
B. \(90^\circ \)
C. \(360^\circ \)
D. \(120^\circ \)
Lời giải
Chọn A
Câu 5: Có bao nhiêu tứ giác nội tiếp đường tròn trong các hình vẽ dưới đây?
A. \[1\]
B. \[2.\]
C. \[3\].
D. \[4\].
Cho các hình: Hình vuông, hình chữ nhật, hình bình hành, hình thang vuông, hình thang cân, hình thoi. Trong các hình nói trên có bao nhiêu hình là tứ giác nội tiếp trong một đường tròn?
\[1\]
\[2.\]
\[3\].
\[4\].
Có bao nhiêu tứ giác không nội tiếp đường tròn trong các hình vẽ dưới đây?

A. \[1\]
B. \[2.\]
C. \[3\].
D. \[4\].
Có bao nhiêu tứ giác không nội tiếp đường tròn trong các hình vẽ dưới đây?

A. \[1\]
B. \[2.\]
C. \[3\].
D. \[4\].
Trong một tứ giác nội tiếp, tổng số đo của hai góc đối nhau bằng
\(180^\circ \)
\(90^\circ \)
\(360^\circ \)
\(120^\circ \)
Tứ giác nào sau đây không nội tiếp được đường tròn?

Tứ giác \[ABCD\]
Tứ giác \[MNPQ\]
Tứ giác \[QRST\]
Tứ giác \[EFGH\]
Lời giải
Chọn C
Câu 8:Cho hình vẽ bên, số tứ giác nội tiếp được trong đường tròn là
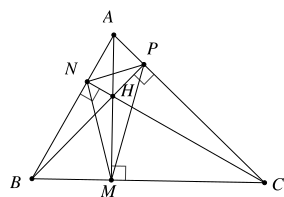
Có \(3\) hình tứ giác nội tiếp
Có \(4\) hình tứ giác nội tiếp
C. Có \(5\) hình tứ giác nội tiếp
D. Có \(6\) hình tứ giác nội tiếp
Tứ giác nào sau đây không nội tiếp được đường tròn?

Tứ giác \[ABCD\]
Tứ giác \[MNPQ\]
Tứ giác \[QRST\]
Tứ giác \[EFGH\]
Lời giải
Chọn C
C.
Câu 8: Cho hình vẽ bên, số tứ giác nội tiếp được trong đường tròn là
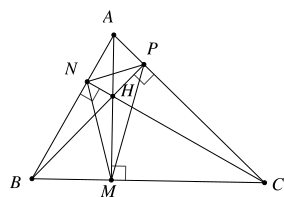
Có \(3\) hình tứ giác nội tiếp
Có \(4\) hình tứ giác nội tiếp
C. Có \(5\) hình tứ giác nội tiếp
D. Có \(6\) hình tứ giác nội tiếp
Có bao nhiêu tứ giác nội tiếp đường tròn trong các hình vẽ dưới đây?

\[1\]
\[2.\]
\[3\].
\[4\].
Cho hình vẽ sau. Chọn khẳng định sai trong các phát biểu sau?
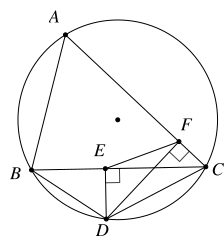
Tứ giác \(ABDC\)nội tiếp được đường tròn.
Tứ giác \(DEFC\)nội tiếp được đường tròn
\(\widehat {DEF} + \widehat {FCD} = 180^\circ \).
Tứ giác \(DEFC\) không nội tiếp được đường tròn.
Cho hình vẽ sau. Chọn khẳng định sai trong các phát biểu sau?
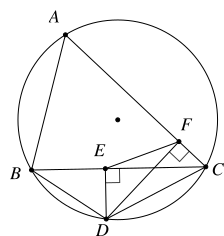
Tứ giác \(ABDC\)nội tiếp được đường tròn.
Tứ giác \(DEFC\)nội tiếp được đường tròn
\(\widehat {DEF} + \widehat {FCD} = 180^\circ \).
Tứ giác \(DEFC\) không nội tiếp được đường tròn.
Có bao nhiêu tứ giác không nội tiếp đường tròn trong các hình vẽ dưới đây?

\[1\]
\[2.\]
\[3\].
\[4\].
Cho điểm \(A\) nằm ngoài \(\left( O \right)\), qua \(A\) vẽ hai tiếp tuyến \(AB,\)\(AC\) với \(B,\)\(C\) là tiếp điểm.
Chọn khẳng định đúng.

A. Tứ giác \(ABOC\)là hình thoi.
B. Tứ giác \(ABOC\)không nội tiếp được đường tròn.
C. Tứ giác \(ABOC\)là hình bình hành.
D. Tứ giác \(ABOC\)nội tiếp được đường tròn.
Cho điểm \(A\) nằm ngoài \(\left( O \right)\), qua \(A\) vẽ hai tiếp tuyến \(AB,\)\(AC\) với \(B,\)\(C\) là tiếp điểm.
Chọn khẳng định đúng.

A. Tứ giác \(ABOC\)là hình thoi.
B. Tứ giác \(ABOC\)không nội tiếp được đường tròn.
C. Tứ giác \(ABOC\)là hình bình hành.
D. Tứ giác \(ABOC\)nội tiếp được đường tròn.
Tứ giác nào sau đây không nội tiếp được đường tròn?

Tứ giác \[ABCD\]
Tứ giác \[MNPQ\]
Tứ giác \[QRST\]
Tứ giác \[EFGH\]
Cho tứ giác \(ABCD\) nội tiếp đường tròn biết \[\widehat A = 2\widehat C\]. Vậy số đo\[\widehat C\, & \]bằng:
A. \(60^\circ \)
B. \(120^\circ \)
C. \(50^\circ \)
D. \(100^\circ \)
Cho tứ giác \(ABCD\) nội tiếp đường tròn biết \[\widehat A = 2\widehat C\]. Vậy số đo\[\widehat C\, & \]bằng:
A. \(60^\circ \)
B. \(120^\circ \)
C. \(50^\circ \)
D. \(100^\circ \)
Cho hình vẽ bên, số tứ giác nội tiếp được trong đường tròn là

Có \(3\) hình tứ giác nội tiếp
Có \(4\) hình tứ giác nội tiếp
Có \(5\) hình tứ giác nội tiếp
Có \(6\) hình tứ giác nội tiếp
Cho tứ giác \(MNPQ\) nội tiếp đường tròn với\[\widehat {MQP} - \widehat {MNP} = 10^\circ \]. Số đo \[\widehat {MQP}\] bằng:
A. \[100^\circ \]
B. \[95^\circ \]
C. \[80^\circ \]
D. \[90^\circ \]
Cho tứ giác \(MNPQ\) nội tiếp đường tròn với\[\widehat {MQP} - \widehat {MNP} = 10^\circ \]. Số đo \[\widehat {MQP}\] bằng:
A. \[100^\circ \]
B. \[95^\circ \]
C. \[80^\circ \]
D. \[90^\circ \]
Cho hình vẽ sau. Chọn khẳng định sai trong các phát biểu sau?

Tứ giác \(ABDC\)nội tiếp được đường tròn.
Tứ giác \(DEFC\)nội tiếp được đường tròn
\(\widehat {DEF} + \widehat {FCD} = 180^\circ \).
Tứ giác \(DEFC\) không nội tiếp được đường tròn.
Cho tứ giác \(ABCD\) nội tiếp đường tròn, biết \[\widehat A = 100^\circ ,\,\,\widehat B = 70^\circ \]. Vậy số đo\[\widehat C\, & ;\,\,\widehat D\,\]bằng:
A. \[\widehat C = 80^\circ ;\,\,\widehat D = 100^\circ \]
B. \[\widehat C = 80^\circ ;\,\,\widehat D = 70^\circ \]
C. \[\widehat C = 80^\circ ;\,\,\widehat D = 140^\circ \]
D. \[\widehat C = 80^\circ ;\,\,\widehat D = 110^\circ \]
Cho tứ giác \(ABCD\) nội tiếp đường tròn, biết \[\widehat A = 100^\circ ,\,\,\widehat B = 70^\circ \]. Vậy số đo\[\widehat C\, & ;\,\,\widehat D\,\]bằng:
A. \[\widehat C = 80^\circ ;\,\,\widehat D = 100^\circ \]
B. \[\widehat C = 80^\circ ;\,\,\widehat D = 70^\circ \]
C. \[\widehat C = 80^\circ ;\,\,\widehat D = 140^\circ \]
D. \[\widehat C = 80^\circ ;\,\,\widehat D = 110^\circ \]
Cho hình vẽ sau: Khi đó \[\widehat {BCD}\] bằng:
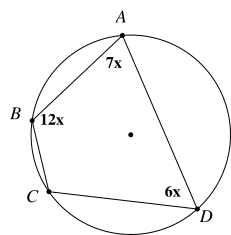
A. \[120^\circ \]
B. \[60^\circ \]
C. \[70^\circ \]
D. \[110^\circ \]
Cho điểm \(A\) nằm ngoài \(\left( O \right)\), qua \(A\) vẽ hai tiếp tuyến \(AB,\)\(AC\) với \(B,\)\(C\) là tiếp điểm.
Chọn khẳng định đúng.

Tứ giác \(ABOC\)là hình thoi.
Tứ giác \(ABOC\)không nội tiếp được đường tròn.
Tứ giác \(ABOC\)là hình bình hành.
Tứ giác \(ABOC\)nội tiếp được đường tròn.
Cho hình vẽ sau: Khi đó \[\widehat {BCD}\] bằng:
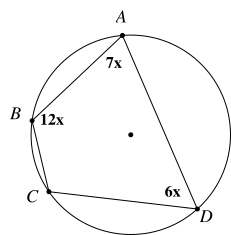
A. \[120^\circ \]
B. \[60^\circ \]
C. \[70^\circ \]
D. \[110^\circ \]
Cho tứ giác \(MNPQ\) nội tiếp đường tròn \((O)\)và \(\widehat {NPQ} = 100^\circ \), số đo \(\widehat {NOQ}\)bằng
A. \(80^\circ \)
B. \(160^\circ \)
C. \(240^\circ \)
D. \(140^\circ \)
Cho tứ giác \(ABCD\) nội tiếp đường tròn biết \[\widehat A = 2\widehat C\]. Vậy số đo \[\widehat C\] bằng:
\(60^\circ \)
\(120^\circ \)
\(50^\circ \)
\(100^\circ \)
Cho tứ giác \(MNPQ\) nội tiếp đường tròn \((O)\)và \(\widehat {NPQ} = 100^\circ \), số đo \(\widehat {NOQ}\)bằng
A. \(80^\circ \)
B. \(160^\circ \)
C. \(240^\circ \)
D. \(140^\circ \)
Cho tam giác \(ABC\) vuông tại \(A\) và lấy điểm \(E\) bất kì trên cạnh \(AB\). Qua \(B\) vẽ một đường thẳng vuông góc với \(CE\) tại \(D\) và cắt tia \(CA\) tại \(H\), biết \(\widehat {ACB} = 34^\circ \), số đo \(\widehat {ADH}\) bằng
A. \(38^\circ \)
B. \(40^\circ \)
C. \(34^\circ \)
D. \(36^\circ \)
Cho tứ giác \(MNPQ\) nội tiếp đường tròn với\[\widehat {MQP} - \widehat {MNP} = 10^\circ \]. Số đo \[\widehat {MQP}\] bằng:
\[100^\circ \]
\[95^\circ \]
\[80^\circ \]
\[90^\circ \]
Cho tam giác \(ABC\) vuông tại \(A\) và lấy điểm \(E\) bất kì trên cạnh \(AB\). Qua \(B\) vẽ một đường thẳng vuông góc với \(CE\) tại \(D\) và cắt tia \(CA\) tại \(H\), biết \(\widehat {ACB} = 34^\circ \), số đo \(\widehat {ADH}\) bằng
A. \(38^\circ \)
B. \(40^\circ \)
C. \(34^\circ \)
D. \(36^\circ \)
Cho tam giác \(ABC\) có \(CK\) và \(BD\) là hai đường cao, biết \(\widehat {ACB} = 50^\circ \). Số đo\(\widehat {AKD}\) bằng
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(70^\circ \)
Cho tứ giác \(ABCD\) nội tiếp đường tròn, biết \[\widehat A = 100^\circ ,\,\,\widehat B = 70^\circ \]. Vậy số đo\[\widehat C\] & \[\widehat D\] bằng:
\[\widehat C = 80^\circ ;\,\,\widehat D = 100^\circ \]
\[\widehat C = 80^\circ ;\,\,\widehat D = 70^\circ \]
\[\widehat C = 80^\circ ;\,\,\widehat D = 140^\circ \]
\[\widehat C = 80^\circ ;\,\,\widehat D = 110^\circ \]
Cho tam giác \(ABC\) có \(CK\) và \(BD\) là hai đường cao, biết \(\widehat {ACB} = 50^\circ \). Số đo\(\widehat {AKD}\) bằng
A. \(40^\circ \)
B. \(50^\circ \)
C. \(60^\circ \)
D. \(70^\circ \)
Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O),\) hai đường thẳng \(AB,\) \(CD\) cắt nhau tại \(M\) và hai đường thẳng \(AD,\) \(BC\) cắt nhau tại \(N\) như hình vẽ. Biết các góc \(\widehat {ANB} = a^\circ ;\)\(\widehat {AMD} = b^\circ \).
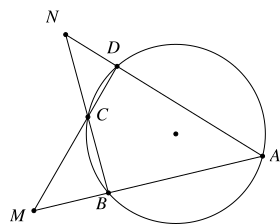
Số đo góc \(\widehat {BAD}\) bằng
A. \(90^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
B. \(180^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
C. \(90^\circ + \frac{{a^\circ + b^\circ }}{2}.\)
D. \(90^\circ - \left( {a^\circ + b^\circ } \right).\)
Cho hình vẽ sau: Khi đó \[\widehat {BCD}\] bằng:
![Cho hình vẽ sau: Khi đó \[\widehat {BCD}\] bằng: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid7-1755532480.png)
\[120^\circ \]
\[60^\circ \]
\[70^\circ \]
\[110^\circ \]
Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O),\) hai đường thẳng \(AB,\) \(CD\) cắt nhau tại \(M\) và hai đường thẳng \(AD,\) \(BC\) cắt nhau tại \(N\) như hình vẽ. Biết các góc \(\widehat {ANB} = a^\circ ;\)\(\widehat {AMD} = b^\circ \).
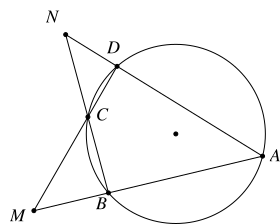
Số đo góc \(\widehat {BAD}\) bằng
A. \(90^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
B. \(180^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
C. \(90^\circ + \frac{{a^\circ + b^\circ }}{2}.\)
D. \(90^\circ - \left( {a^\circ + b^\circ } \right).\)
Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O),\) hai đường thẳng \(AB,\) \(CD\) cắt nhau tại \(M\) và hai đường thẳng \(AD,\) \(BC\) cắt nhau tại \(N\) như hình vẽ. Biết các góc \(\widehat {ANB} = a^\circ ;\)\(\widehat {AMD} = b^\circ \).

Số đo góc \(\widehat {BCD}\) bằng
A. \(90^\circ + \frac{{a^\circ + b^\circ }}{2}.\)
B. \(180^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
C. \(90^\circ + a^\circ + b^\circ .\)
D. \(180^\circ - \left( {a^\circ + b^\circ } \right).\)
Cho tứ giác \(MNPQ\) nội tiếp đường tròn \((O)\)và \(\widehat {NPQ} = 100^\circ \), số đo \(\widehat {NOQ}\)bằng
\(80^\circ \)
\(160^\circ \)
\(240^\circ \)
\(140^\circ \)
Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O),\) hai đường thẳng \(AB,\) \(CD\) cắt nhau tại \(M\) và hai đường thẳng \(AD,\) \(BC\) cắt nhau tại \(N\) như hình vẽ. Biết các góc \(\widehat {ANB} = a^\circ ;\)\(\widehat {AMD} = b^\circ \).

Số đo góc \(\widehat {BCD}\) bằng
A. \(90^\circ + \frac{{a^\circ + b^\circ }}{2}.\)
B. \(180^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
C. \(90^\circ + a^\circ + b^\circ .\)
D. \(180^\circ - \left( {a^\circ + b^\circ } \right).\)
Cho tứ giác \[ABCD\]nội tiếp đường tròn \[\left( {O\,;\,R} \right)\]có \[AB = BC = R\]. Số đo \[\widehat {ABC}\] là:
A. \[120^\circ \]
B. \[140^\circ \]
C. \[70^\circ \]
D. \[60^\circ \]
Cho tam giác \(ABC\) vuông tại \(A\) và lấy điểm \(E\) bất kì trên cạnh \(AB\). Qua \(B\) vẽ một đường thẳng vuông góc với \(CE\) tại \(D\) và cắt tia \(CA\) tại \(H\), biết \(\widehat {ACB} = 34^\circ \), số đo \(\widehat {ADH}\) bằng
\(38^\circ \)
\(40^\circ \)
\(34^\circ \)
\(36^\circ \)
Cho tứ giác \[ABCD\]nội tiếp đường tròn \[\left( {O\,;\,R} \right)\]có \[AB = BC = R\]. Số đo \[\widehat {ABC}\] là:
A. \[120^\circ \]
B. \[140^\circ \]
C. \[70^\circ \]
D. \[60^\circ \]
Cho tứ giác\[ABCD\] nội tiếp được đường tròn. Biết \(\widehat {C\,} = 60^\circ ,{\rm{ }}\widehat {\rm{D}} = 80^\circ \). Khi đó:
\(\widehat {A\,\,} = 60^\circ ;{\rm{ }}\widehat {B\,} = 80^\circ \)
\(\widehat {A\,\,} = 120^\circ ;{\rm{ }}\widehat {\rm{B}} = 100^\circ \)
\(\widehat A = 120^\circ ;{\rm{ }}\widehat {\rm{B}} = 130^\circ \)
\(\widehat A = 90^\circ ;{\rm{ }}\widehat B = 100^\circ \)
Cho tam giác \(ABC\) có \(CK\) và \(BD\) là hai đường cao, biết \(\widehat {ACB} = 50^\circ \). Số đo\(\widehat {AKD}\) bằng
\(40^\circ \)
\(50^\circ \)
\(60^\circ \)
\(70^\circ \)
Cho tứ giác\[ABCD\] nội tiếp được đường tròn. Biết \(\widehat {C\,} = 60^\circ ,{\rm{ }}\widehat {\rm{D}} = 80^\circ \). Khi đó:
\(\widehat {A\,\,} = 60^\circ ;{\rm{ }}\widehat {B\,} = 80^\circ \)
\(\widehat {A\,\,} = 120^\circ ;{\rm{ }}\widehat {\rm{B}} = 100^\circ \)
\(\widehat A = 120^\circ ;{\rm{ }}\widehat {\rm{B}} = 130^\circ \)
\(\widehat A = 90^\circ ;{\rm{ }}\widehat B = 100^\circ \)
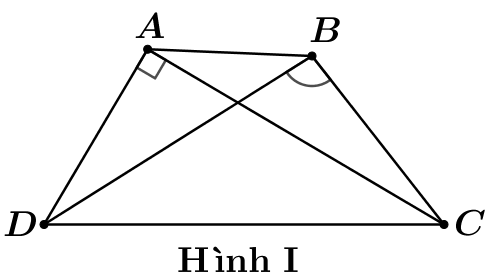
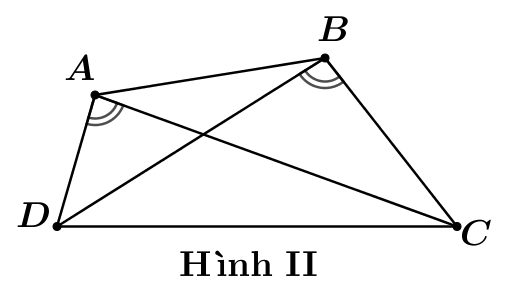
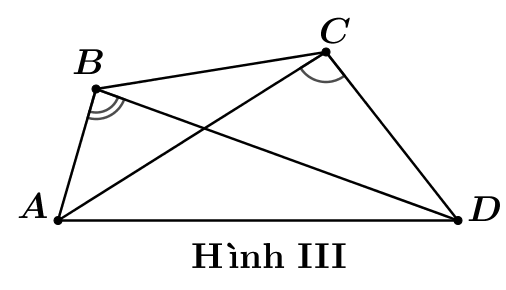
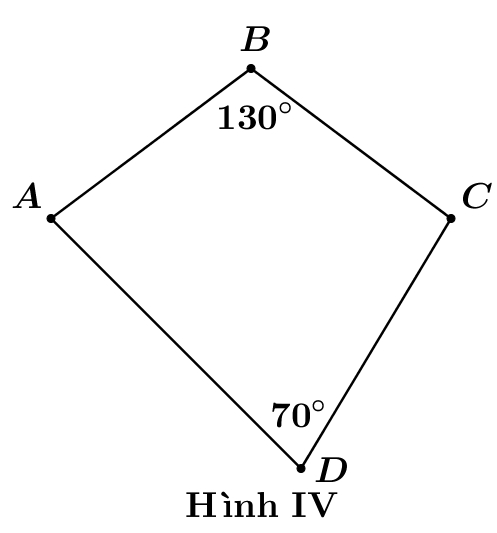
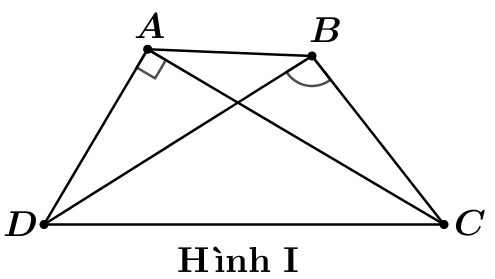
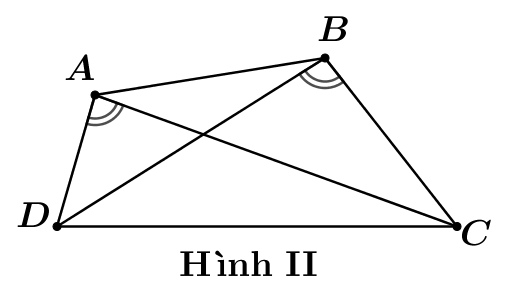
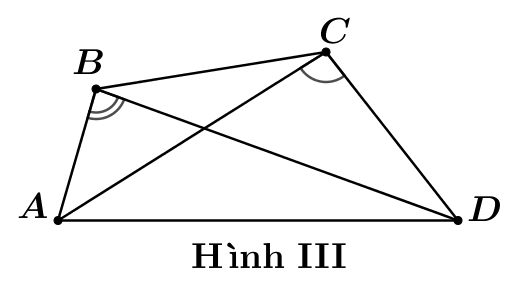
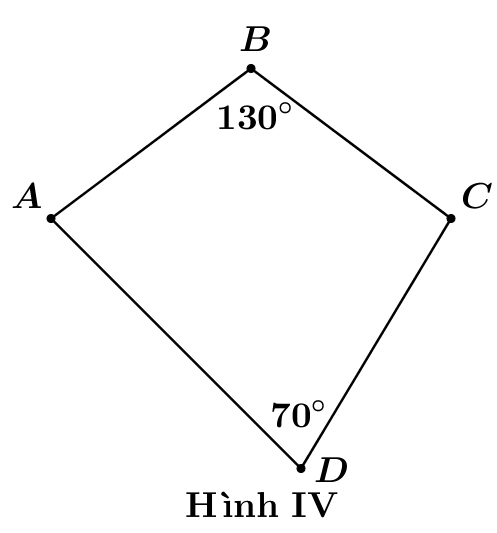
Trong các hình vẽ tứ giác\[ABCD\]sau hãy chọn hình vẽ có tứ giác nội tiếp trong đường tròn.
|
|
|
|
Hình I
Hình II
Hình III
Hình IV
Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O),\) hai đường thẳng \(AB,\) \(CD\) cắt nhau tại \(M\) và hai đường thẳng \(AD,\) \(BC\) cắt nhau tại \(N\) như hình vẽ. Biết các góc \(\widehat {ANB} = a^\circ ;\)\(\widehat {AMD} = b^\circ \).
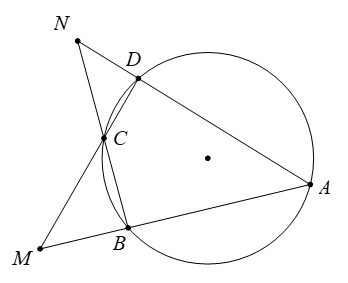
Số đo góc \(\widehat {BAD}\) bằng
\(90^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
\(180^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
\(90^\circ + \frac{{a^\circ + b^\circ }}{2}.\)
\(90^\circ - \left( {a^\circ + b^\circ } \right).\)
Trong các hình vẽ tứ giác\[ABCD\]sau hãy chọn hình vẽ có tứ giác nội tiếp trong đường tròn.
|
|
|
|
Hình I
Hình II
Hình III
Hình IV
Trong các phát biểu sau, phát biểu nào là đúng
Mọi tứ giác đều nội tiếp được đường tròn.
Trong một tứ giác nội tiếp, tổng số đo hai góc đối bằng \(90^\circ \).
Tứ giác có tổng hai góc bằng \(180^\circ \) thì tứ giác đó nội tiếp.
Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới hai góc bằng nhau thì tứ giác đó nội tiếp.
Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O),\) hai đường thẳng \(AB,\) \(CD\) cắt nhau tại \(M\) và hai đường thẳng \(AD,\) \(BC\) cắt nhau tại \(N\) như hình vẽ. Biết các góc \(\widehat {ANB} = a^\circ ;\)\(\widehat {AMD} = b^\circ \).
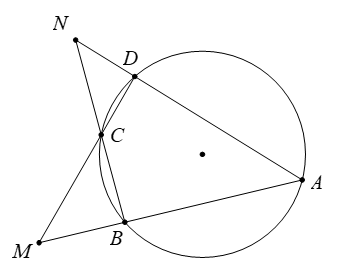
Số đo góc \(\widehat {BCD}\) bằng
\(90^\circ + \frac{{a^\circ + b^\circ }}{2}.\)
\(180^\circ - \frac{{a^\circ + b^\circ }}{2}.\)
\(90^\circ + a^\circ + b^\circ .\)
\(180^\circ - \left( {a^\circ + b^\circ } \right).\)
Trong các phát biểu sau, phát biểu nào là đúng
Mọi tứ giác đều nội tiếp được đường tròn.
Trong một tứ giác nội tiếp, tổng số đo hai góc đối bằng \(90^\circ \).
Tứ giác có tổng hai góc bằng \(180^\circ \) thì tứ giác đó nội tiếp.
Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới hai góc bằng nhau thì tứ giác đó nội tiếp.
Tứ giác \(ABCD\) nội tiếp đường tròn có hai cạnh đối \(AB\) và \(CD\) cắt nhau tại \(M\) và \(\widehat {BDA} = 80^\circ \) thì \(\widehat {BCM} = \)?
\(100^\circ \)
\(40^\circ \)
\(70^\circ \)
\(80^\circ \)
Cho tứ giác \[ABCD\]nội tiếp đường tròn \[\left( {O\,;\,R} \right)\]có \[AB = BC = R\]. Số đo \[\widehat {ABC}\] là:
\[120^\circ \]
\[140^\circ \]
\[70^\circ \]
\[60^\circ \]
Tứ giác \(ABCD\) nội tiếp đường tròn có hai cạnh đối \(AB\) và \(CD\) cắt nhau tại \(M\) và \(\widehat {BDA} = 80^\circ \) thì \(\widehat {BCM} = \)?
\(100^\circ \)
\(40^\circ \)
\(70^\circ \)
\(80^\circ \)
Trong các hình sau, hình nào sau đây không nội tiếp được đường tròn?
Hình vuông.
Hình chữ nhật.
Hình thoi có một góc nhọn.
Hình thang cân.
Cho tứ giác\[ABCD\] nội tiếp được đường tròn. Biết \(\widehat {C\,} = 60^\circ ,{\rm{ }}\widehat {\rm{D}} = 80^\circ \). Khi đó:
\(\widehat {A\,\,} = 60^\circ ;{\rm{ }}\widehat {B\,} = 80^\circ \)
\(\widehat {A\,\,} = 120^\circ ;{\rm{ }}\widehat {\rm{B}} = 100^\circ \)
\(\widehat A = 120^\circ ;{\rm{ }}\widehat {\rm{B}} = 130^\circ \)
\(\widehat A = 90^\circ ;{\rm{ }}\widehat B = 100^\circ \)
Trong các hình sau, hình nào sau đây không nội tiếp được đường tròn?
Hình vuông.
Hình chữ nhật.
Hình thoi có một góc nhọn.
Hình thang cân.
Cho tứ giác\[ABCD\] nội tiếp được đường tròn. Biết \[\widehat A = 50^\circ ,{\rm{ }}\widehat B = 70^\circ \]. Khi đó:
\(\widehat C = 110^\circ ;{\rm{ }}\widehat D = 70^\circ \)
\(\widehat C = 130^\circ ;{\rm{ }}\widehat D = 110^\circ \)
\(\widehat C = 40^\circ ;{\rm{ }}\widehat D = 130^\circ \)
\(\widehat C = 50^\circ ;{\rm{ }}\widehat D = 70^\circ \)
Trong các hình vẽ tứ giác\[ABCD\]sau hãy chọn hình vẽ có tứ giác nội tiếp trong đường tròn.
![Trong các hình vẽ tứ giác\[ABCD\]sau hãy chọn hình vẽ có tứ giác nội tiếp trong đường tròn. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid14-1755532706.png)
Hình I
Hình II
Hình III
Hình IV
Cho tứ giác\[ABCD\] nội tiếp được đường tròn. Biết \[\widehat A = 50^\circ ,{\rm{ }}\widehat B = 70^\circ \]. Khi đó:
\(\widehat C = 110^\circ ;{\rm{ }}\widehat D = 70^\circ \)
\(\widehat C = 130^\circ ;{\rm{ }}\widehat D = 110^\circ \)
\(\widehat C = 40^\circ ;{\rm{ }}\widehat D = 130^\circ \)
\(\widehat C = 50^\circ ;{\rm{ }}\widehat D = 70^\circ \)
Cho tứ giác \[MNPQ\] nội tiếp đường tròn \[(O;R)\] và có \[\widehat M = 50^\circ \]. Khi đó ta có:
\[\widehat P = 50^\circ \]
\[\widehat P = 130^\circ \]
\[\widehat P = 180^\circ \]
\[\widehat P = 310^\circ \]
Trong các phát biểu sau, phát biểu nào là đúng
Mọi tứ giác đều nội tiếp được đường tròn.
Trong một tứ giác nội tiếp, tổng số đo hai góc đối bằng \(90^\circ \).
Tứ giác có tổng hai góc bằng \(180^\circ \) thì tứ giác đó nội tiếp.
Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới hai góc bằng nhau thì tứ giác đó nội tiếp.
Cho tứ giác \[MNPQ\] nội tiếp đường tròn \[(O;R)\] và có \[\widehat M = 50^\circ \]. Khi đó ta có:
\[\widehat P = 50^\circ \]
\[\widehat P = 130^\circ \]
\[\widehat P = 180^\circ \]
\[\widehat P = 310^\circ \]
Cho hình vẽ sau:
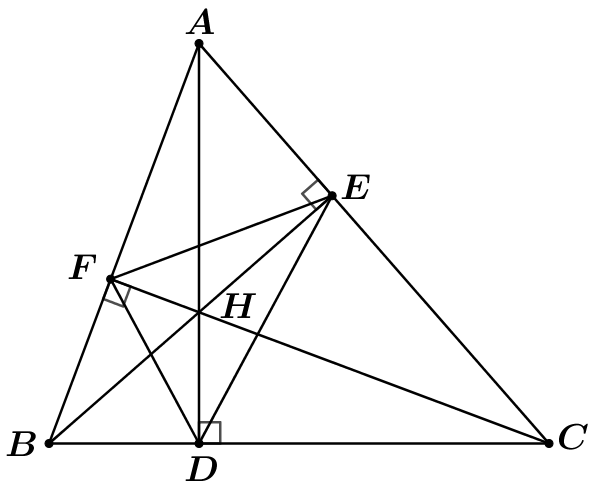
Số tứ giác nội tiếp được trong đường tròn là:
Có \[3\] hình tứ giác nội tiếp.
Có \[4\] hình tứ giác nội tiếp.
Có \[5\]hình tứ giác nội tiếp.
Có \[6\] hình tứ giác nội tiếp.
Tứ giác \(ABCD\) nội tiếp đường tròn có hai cạnh đối \(AB\) và \(CD\) cắt nhau tại \(M\) và \(\widehat {BDA} = 80^\circ \) thì \(\widehat {BCM} = \)?
\(100^\circ \)
\(40^\circ \)
\(70^\circ \)
\(80^\circ \)
Cho hình vẽ sau:
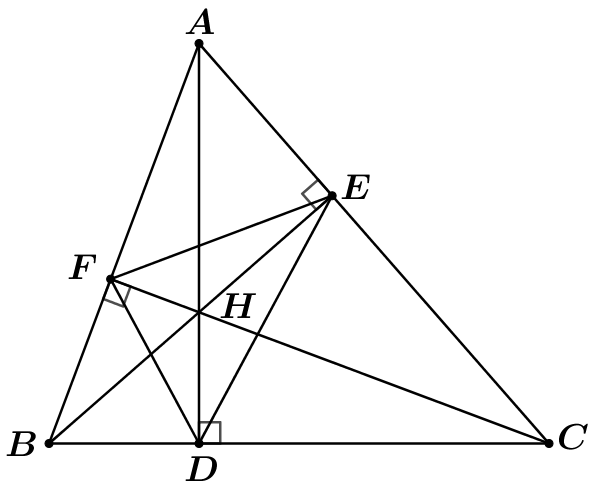
Số tứ giác nội tiếp được trong đường tròn là:
Có \[3\] hình tứ giác nội tiếp.
Có \[4\] hình tứ giác nội tiếp.
Có \[5\]hình tứ giác nội tiếp.
Có \[6\] hình tứ giác nội tiếp.
Cho tứ giác\[ABCD\] nội tiếp đường tròn \[\left( O \right)\]\(\;\)có hai tia\[AB;DC\] kéo dài cắt nhau tại \[M\]sao cho \[\widehat {AMD} = 20^\circ \] và hai tia\[AD;BC\] kéo dài cắt nhau tại \[N\] sao cho \[\widehat {ANB} = 40^\circ \]. Khi đó số đo của\[\widehat {BAD}\] là
\[120^\circ \]
\[40^\circ \]
\[20^\circ \]
\[60^\circ \]
Trong các hình sau, hình nào sau đây không nội tiếp được đường tròn?
Hình vuông.
Hình chữ nhật.
Hình thoi có một góc nhọn.
Hình thang cân.
Cho tứ giác\[ABCD\] nội tiếp đường tròn \[\left( O \right)\]\(\;\)có hai tia\[AB;DC\] kéo dài cắt nhau tại \[M\]sao cho \[\widehat {AMD} = 20^\circ \] và hai tia\[AD;BC\] kéo dài cắt nhau tại \[N\] sao cho \[\widehat {ANB} = 40^\circ \]. Khi đó số đo của\[\widehat {BAD}\] là
\[120^\circ \]
\[40^\circ \]
\[20^\circ \]
\[60^\circ \]
Cho tứ giác \[MNPQ\] có \[\widehat {PMQ} = \widehat {PNQ} = 90^\circ \] và \[MP = MQ.\] Khi đó số đo \[\widehat {MNP}\] là
\[45^\circ \]
\[90^\circ \]
\[125^\circ \]
\[135^\circ \].
Cho tứ giác\[ABCD\] nội tiếp được đường tròn. Biết \[\widehat A = 50^\circ ,{\rm{ }}\widehat B = 70^\circ \]. Khi đó:
\(\widehat C = 110^\circ ;{\rm{ }}\widehat D = 70^\circ \)
\(\widehat C = 130^\circ ;{\rm{ }}\widehat D = 110^\circ \)
\(\widehat C = 40^\circ ;{\rm{ }}\widehat D = 130^\circ \)
\(\widehat C = 50^\circ ;{\rm{ }}\widehat D = 70^\circ \)
Cho tứ giác \[MNPQ\] có \[\widehat {PMQ} = \widehat {PNQ} = 90^\circ \] và \[MP = MQ.\] Khi đó số đo \[\widehat {MNP}\] là
\[45^\circ \]
\[90^\circ \]
\[125^\circ \]
\[135^\circ \].
Cho đường tròn \[\left( O \right)\]. Biết \[MA;MB\] là các tiếp tuyến của \[\left( O \right)\] cắt nhau tại \[M\] và \[\widehat {AMB} = 58^\circ .\] Khi đó số đo \[\widehat {ABO}\] \(\;\)bằng
\[24^\circ .\]
\[29^\circ .\]
\[30^\circ .\]
\[31^\circ .\]
Cho tứ giác \[MNPQ\] nội tiếp đường tròn \[(O;R)\] và có \[\widehat M = 50^\circ \]. Khi đó ta có:
\[\widehat P = 50^\circ \]
\[\widehat P = 130^\circ \]
\[\widehat P = 180^\circ \]
\[\widehat P = 310^\circ \]
Cho đường tròn \[\left( O \right)\]. Biết \[MA;MB\] là các tiếp tuyến của \[\left( O \right)\] cắt nhau tại \[M\] và \[\widehat {AMB} = 58^\circ .\] Khi đó số đo \[\widehat {ABO}\] \(\;\)bằng
\[24^\circ .\]
\[29^\circ .\]
\[30^\circ .\]
\[31^\circ .\]
Cho hình vẽ bên dưới. Biết \[AD\,\]// \(BC\). Số đo góc \[x\] bằng:
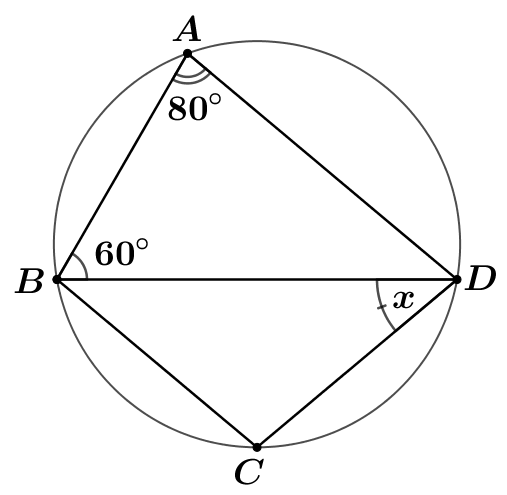
\[40^\circ .\]
\[70^\circ .\]
\[60^\circ .\]
\[50^\circ .\]
Cho hình vẽ sau:
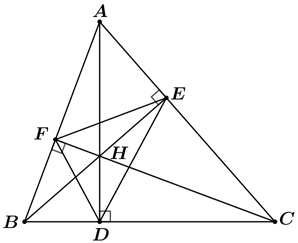
Số tứ giác nội tiếp được trong đường tròn là:
Có \[3\] hình tứ giác nội tiếp.
Có \[4\] hình tứ giác nội tiếp.
Có \[5\]hình tứ giác nội tiếp.
Có \[6\] hình tứ giác nội tiếp.
Cho hình vẽ bên dưới. Biết \[AD\,\]// \(BC\). Số đo góc \[x\] bằng:
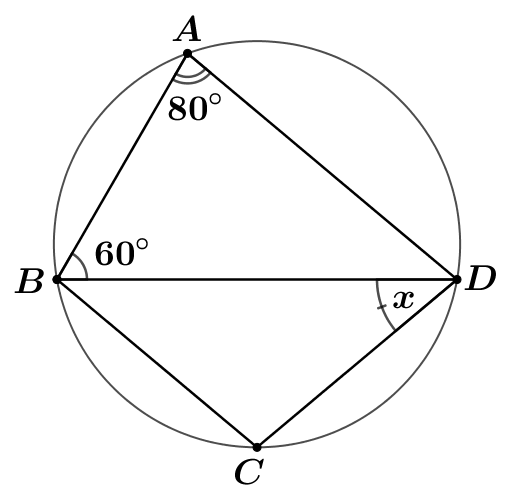
\[40^\circ .\]
\[70^\circ .\]
\[60^\circ .\]
\[50^\circ .\]
Cho 4 điểm \[M,Q,N,P\]thuộc \[\left( O \right)\]. Biết \[\widehat {MNP} = 60^\circ ;\,\,\widehat {QMP} = 40^\circ \]. Khi đó số đo \[\widehat {MPQ}\] là:
\[20^\circ .\]
B.
\[30^\circ .\]
\[40^\circ .\]
Cho tứ giác\[ABCD\] nội tiếp đường tròn \[\left( O \right)\]\(\;\)có hai tia\[AB;DC\] kéo dài cắt nhau tại \[M\]sao cho \[\widehat {AMD} = 20^\circ \] và hai tia\[AD;BC\] kéo dài cắt nhau tại \[N\] sao cho \[\widehat {ANB} = 40^\circ \]. Khi đó số đo của\[\widehat {BAD}\] là
\[120^\circ \]
\[40^\circ \]
\[20^\circ \]
\[60^\circ \]
Cho 4 điểm \[M,Q,N,P\]thuộc \[\left( O \right)\]. Biết \[\widehat {MNP} = 60^\circ ;\,\,\widehat {QMP} = 40^\circ \]. Khi đó số đo \[\widehat {MPQ}\] là:
\[20^\circ .\]
B.
\[30^\circ .\]
\[40^\circ .\]
Cho tứ giác \[ABCD\]có \[\widehat A:\widehat B:\widehat C:\widehat D = 8:15:28:21\] khẳng định nào sau đây là đúng:
Tứ giác \[ABCD\] là tứ giác nội tiếp.
Tứ giác \[ABCD\] không nội tiếp được.
Tứ giác \[ABCD\] là một hình thoi.
Tứ giác \[ABCD\] là một hình thang cân.
Cho tứ giác \[MNPQ\] có \[\widehat {PMQ} = \widehat {PNQ} = 90^\circ \] và \[MP = MQ.\] Khi đó số đo \[\widehat {MNP}\] là
\[45^\circ \]
\[90^\circ \]
\[125^\circ \]
\[135^\circ \].
Cho tứ giác \[ABCD\]có \[\widehat A:\widehat B:\widehat C:\widehat D = 8:15:28:21\] khẳng định nào sau đây là đúng:
Tứ giác \[ABCD\] là tứ giác nội tiếp.
Tứ giác \[ABCD\] không nội tiếp được.
Tứ giác \[ABCD\] là một hình thoi.
Tứ giác \[ABCD\] là một hình thang cân.
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\). Biết \(\widehat {ADO\,} = \,50^\circ \);\(\widehat {OCD}\, = \,40^\circ \). Khi đó
số đo \[\widehat {ABC}\] là
\[40^\circ \]
\[50^\circ \]
\[90^\circ \]
\[10^\circ \]
Cho đường tròn \[\left( O \right)\]. Biết \[MA;MB\] là các tiếp tuyến của \[\left( O \right)\] cắt nhau tại \[M\] và \[\widehat {AMB} = 58^\circ .\] Khi đó số đo \[\widehat {ABO}\] \(\;\)bằng
\[24^\circ .\]
\[29^\circ .\]
\[30^\circ .\]
\[31^\circ .\]
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\). Biết \(\widehat {ADO\,} = \,50^\circ \);\(\widehat {OCD}\, = \,40^\circ \). Khi đó
số đo \[\widehat {ABC}\] là
\[40^\circ \]
\[50^\circ \]
\[90^\circ \]
\[10^\circ \]
Cho tứ giác \(A;\,B;\,C;\,D\) thuộc \[\left( O \right)\]. Biết \[\widehat {AOC}\, = \,120^\circ \]. Khi đó số đo \[\widehat {ADC}\] là:
\[60^\circ \] hoặc \[120^\circ .\]
\[80^\circ .\]
\[100^\circ \]
\[120^\circ \]
Cho hình vẽ bên dưới. Biết \[AD\,\]// \(BC\). Số đo góc \[x\] bằng:
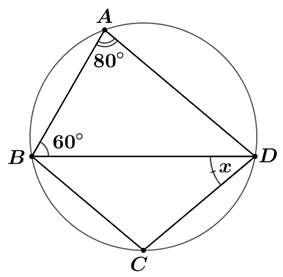
\[40^\circ .\]
\[70^\circ .\]
\[60^\circ .\]
\[50^\circ .\]
Cho tứ giác \(A;\,B;\,C;\,D\) thuộc \[\left( O \right)\]. Biết \[\widehat {AOC}\, = \,120^\circ \]. Khi đó số đo \[\widehat {ADC}\] là:
\[60^\circ \] hoặc \[120^\circ .\]
\[80^\circ .\]
\[100^\circ \]
\[120^\circ \]
Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Gọi \(H\) là điểm nằm giữa \(O\) và \(B\). Kẻ dây \(CD \bot AB\) tại \(H\). Trên cung nhỏ \(AC\) lấy điểm \(E\), kẻ \(CK \bot AE\) tại \(K\). Đường thẳng \(DE\) cắt \(CK\) tại \(F\). Tam giác \(ACF\) là tam giác
cân tại \(F\).
cân tại \(C\).
cân tại \(A\).
đều.
Cho 4 điểm \[M,Q,N,P\]thuộc \[\left( O \right)\]. Biết \[\widehat {MNP} = 60^\circ ;\,\,\widehat {QMP} = 40^\circ \]. Khi đó số đo \[\widehat {MPQ}\] là:
\[20^\circ .\]
B.
\[30^\circ .\]
\[40^\circ .\]
Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Gọi \(H\) là điểm nằm giữa \(O\) và \(B\). Kẻ dây \(CD \bot AB\) tại \(H\). Trên cung nhỏ \(AC\) lấy điểm \(E\), kẻ \(CK \bot AE\) tại \(K\). Đường thẳng \(DE\) cắt \(CK\) tại \(F\). Tam giác \(ACF\) là tam giác
cân tại \(F\).
cân tại \(C\).
cân tại \(A\).
đều.
Cho \[\Delta ABC\] cân tại \[A\] có \[\widehat B = 40^\circ \] điểm\[D\] thuộc cạnh \[AB\]. Đường vuông góc với \[AB\] tại \[D\] cắt \[BC\] tại \[E\] và cắt đường thẳng vuông góc với \[AC\] tại \[C\] ở \[K\]. Gọi \[I\] là trung điểm của \[BE\]. Khi đó số đo \[\widehat {IAK}\] là
\[40^\circ \]
\[50^\circ \]
\[90^\circ \]
\[60^\circ \]
Cho tứ giác \[ABCD\]có \[\widehat A:\widehat B:\widehat C:\widehat D = 8:15:28:21\] khẳng định nào sau đây là đúng:
Tứ giác \[ABCD\] là tứ giác nội tiếp.
Tứ giác \[ABCD\] không nội tiếp được.
Tứ giác \[ABCD\] là một hình thoi.
Tứ giác \[ABCD\] là một hình thang cân.
Cho \[\Delta ABC\] cân tại \[A\] có \[\widehat B = 40^\circ \] điểm\[D\] thuộc cạnh \[AB\]. Đường vuông góc với \[AB\] tại \[D\] cắt \[BC\] tại \[E\] và cắt đường thẳng vuông góc với \[AC\] tại \[C\] ở \[K\]. Gọi \[I\] là trung điểm của \[BE\]. Khi đó số đo \[\widehat {IAK}\] là
\[40^\circ \]
\[50^\circ \]
\[90^\circ \]
\[60^\circ \]
Cho tứ giác \[ABCD\] nội tiếp đường tròn tâm \(O\) bán kính \[a\]. Biết rằng \[AC \bot BD\]. Khi đó để\[AB + CD\] đạt giá trị lớn nhất thì
\[AC = AB\]
\[AC = BD\]
\[DB = AB\]
Không có đáp án đúng.
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\). Biết \(\widehat {ADO\,} = \,50^\circ \);\(\widehat {OCD}\, = \,40^\circ \). Khi đó
số đo \[\widehat {ABC}\] là
\[40^\circ \]
\[50^\circ \]
\[90^\circ \]
\[10^\circ \]
Cho tứ giác \[ABCD\] nội tiếp đường tròn tâm \(O\) bán kính \[a\]. Biết rằng \[AC \bot BD\]. Khi đó để\[AB + CD\] đạt giá trị lớn nhất thì
\[AC = AB\]
\[AC = BD\]
\[DB = AB\]
Không có đáp án đúng.
Cho tứ giác \(A;\,B;\,C;\,D\) thuộc \[\left( O \right)\]. Biết \[\widehat {AOC}\, = \,120^\circ \]. Khi đó số đo \[\widehat {ADC}\] là:
\[60^\circ \] hoặc \[120^\circ .\]
\[80^\circ .\]
\[100^\circ \]
\[120^\circ \]
Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Gọi \(H\) là điểm nằm giữa \(O\) và \(B\). Kẻ dây \(CD \bot AB\) tại \(H\). Trên cung nhỏ \(AC\) lấy điểm \(E\), kẻ \(CK \bot AE\) tại \(K\). Đường thẳng \(DE\) cắt \(CK\) tại \(F\). Tam giác \(ACF\) là tam giác
cân tại \(F\).
cân tại \(C\).
cân tại \(A\).
đều.
Cho \[\Delta ABC\] cân tại \[A\] có \[\widehat B = 40^\circ \] điểm \[D\] thuộc cạnh \[AB\]. Đường vuông góc với \[AB\] tại \[D\] cắt \[BC\] tại \[E\] và cắt đường thẳng vuông góc với \[AC\] tại \[C\] ở \[K\]. Gọi \[I\] là trung điểm của \[BE\]. Khi đó số đo \[\widehat {IAK}\] là
\[40^\circ \]
\[50^\circ \]
\[90^\circ \]
\[60^\circ \]
Cho tứ giác \[ABCD\] nội tiếp đường tròn tâm \(O\) bán kính \[a\]. Biết rằng \[AC \bot BD\]. Khi đó để\[AB + CD\] đạt giá trị lớn nhất thì
\[AC = AB\]
\[AC = BD\]
\[DB = AB\]
Không có đáp án đúng.