41 câu hỏi
Đường tròn tiếp xúc với ba cạnh của tam giác là
đường tròn ngoại tiếp tam giác.
đường tròn đi qua ba đỉnh của tam giác.
đường tròn nội tiếp tam giác.
đường tròn bàng tiếp tam giác.
Đường tròn nội tiếp tam giác là đường tròn
cắt ba cạnh của tam giác.
đi qua ba đỉnh của tam giác.
tiếp xúc với hai cạnh của tam giác.
tiếp xúc với ba cạnh của tam giác.
Tam giác \(ABC\) ngoại tiếp đường tròn tâm \(I\) khi đường tròn tâm \(I\)
cắt ba cạnh của tam giác \(ABC\).
nội tiếp tam giác \(ABC\).
đi qua ba đỉnh của tam giác \(ABC\).
ngoại tiếp tam giác \(ABC\).
Đường tròn ngoại tiếp tam giác là đường tròn
tiếp xúc với ba cạnh của tam giác đó.
Đi qua ba đỉnh của tam giác đó.
cắt ba cạnh của tam giác đó.
Đi qua trọng tâm của tam giác đó.
Đường tròn ngoại tiếp tam giác vuông có bán kính bằng
nửa cạnh huyền của tam giác vuông đó.
cạnh huyền của tam giác vuông đó.
hai lần cạnh huyền của tam giác vuông đó.
độ dài một cạnh góc vuông của tam giác vuông đó.
Đường tròn ngoại tiếp tam giác có tâm là
giao điểm của ba đường cao.
giao điểm của ba đường trung tuyến.
giao điểm của ba đường phân giác.
giao điểm của ba đường trung trực.
Số đường tròn ngoại tiếp một tam giác là
\(1\).
\(2\).
\(3\).
\(0\).
Tâm của đường tròn ngoại tiếp tam giác vuông
nằm trong tam giác đó.
là trung điểm cạnh huyền.
nằm ngoài tam giác đó.
là trung điểm cạnh nhỏ nhất.
Tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) nếu
tâm \(O\) là giao điểm của ba đường trung tuyến của tam giác \(ABC\).
đường tròn \(\left( O \right)\) tiếp xúc với ba cạnh của tam giác \(ABC\).
đường tròn \(\left( O \right)\) đi qua ba đỉnh của tam giác \(ABC\).
tâm \(O\) là giao điểm của ba đường phân giác trong của tam giác \(ABC\).
Cho \(O\) là giao điểm ba đường trung trực của tam giác. Chọn khẳng định sai.
\(O\) nằm trong tam giác nếu tam giác nhọn.
\(O\) là trung điểm cạnh huyền nếu tam giác vuông.
\(O\) nằm ngoài tam giác nếu tam giác tù.
\(O\) cách đều ba cạnh của tam giác.
Cho đường tròn tâm \(O\) đường kính \(AB\). \(I\) là một điểm tùy ý nằm trên đường tròn (\(I\) khác \(A\) và \(B\)). Chọn đáp án đúng.
Tam giác \(IAB\) là tam giác nhọn.
Tam giác \(IAB\) là tam giác tù.
Tam giác \(IAB\) là tam giác vuông.
Tam giác \(IAB\) là tam giác cân.
Cho tam giác \(\Delta ABC\) có \(AB = 13\,{\rm{cm}}\); \(AC = 12\,{\rm{cm}}\); \(BC = 5\,{\rm{cm}}\). Khẳng định nào sau đây sai? Tâm của đường tròn ngoại tiếp tam giác \(ABC\) là
trung điểm cạnh \(AB\).
điểm nằm trên cạnh\(AB\)và cách \(A\) một khoảng bằng \[6,5\,{\rm{cm}}\].
giao ba đường trung trực của tam giác \(ABC\).
trung điểm cạnh \(CB\).
Cho tam giác \(ABC\) có \(AB = 3\,{\rm{cm}}\); \(AC = 4\,{\rm{cm}}\); \(BC = 5\,{\rm{cm}}\). Chọn khẳng định sai.
\(\Delta \,ABC\) vuông tại \(A\).
Điểm \(B\) thuộc đường tròn đường kính \(AC\).
Đường tròn ngoại tiếp \(\Delta ABC\) có tâm là trung điểm cạnh \(BC\).
Điểm \(A\) thuộc đường tròn đường kính \(BC\).
Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác thì tam giác đó là
tam giác đều.
Tam giác vuông.
Tam giác tù.
D. Tam giác cân.
Tính bán kính \(R\) của đường tròn ngoại tiếp hình chữ nhật \(ABCD\), biết đường chéo \(AC = 8\,{\rm{cm}}\).
\(R = 8\sqrt 2 \,{\rm{cm}}\).
\(R = 4\,{\rm{cm}}\).
\(R = \frac{{8\sqrt 2 }}{2}\,{\rm{cm}}\).
\(R = \frac{{8\sqrt 3 }}{2}\,{\rm{cm}}\).
Tính bán kính \(R\) của đường tròn ngoại tiếp hình chữ nhật \(ABCD\), biết đường chéo \(BD = 6\sqrt 2 {\rm{cm}}{\rm{.}}\)
\(R = 3\sqrt 2 \,{\rm{cm}}\).
\(R = 6\,{\rm{cm}}\).
\(R = 3\,{\rm{cm}}\).
\(R = \frac{3}{{\sqrt 2 }}\,{\rm{cm}}\).
Tính bán kính \(R\) của đường tròn ngoại tiếp hình vuông \(ABCD\), biết đường chéo \(AC = 5\sqrt 2 \,{\rm{cm}}{\rm{.}}\)
\(R = 5\sqrt 2 \,{\rm{cm}}\).
\(R = \frac{{5\sqrt 2 }}{2}\,\,{\rm{cm}}\).
\(R = 5\,\,{\rm{cm}}\).
\(R = \frac{{5\sqrt 3 }}{2}\,\,{\rm{cm}}\).
Tính bán kính \(R\) của đường tròn ngoại tiếp hình vuông \(ABCD\) có đường chéo \(7\sqrt 2 \,{\rm{cm}}\).
\(R = 7\sqrt 2 \,\,{\rm{cm}}\).
\(R = \frac{{7\sqrt 3 }}{2}\,\,{\rm{cm}}\).
\(R = 7\,{\rm{cm}}\).
\(R = \frac{{7\sqrt 2 }}{2}\,\,{\rm{cm}}\).
Cho hình chữ nhật \[GHIK\] gọi \(O\) là giao điểm của hai đường chéo. Câu nào sau đây đúng?
Bốn điểm \(G;\,H;\,I;\,K\)cùng thuộc đường tròn tâm \(G\).
Bốn điểm \(G;\,H;\,I;\,K\)cùng thuộc đường tròn tâm \(K\).
Bốn điểm \(G;\,H;\,I;\,K\) cùng thuộc đường tròn tâm \(I\).
Bốn điểm \(G;\,H;\,I;\,K\)cùng thuộc đường tròn tâm \(O\).
Tâm đường tròn ngoại tiếp hình chữ nhật có hai kích thước \(3\,{\rm{cm}}\) và \(4\,{\rm{cm}}\)là
giao điểm hai đường chéo của hình chữ nhật và cách mỗi đỉnh một khoảng bằng \(3\,{\rm{cm}}\).
giao điểm hai đường chéo của hình chữ nhật và cách mỗi đỉnh một khoảng bằng \(2,5\,{\rm{cm}}\).
giao điểm hai đường chéo của hình chữ nhật và cách mỗi đỉnh một khoảng bằng \(4\,{\rm{cm}}\).
giao điểm hai đường chéo của chữ nhật và cách mỗi đỉnh một khoảng bằng \(5\,{\rm{cm}}\).
Tâm đường tròn ngoại tiếp hình vuông\(ABCD\) cạnh\[5\,{\rm{cm}}\]là
điểm nằm trên cạnh \(AC\) và cách \(A\) một khoảng bằng \[5\,{\rm{cm}}\].
điểm nằm trên cạnh \(AC\) và cách \(A\) một khoảng bằng \[2,5\,{\rm{cm}}\].
điểm nằm trên cạnh \(AC\) và cách \(A\) một khoảng bằng \[5\sqrt 2 \,{\rm{cm}}\].
điểm nằm trên cạnh \(AC\) và cách \(A\) một khoảng bằng \[\frac{{5\sqrt 2 }}{2}\,{\rm{cm}}\].
Cho hình chữ nhật \(ABCD\) có \(AB = 12\,{\rm{cm}},BC = 5\,{\rm{cm}}\). Tính bán kính đường tròn ngoại tiếp hình chữ nhật \(ABCD\)
\(R = 7,5\,{\rm{cm}}\).
\(R = 13\,{\rm{cm}}\).
\(R = 6\,{\rm{cm}}\).
\(R = 6,5\,{\rm{cm}}\).
Tính bán kính \(R\) của đường tròn ngoại tiếp hình vuông \(ABCD\) cạnh \(3\,{\rm{cm}}\).
\(R = 3\sqrt 2 \,{\rm{cm}}\).
\(R = \frac{{3\sqrt 2 }}{2}\,{\rm{cm}}\).
\(R = 3\,{\rm{cm}}\).
\(R = \frac{{3\sqrt 3 }}{2}\,{\rm{cm}}\).
Đường tròn tâm \(I\) nội tiếp tam giác đều \(PQR\) có cạnh bằng \(5{\rm{ cm}}\), khi đó bán kính đường tròn tâm \(I\) bằng
\(\frac{{5\sqrt 3 }}{2}\,{\rm{cm}}\).
\(\frac{{5\sqrt 3 }}{6}\,{\rm{cm}}\).
\(5\sqrt 3 \,{\rm{cm}}\).
\(\frac{{5\sqrt 3 }}{3}\,{\rm{cm}}\).
Đường tròn tâm \(I'\) nội tiếp tam giác đều \(A'B'C'\) có cạnh bằng \(4\,{\rm{cm}}\). Khi đó đường kính đường tròn tâm \(I'\) bằng
\(\frac{{4\sqrt 3 }}{6}\,{\rm{cm}}\).
\(\frac{{4\sqrt 3 }}{3}\,{\rm{cm}}\).
\(4\sqrt 3 \,{\rm{cm}}\).
\(\frac{{8\sqrt 3 }}{3}\,{\rm{cm}}\).
Đường tròn tâm \(I\) nội tiếp tam giác đều \(ABC\) có bán kính bằng \(2\,{\rm{cm}}\). Khi đó độ dài cạnh \(AB\) bằng
\(2\sqrt 3 \,{\rm{cm}}\).
\(\frac{{12\sqrt 3 }}{6}\,{\rm{cm}}\).
\(4\sqrt 3 \,{\rm{cm}}\).
\(\frac{{4\sqrt 3 }}{3}\,{\rm{cm}}\).
Đường tròn tâm \(O\) nội tiếp tam giác đều \(ABC\) có đường kính bằng \(7\,{\rm{cm}}\). Khi đó độ dài cạnh \(AB\) bằng
\(2\sqrt 3 \,{\rm{cm}}\).
\(\frac{{\sqrt 3 }}{7}\,{\rm{cm}}\).
\(7\sqrt 3 \,{\rm{cm}}\).
\(\frac{{7\sqrt 3 }}{3}\,{\rm{cm}}\).
Tam giác đều \(ABC\) có cạnh bằng \(7\,{\rm{cm}}\). Chu vi của đường tròn nội tiếp tam giác đều \(ABC\):
\(7\pi \sqrt 3 \,{\rm{cm}}\).
\(\frac{{7\sqrt 3 }}{3}\,{\rm{cm}}\).
\(\frac{{7\pi \sqrt 3 }}{3}\,{\rm{c}}{{\rm{m}}^2}\).
\(\frac{{7\pi \sqrt 3 }}{3}\,{\rm{cm}}\).
Tam giác đều có cạnh \(3\,{\rm{cm}}\). Đường kính đường tròn ngoại tiếp tam giác đó bằng:
\(2\sqrt 3 \,{\rm{cm}}\).
\(\sqrt 3 \,{\rm{cm}}\).
\(\frac{{2\sqrt 3 }}{3}\,{\rm{cm}}\).
\(\frac{{\sqrt 3 }}{2}\,{\rm{cm}}\).
Cho tam giác \[ABC\] vuông tại \[A\] với \[AB = 18\,{\rm{cm}}\], \[AC = 24\,{\rm{cm}}\]. Bán kính đường tròn ngoại tiếp tam giác đó là
\[30\,\,({\rm{cm)}}\]
\[10\,\,({\rm{cm)}}\].
\[20\,\,({\rm{cm)}}\].
\[15\,\,({\rm{cm)}}\].
Xác định tâm và bán kính của đường tròn đi qua cả ba đỉnh của tam giác \(ABC\) vuông tại \(A\); \(AB = AC = a\).
Tâm là \(A\) và bán kính \(R = a\sqrt 2 \).
Tâm là trung điểm cạnh huyền \(AC\) và bán kính \(R = a\sqrt 2 \).
Tâm là trung điểm cạnh huyền \(BC\) và bán kính \(R = \frac{{a\sqrt 2 }}{2}\).
Tâm là điểm \(B\) và bán kính là \(R = \frac{{a\sqrt 2 }}{2}\).
Tính diện tích của tam giác đều nội tiếp \(\left( {O\;;\;4\,{\rm{cm}}} \right)\).
\[24\,\,({\rm{c}}{{\rm{m}}^2})\].
\[24\sqrt 3 \,\,({\rm{c}}{{\rm{m}}^2})\].
\[12\,\,({\rm{c}}{{\rm{m}}^2})\].
\[12\sqrt 3 \,\,({\rm{c}}{{\rm{m}}^2})\].
Tam giác \(ABC\) đều có đường trung tuyến \(AM\) nội tiếp đường tròn \(\left( {O\;;\;4\,{\rm{cm}}} \right)\). Độ dài \(AM\) bằng:
\[\frac{8}{3}\,\,({\rm{cm}})\].
\[8\,\,({\rm{cm}})\].
\[6\,\,({\rm{cm}})\].
\[4\,\,({\rm{cm}})\].
Tam giác \(ABC\) vuông tại \(A\) nội tiếp đường tròn \(\left( {O\;;\;7,5\,{\rm{cm}}} \right)\). Biết \(\frac{{AB}}{{AC}} = \frac{3}{4}\). Chu vi \(\Delta ABC\) là:
\[15\,\,({\rm{cm}})\].
\[36\,\,({\rm{cm}})\].
\[14,5\,\,({\rm{cm}})\].
\[7,5\,\,({\rm{cm}})\].
Tam giác đều \(IHK\) nội tiếp đường tròn có chu vi bằng \(27\,{\rm{cm}}\). Khi đó, bán kính của đường tròn nội tiếp tam giác đều \(IHK\) là
\(\frac{{3\sqrt 3 }}{3}\,{\rm{cm}}\).
\(3\sqrt 3 \,{\rm{cm}}\).
\(\frac{{3\sqrt 3 }}{2}\,{\rm{cm}}\).
\(\frac{{9\sqrt 3 }}{2}\,{\rm{cm}}\).
Một mảnh vườn có dạng hình tam giác đều \(MNP\) cạnh \(10\,{\rm{m}}\). Người ta muốn trồng hoa ở phần đất bên trong đường tròn nội tiếp \(\Delta MNP\). Diện tích phần đất trồng hoa bằng:
\(\frac{{25\pi }}{3}\,{{\rm{m}}^2}\).
\(\frac{{25\sqrt 3 }}{3}\,{{\rm{m}}^2}\).
\(\frac{{25\pi }}{3}\,{{\rm{m}}^2}\).
\(\frac{{25\pi \sqrt 3 }}{9}\,{{\rm{m}}^2}\).
Gọi \(r\)và \(R\) lần lượt là bán kính đường tròn nội tiếp và đường tròn ngoại tiếp của một hình tam giác đều. Tỉ số \(\frac{r}{R}\) là:
\[\frac{1}{{\sqrt 3 }}\].
\[\frac{{\sqrt 3 }}{2}\].
\[\frac{1}{{\sqrt 2 }}\].
\[\frac{1}{2}\].
Tính độ dài của tam giác đều nội tiếp \[\left( {O\,;\,R} \right)\] theo \[R\].
\[\frac{R}{{\sqrt 3 }}\].
\[\sqrt 3 R\].
\[R\sqrt 6 \].
\[3R\].
Tính diện tích tam giác đều nội tiếp đường tròn \[\left( {O\,;\,2\,{\rm{cm}}} \right)\]
\[6\,{\rm{c}}{{\rm{m}}^2}\].
\[6\sqrt 3 \,{\rm{c}}{{\rm{m}}^2}\].
\[3\,{\rm{c}}{{\rm{m}}^2}\].
\[3\sqrt 3 \,{\rm{c}}{{\rm{m}}^2}\].
Cho \(\Delta ABC\) vuông tại \(A\) có: \[AB = 9 cm; AC = 12 cm\], bán kính đường tròn nội tiếp \(\Delta ABC\) bằng
\[2\,cm\].
\[3\,cm\].
\(6\,cm\).
\(12,5\,cm\).
Một khu dân cư được bao quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là \(900{\rm{ }}m\), \(1200{\rm{ }}m\)và \(1500{\rm{ }}m\). Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
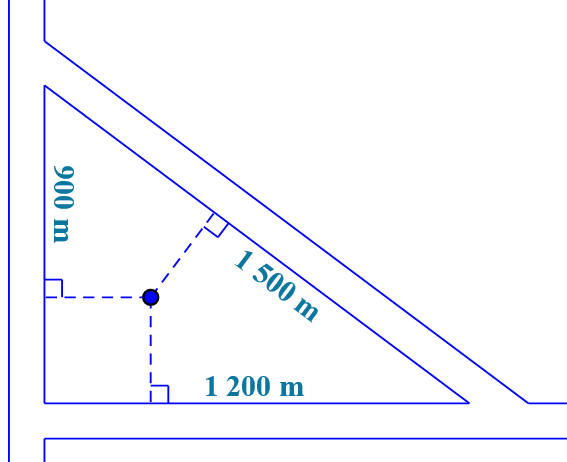
\[150\,m\].
\[300\,m\].
\[450\,m\].
\[500\,m\].
