50 câu hỏi
Cho hình trụ có chu vi đáy là \(8\pi \) và chiều cao \(h = 10\). Tính thể tích hình trụ.
\[80\pi \].
\[40\pi \].
\[160\pi \].
\[150\pi \].
Cho hình trụ có bán kính đáy \(R = 3\,(cm)\) và chiều cao \(h = 6\,(cm)\). Diện tích xung quanh của hình trụ là.
\[40\pi \].
\[36\pi \].
\[18\pi \].
\[24\pi \].
Cho hình trụ có bán kính đáy \(R = 4\,(cm)\) và chiều cao \(h = 5\,\,(cm)\). Diện tích xung quanh của hình trụ là.
\[40\pi \].
\[30\pi \].
\[20\pi \].
\[50\pi \].
Cho hình trụ có bán kính đáy \(R = 12\,\,(cm)\) và diện tích toàn phần \(672\pi \,\,(c{m^2})\). Tính chiều cao của hình trụ.
\[16{\mkern 1mu} cm\].
\[18{\mkern 1mu} cm\].
\[8{\mkern 1mu} cm\].
\[20{\mkern 1mu} cm\].
Cho hình trụ có bán kính đáy \(R = 12\,\,(cm)\) và diện tích toàn phần \(672\pi \,\,(c{m^2})\). Tính chiều cao của hình trụ.
\[16{\mkern 1mu} cm\].
\[18{\mkern 1mu} cm\].
\[8{\mkern 1mu} cm\].
\[20{\mkern 1mu} cm\].
Chọn câu đúng. Cho hình trụ có bán kính đáy \(R\) và chiều cao \(h\). Nếu ta giảm chiều cao đi \[9\] lần và tăng bán kính đáy lên \[3\] lần thì.
Thể tích hình trụ không đổi.
Diện tích toàn phần không đổi.
Diện tích xung quanh không đổi.
Chu vi đáy không đổi.
Chọn câu đúng. Cho hình trụ có bán kính đáy \(R\) và chiều cao \(h\). Nếu ta tăng chiều cao lên \[2\] lần và giảm bán kính đáy đi \[2\] lần thì.
Thể tích hình trụ không đổi.
Diện tích toàn phần không đổi.
Diện tích xung quanh không đổi.
Chu vi đáy không đổi.
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 10(cm)\) và đường kính đáy là \(d = 6cm\). Tính diện tích toàn phần của hộp sữa. Lấy \(\pi \simeq 3,14\).
\[110\pi \,\,(c{m^2})\].
\[129\pi \,\,(c{m^2})\].
\[96\pi {\mkern 1mu} \,\,(c{m^2})\].
\[69\pi {\mkern 1mu} \,\,(c{m^2})\].
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12\,cm\) và đường kính đáy là \(d = 8\,cm\). Tính diện tích toàn phần của hộp sữa. Lấy \(\pi \simeq 3,14\).
\[110\pi {\mkern 1mu} (c{m^2})\].
\[128\pi {\mkern 1mu} (c{m^2})\].
\[96\pi (c{m^2})\].
\[112\pi {\mkern 1mu} (c{m^2})\].
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy \(S = 25\pi \,c{m^2}\) và chiều cao \(h = 10cm\). Nếu trục lăn đủ \(12\) vòng thì diện tích tạo trên sân phẳng là bao nhiêu?
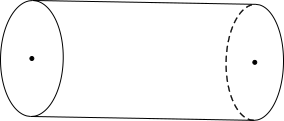
\[1200\pi {\mkern 1mu} (c{m^2})\].
\[600\pi {\mkern 1mu} (c{m^2})\].
\[1000\pi {\mkern 1mu} (c{m^2})\].
\[1210\pi {\mkern 1mu} (c{m^2})\].
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy \(S = 36\pi \,c{m^2}\) và chiều cao \(h = 8\,cm\). Nếu trục lăn đủ \(10\) vòng thì diện tích tạo trên sân phẳng là bao nhiêu?
\(1200\pi (c{m^2})\).
\(480\pi (c{m^2})\).
\[960\pi (c{m^2})\].
\[960{\mkern 1mu} (c{m^2})\].
Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là \(3\,cm\).
\[7{\mkern 1mu} cm\].
\[5{\mkern 1mu} cm\].
\[3{\mkern 1mu} cm\].
\[9{\mkern 1mu} cm\].
Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là \(4\,cm\).
\[2{\mkern 1mu} cm\].
\[4{\mkern 1mu} cm\].
\[1{\mkern 1mu} cm\].
\[8{\mkern 1mu} cm\].
Cho hình trụ bị cắt bỏ một phần \(OABB'A'O'\) như hình vẽ. Thể tích phần còn lại là:
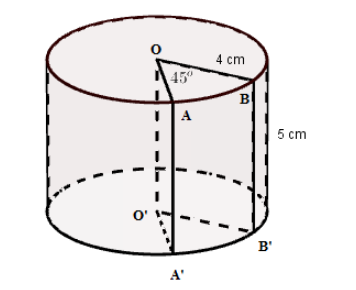
\[70\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[80\pi {\mkern 1mu} (c{m^3})\].
\[60\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[10\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
Cho hình trụ bị cắt bỏ một phần \(OABB'A'O'\) như hình vẽ. tính thể tích phần còn lại là:
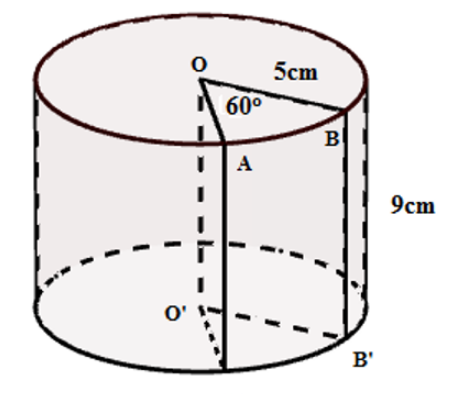
\[187,5\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[187\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[375\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[75\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
Một hình trụ có đường kính đáy và chiều cao đều bằng \[4\,{\rm{dm}}\]. Diện tích toàn phần của hình trụ bằng
\(12\pi \,{\rm{d}}{{\rm{m}}^{\rm{2}}}\).
\(24\pi \,{\rm{d}}{{\rm{m}}^{\rm{2}}}\).
\(48\pi \,{\rm{d}}{{\rm{m}}^{\rm{2}}}\).
\(64\pi \,{\rm{d}}{{\rm{m}}^{\rm{2}}}\).
Một hình trụ có diện tích đáy bằng \(20\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\), chiều cao bằng đường kính đáy. Diện tích xung quanh của hình trụ đó bằng bao nhiêu?
\(40\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(80\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(40\pi \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(80\pi \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Cho hai hình trụ. Hình trụ thứ nhất có bán kính đáy gấp 2 lần bán kính đáy của hình trụ thứ hai và có chiều cao bằng \(\frac{1}{4}\) chiều cao của hình trụ thứ hai. Tỉ số các thể tích của hình trụ thứ nhất và hình trụ thứ hai là
\(\frac{1}{2}\).
\(\frac{3}{2}\).
1.
2.
Để đo thể tích của một viên đá, người ta cho viên đá đó vào trong một chiếc bình hình trụ, rồi đổ nước cho ngập viên đá, khi đó mực nước trong bình cao \(18\,{\rm{cm}}\). Sau đó, người ta lấy viên đá ra khỏi bình, khi đó mực nước trong bình cao \(15\,{\rm{cm}}\). Biết rằng đường kính đáy của hình trụ bằng \(18\,{\rm{cm}}\). Thể tích của viên đá xấp xỉ bằng
\(763\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
\(679\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
\(170\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
\(254\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Cho hình nón có bán kính đáy \(R = 3\,(cm)\) và chiều cao \(h = 4\,(cm)\).
Diện tích xung quanh của hình nón là:
\[25\pi (c{m^2})\].
\[12\pi (c{m^2})\].
\[20\pi (c{m^2})\].
\[15\pi (c{m^2})\].
Cho hình nón có đường kính đáy \(d = 10cm\) và diện tích xung quanh\(65\pi \,(c{m^2})\). Tính thể tích khối nón.
\[100\pi {\mkern 1mu} (c{m^3})\].
\[120\pi {\mkern 1mu} (c{m^3})\].
\[300\pi {\mkern 1mu} (c{m^3})\].
\[200\pi (c{m^3})\].
Cho hình nón có đường kính đáy \(d = 18\,cm\) và diện tích xung quanh\(135\pi (c{m^2})\). Tính thể tích khối nón.
\[972\pi {\mkern 1mu} (c{m^3})\].
\[324\pi (c{m^3})\].
\[324{\mkern 1mu} (c{m^3})\].
\[234\pi {\mkern 1mu} (c{m^3})\].
Cho hình nón có chiều cao \(h = 10cm\) và thể tích \(V = 1000\pi (c{m^3})\). Tính diện tích toàn phần của hình nón.
\[100\pi (c{m^2})\].
\[(300 + 200\sqrt 3 )\pi {\mkern 1mu} (c{m^2})\].
\[300\pi (c{m^2})\].
\[250\pi {\mkern 1mu} (c{m^2})\].
Cho hình nón có chiều cao \(h = 24cm\) và thể tích \[V = 800\pi (c{m^3})\]. Tính diện tích toàn phần của hình nón.
\[160\pi (c{m^2})\].
\[260\pi {\mkern 1mu} (c{m^2})\].
\[300\pi {\mkern 1mu} (c{m^2})\].
\[360\pi {\mkern 1mu} (c{m^2})\].
Cho tam giác vuông \(ABC\) tại \(A\) có \(BC = 20cm;AC = 12cm\). Quay tam giác \(ABC\) cạnh \(AB\) ta được một hình nón có thể tích là:
\[2304{\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[1024\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[786\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[768\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
Cho tam giác vuông \(ABC\) tại \(A\) có \(BC = 10cm;AC = 8cm\). Quay tam giác \(ABC\) cạnh \(AB\) ta được một hình nón có thể tích là:
\[182{\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[128\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\].
\[96\pi {\mkern 1mu} (c{m^3})\].
\[128{\mkern 1mu} {\mkern 1mu} (c{m^3})\].
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh hình nón đó.
Tăng \[4\] lần.
Giảm \[4\] lần.
Tăng \[2\] lần.
Không đổi.
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên ba lần thì diện tích xung quanh hình nón đó.
Tăng \[3\] lần.
Giảm \[3\] lần.
Tăng \[9\] lần.
Không đổi.
Cho tam giác \(ABC\) đều cạnh \(a\), đường trung tuyến \(AM\). Quay tam giác \(ABC\) quanh cạnh \(AM\). Tính diện tích toàn phần của hình nón tạo thành.
\[\frac{{3\pi {a^2}}}{2}\].
\[\frac{{3\pi {a^2}}}{4}\].
\[\frac{{3\pi {a^2}}}{2}\].
\[\frac{{\pi {a^2}}}{2}\].
Cho tam giác \(ABC\) đều cạnh \(4cm\), đường trung tuyến \(AM\). Quay tam giác \(ABC\) quanh cạnh \(AM\). Tính diện tích toàn phần của hình nón tạo thành (đơn vị \(c{m^2}\)).
\[18\pi (c{m^2})\].
\[12(c{m^2})\].
\[12\pi (c{m^2})\].
\[24\pi (c{m^2})\].
Từ một khúc gỗ hình trụ cao \[15{\mkern 1mu} cm\], người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là \[640\pi {\mkern 1mu} {\mkern 1mu} c{m^3}\]. Tính thể tích của khúc gỗ hình trụ.
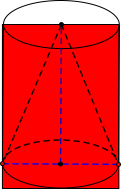
\[960\pi {\mkern 1mu} (c{m^3})\].
\[320\pi {\mkern 1mu} (c{m^3})\].
\[640\pi {\mkern 1mu} (c{m^3})\].
\[690\pi {\mkern 1mu} (c{m^3})\].
Từ một khúc gỗ hình trụ cao \[15{\mkern 1mu} cm\], người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là \[640\pi {\mkern 1mu} {\mkern 1mu} c{m^3}\]. Tính diện tích xung quanh của hình nón.
\[136\pi (c{m^2})\].
\[120\pi {\mkern 1mu} (c{m^2})\].
\[272\pi {\mkern 1mu} (c{m^2})\].
\[163\pi {\mkern 1mu} (c{m^2})\].
Từ một khúc gỗ hình trụ cao \[24{\mkern 1mu} cm\], người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là \[960\pi {\mkern 1mu} {\mkern 1mu} c{m^3}\]. Tính thể tích của khúc gỗ hình trụ.
\[960\pi (c{m^3})\].
\[720\pi {\mkern 1mu} (c{m^3})\].
\[1920\pi {\mkern 1mu} (c{m^3})\].
\[1440\pi {\mkern 1mu} (c{m^3})\].
Từ một khúc gỗ hình trụ cao \[24{\mkern 1mu} cm\], người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là \[960\pi {\mkern 1mu} {\mkern 1mu} c{m^3}\]. Tính diện tích xung quanh của hình nón.
\[4\pi {\mkern 1mu} (c{m^2})\].
\[4\sqrt {2385} {\mkern 1mu} (c{m^2})\].
\[4\sqrt {2385} \pi {\mkern 1mu} (c{m^2})\].
\[2385\pi {\mkern 1mu} (c{m^2})\].
Một hình nón có thể tích bằng \(24\pi \,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\), chiều cao bằng \(2{\rm{dm}}\). Bán kính đáy của hình nón đó bằng
\[6{\rm{dm}}\].
\[\sqrt {24} {\rm{dm}}\].
\[12{\rm{dm}}\].
\[4{\rm{dm}}\].
Một hình nón có diện tích xung quanh gấp đôi diện tích đáy. Thể tích của hình nón đó tính theo bán kính đáy \[r\] là
\(\frac{1}{3}\pi {r^3}\).
\(\frac{2}{3}\pi {r^3}\).
\(\sqrt 3 \pi {r^3}\).
\(\frac{{\sqrt 3 }}{3}\pi {r^3}\).
Cho hình cầu có đường kính \(d = 6cm\). Diện tích mặt cầu là.
\[36\pi \,(c{m^2})\].
\[9\pi {\mkern 1mu} (c{m^2})\].
\[12\pi {\mkern 1mu} (c{m^2})\].
\[36\pi {\mkern 1mu} (cm)\].
Cho mặt cầu có thể tích \(V = 288\pi (c{m^3})\). Tính đường kính mặt cầu.
\[6{\mkern 1mu} cm\].
\[12{\mkern 1mu} cm\].
\[8{\mkern 1mu} cm\].
\[16{\mkern 1mu} cm\].
Cho mặt cầu có thể tích \(V = 972\pi (c{m^3})\). Tính đường kính mặt cầu.
\[18{\mkern 1mu} cm\].
\[12{\mkern 1mu} cm\].
\[9{\mkern 1mu} cm\].
\[16{\mkern 1mu} cm\].
Cho mặt cầu có số đo diện tích bằng với số đo thể tích. Tính bán kính mặt cầu.
\(3\).
\(6\).
\(9\).
\(12\).
Cho mặt cầu có số đo diện tích bằng hai lần với số đo thể tích. Tính bán kính mặt cầu.
\(3\).
\(6\).
\(9\).
\(\frac{3}{2}\).
Cho mặt cầu có bán kính \(3cm\). Một hình nón cũng có bán kính đáy bằng \(3cm\) và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón.
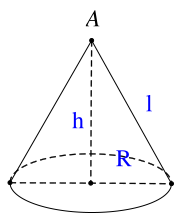
\(3\).
\[6\sqrt 3 \].
\[72\].
\[6\sqrt 2 \].
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu). Tính tỉ số giữa diện tích mặt cầu và diện tích xung quanh của hình trụ.
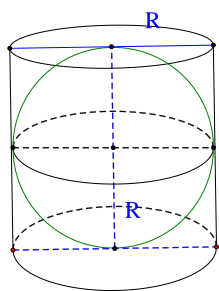
\(3\).
\(1\).
\(\frac{1}{2}\).
\(2\).
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu). Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình trụ.
\[\frac{3}{2}\].
\(1\).
\[\frac{2}{3}\].
\(2\).
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu). Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.
\[\frac{2}{3}\].
\[\frac{3}{2}\].
\(\frac{1}{2}\).
\(2\).
Cho một hình cầu nội tiếp trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy và bán kính đáy của hình trụ bằng bán kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.
\[\frac{4}{3}\].
\[\frac{4}{9}\].
\[\frac{9}{4}\].
\[2\].
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình lập phương.
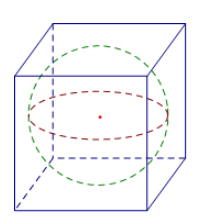
\[\frac{6}{\pi }\].
\[\frac{1}{6}\].
\[\frac{\pi }{6}\].
\[\frac{1}{3}\].
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Nếu diện tích toàn phần của hình lập phương là \[24c{m^2}\] thì diện tích mặt cầu là:
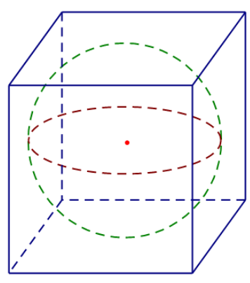
\[4\pi \].
\(4\).
\(2\pi \).
\(2\).
Một hình cầu có số đo thể tích (tính bằng ) gấp đôi số đo diện tích bề mặt (tính bằng ) Bán kính của hình cầu đó bằng
\[6cm\].
\[3cm\].
\[8cm\].
\[12cm\].
Một hình nón có đường sinh bằng \(5cm\), bán kính đáy bằng bán kính của một hình cầu. Diện tích toàn phần hình nón bằng \(\frac{2}{3}\) diện tích hình cầu. Bán kính hình cầu bằng
\(1cm\).
\(\frac{{15}}{8}cm\).
\(3cm\).
\(15cm\).
Gợi ý cho bạn
Xem tất cả54 bài tập Một số yếu tố xác suất có lời giải
39 bài tập Tứ giác nội tiếp có lời giải
35 bài tập Đa giác đều. Phép quay có lời giải
90 bài tập Một số yếu tố thống kê có lời giải
48 bài tập Giải bài toán bằng cách lập phương trình có lời giải