30 câu hỏi
Hình chóp tam giác đều SABC có AB = a, (SC;(ABC)) = 60. Tính thể tích V của SABC
V =
V =
V =
V =
Lăng trụ tam giác đều ABCA’B’C’ có tất cả các cạnh bằng a. Tính diện tích S của A'BC.
S =
S =
S =
S =
Hình chóp SABC có ASB đều cạnh a, (SBC)(ABC). Tính khoảng cách h từ S xuống mp (ABC).
h =
h =
h =
h =
Gọi V là thể tích hình hộp ABCD.A’B’C’D’ và V0 là thể tích của phần hình hộp nằm ở giữa 2 mặt phẳng (A’BD) và (B’CD’). Tính k =
k =
k =
k =
k =
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính khoảng cách từ h giữa BD và SC.
h =
h =
h =
h =
Cho hình lập phương ABCDA’B’C’D’. Tính góc giữa (A’B’C’) và (A’CD’).
= 30
= 45
= 60
= 90
Hình hộp chữ nhật ABCD.A'B'C'D' có thể tích V bằng bao nhiêu nếu biết thể tích tứ diện AB'CD' bằng ?
2
3
Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a có diện tích là:
S =
S =
S =
S =
Hình chóp SABC có SA(ABC), tam giác ABC đều có cạnh 2a, SA = a. Tính khoảng cách h từ điểm A tới mặt phẳng (SBC).
h = a
h = a
h = a
h = a
Tam giác SAC vuông cân tại S và tam giác đều ABC cạnh a được đặt trên hai mặt phẳng vuông góc. Tính khoảng cách h từ SB đến SC.
h =
h =
h =
h =
Hình chóp S.ABC có . Tính thể tích V của SABC.
V =
V =
V =
V =
Tứ diện đều ABCD nội tiếp trong mặt cầu bán kính R. Tính độ dài AB.
AB = R
AB = R
AB = R
AB =
Hình chóp SABCD có đáy ABCD là hình thoi cạnh a với , biết SA(ABCD) và SA = . Tính khoảng cách h từ A tới mặt phẳng (SBC).
h =
h =
h =
h =
Hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích V của hình chóp đó.
V =
V =
V =
V =
Hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp.
R = a
R =
R =
R =
Tính diện tích xung quanh (S) của một khối đa diện lồi có 12 đỉnh là 12 trung điểm các cạnh của một hình lập phương cạnh a.
S =
S =
S =
S =
Khối đa diện lồi có thể tích V1 có 6 đỉnh là giao hai đường chéo của mỗi mặt của một hình hộp có thể tích V. Tính tỉ số k =
k =
k =
k =
k =
Hình chóp SABC có SA(ABC). Hạ AE BC, biết AE = a ; góc giữa (ABC) và (ABC) bằng 60º. Tính khoảng cách h từ A tới mặt phẳng (SBC).
h = a
h =
h =
h =
Hình chóp SABC có SAB và SBC là các tam giác đều cạnh a; SAC là tam giác vuông. Tính thể tích V của hình chóp SABC
V =
V =
V =
V =
Tứ diện đều ABCD nội tiếp trong mặt cầu bán kính R. Tính AB theo R
AB = R
AB = R
AB =
AB =
Cho hình thang vuông ABCD như hình vẽ. Người ta quay hình thang này xung quanh trục CD tạo thành 1 khối tròng xoay có thể tích V. Tính V theo a.
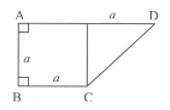
V =
V =
V =
V =
Hình chóp SABCD có đáy ABCD là hình chữ nhật có AD = 2a. SA = SB = a;
(SAD)(ABCD). Tính thể tích V của hình chóp.
V =
V =
V =
V =
Hình lập phương ABCD.A’B’C’D’ có khoảng cách từ A tới mp(A’BD) bằng a. Tính VAB’C’D’
V =
V =
V =
V =
Lăng trụ tam giác ABC.A’B’C’ có DABC đều cạnh a, AA’ = a, . Tính thể tích lăng trụ.
V =
V =
V =
V =
Cho 3 tia Ox, Oy, Oz đôi một tạo với nhau góc 60°. Trên tia Ox lấy điểm A sao cho OA = a. Tính khoảng cách (A, (Oyz))?
h =
h =
h =
h =
Cho hình thang ABCD (AB = BC = CD = a, AD = 2a) quay quanh BC tạo thành khối tròn xoay có thể tích V. Tính V.
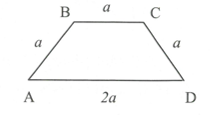
V =
V =
V =
V =
Hình chóp S.ABCD đáy ABCD là hình thang vuông tại A, B; SA ^ (ABCD) với SA = AB = BC = a, AD = 2a. Tính khoảng cách h giữa AC, SD.
h = a
h =
h =
h =
Hình chóp S.ABC có SA = a, SB = a, SC = a, . Tính khoảng cách h từ A tới mp(SBC).
h = a
Mặt phẳng (P) thay đổi luôn đi qua M (1; 2; 3). Biết (P) cắt các tia Ox, Oy, Oz tại A, B, C. Tìm GTNN của thể tích OABC (Vmin).
Vmin = 24.
Vmin = 27.
Vmin =
Vmin = 36.
Hình chóp tứ giác đều SABCD có AB = a; góc (SC, (ABCD) = 30°. Tính khoảng cách h từ điểm S đến (ABCD)
h = a
h = a
h =
h =







