Quiz

333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết (P6)

VietJackToánLớp 123 lượt thi

30 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 $°$ Gọi M, N lần lượt là trung điểm của các cạnh SD, DC. Thể tích khối tứ diện ACMN là

$\frac{a^{3}}{8}$

$\frac{a^{3} \sqrt{2}}{2}$

$\frac{a^{3} \sqrt{3}}{6}$

$\frac{a^{3} \sqrt{2}}{4}$

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, SA = a $\sqrt{3}$ , cạnh bên SA vuông góc với đáy. Thể tích của khối chóp S.ABC bằng

$\frac{a^{3} \sqrt{3}}{2}$

$\frac{a^{3}}{2}$

$\frac{a^{3} \sqrt{3}}{4}$

$\frac{a^{3}}{4}$

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối chóp S.ABCD cạnh bên SA vuông góc với đáy, đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA = 3a. Thể tích của khối chóp S.ABCD bằng

6 $a^{3}$

$\frac{a^{3}}{3}$

2 $a^{3}$

$a^{3}$

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình bát diện đều có số cạnh là

10.

12.

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối lập phương ABCD.A'B'C'D'. Mặt phẳng (BDD'B') chia khối lập phương thành

Hai khối lăng trụ tam giác.

Hai khối tứ diện.

Hai khối lăng trụ tứ giác.

Hai khối chóp tứ giác.

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và đáy bằng 30 $°$ . Thể tích khối chóp S.ABC bằng:

$\frac{a^{3} \sqrt{2}}{18}$

$\frac{a^{3} \sqrt{2}}{36}$

$\frac{a^{3} \sqrt{3}}{18}$

$\frac{a^{3} \sqrt{3}}{36}$

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường cao SO. Biết SO = $\frac{a \sqrt{2}}{2}$ thể tích khối chóp S.ABCD bằng:

$\frac{a^{3} \sqrt{2}}{6}$

$\frac{a^{3} \sqrt{2}}{3}$

$\frac{a^{3} \sqrt{2}}{2}$

$\frac{a^{3} \sqrt{3}}{4}$

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

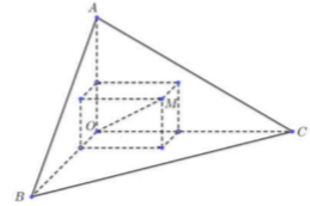
Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = 3cm, OB = 6cm, OC = 12cm. Trên mặt (ABC) người ta đánh dấu một điểm M sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện (xem hình vẽ).

Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng:

8 $c m^{3}$

24 $c m^{3}$

12 $c m^{3}$

36 $c m^{3}$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối chóp tam giác S.ABC có cạnh bên SA vuông góc với mặt phẳng (ABC), đáy là tam giác ABC cân tại A, độ dài trung tuyến AD bằng a, cạnh bên SB tạo với đáy góc và tạo với mặt phẳng (SAD) góc 30 $°$ . Thể tích khối chóp S.ABC bằng

$\frac{a^{3}}{3}$

$\frac{a^{3} \sqrt{3}}{3}$

$\frac{a^{3} \sqrt{3}}{6}$

$\frac{a^{3}}{6}$

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho lăng trụ đều ABC.A'B'C'. Biết rằng góc giữa (A'BC) và (ABC) là 30 $°$ , tam giác A'BC có diện tích bằng 2. Thể tích khối lăng trụ ABC.A'B'C' bằng

$2 \sqrt{6}$

$\frac{\sqrt{6}}{2}$

$\sqrt{3}$

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện đều ABCD. Góc giữa hai đường thằng AB và CD là

60 $°$

90 $°$

45 $°$

30 $°$

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho một hình chóp tam giác đều có cạnh bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 $°$ . Thể tích khối chóp đó là

$\frac{a^{3} \sqrt{3}}{12}$

$\frac{a^{3} \sqrt{3}}{36}$

$\frac{a^{3}}{12}$

$\frac{a^{3}}{36}$

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt phẳng đáy, biết AB = 4a, SB = 6a. Tính thể tích khối chóp S.ABC là V. Tính tỉ số $\frac{4 a^{3}}{3 V}$ có giá trị là

$\frac{\sqrt{5}}{10}$

$\frac{3 \sqrt{5}}{8}$

$\frac{\sqrt{5}}{8}$

$\frac{\sqrt{5}}{160}$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Thể tích của khôi lăng trụ đứng tam giác đều có tất cả các cạnh bằng a bằng

$\frac{a^{3} \sqrt{3}}{2}$

$\frac{a^{3}}{3}$

$\frac{a^{3} \sqrt{3}}{4}$

$\frac{a^{3} \sqrt{3}}{6}$

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a, mặt bên tạo với đáy một góc 60 $°$ . Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng

$\frac{a \sqrt{3}}{2}$

$\frac{a \sqrt{2}}{2}$

$a \sqrt{3}$

$\frac{3 a}{4}$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N theo thứ là trung điểm của SA, SB. Tỉ số thể tích $\frac{V_{S . C D M N}}{V_{S . C D A B}}$ là

$\frac{5}{8}$

$\frac{3}{8}$

$\frac{1}{4}$

$\frac{1}{2}$

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình lăng trụ có thể có số cạnh là số nào sau đây?

3000.

3001.

3005.

3007.

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Một hình hộp chữ nhật (không phải hình lập phương) có bao nhiêu mặt phẳng đối xứng?

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' bằng BC bằng $\frac{a \sqrt{3}}{4}$ . Tính theo thể tích của khối lăng trụ ABC.A'B'C'.

V = $\frac{a^{3} \sqrt{3}}{24}$

V = $\frac{a^{3} \sqrt{3}}{12}$

V = $\frac{a^{3} \sqrt{3}}{6}$

V = $\frac{a^{3} \sqrt{3}}{3}$

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối lăng trụ ABC.A'B'C' có thể tích bằng V. Tính thể tích khối đa diện ABC.A'B'C' theo V.

$\frac{3 V}{4}$

$\frac{2 V}{3}$

$\frac{V}{2}$

$\frac{V}{4}$

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Cosin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều có tất cả các cạnh bằng nhau là

$\frac{1}{3}$

$\frac{1}{\sqrt{3}}$

$\frac{\sqrt{3}}{2}$

$\frac{1}{\sqrt{2}}$

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho lăng trụ tam giác ABC.A'B'C', biết thể tích lăng trụ là V. Tính thể tích khối chóp C.ABB'A'?

$\frac{2}{3}$ V

$\frac{1}{3}$ V

$\frac{3}{4}$ V

$\frac{1}{2}$ V

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết $V_{S . A B C D} = \frac{a^{3}}{3 \sqrt{3}}$ . Tính góc giữa SA và mặt phẳng (SCD).

60 $°$

45 $°$

30 $°$

90 $°$

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Tính thể tích của khối bát diện đều có tất cả các cạnh bằng 2a.

$\frac{\sqrt{2}}{6} a^{3}$

$\frac{4 \sqrt{2}}{3} a^{3}$

$\frac{8 \sqrt{2}}{3} a^{3}$

$\frac{2 \sqrt{2}}{3} a^{3}$

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

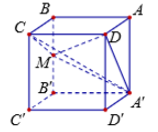
Cho hình lập phương ABCD.A'B'C'D' có tất cả các cạnh bằng 1. Gọi M là trung điểm của BB'. Tính thể tích khối A'MCD.

$\frac{1}{12}$

$\frac{2}{15}$

$\frac{4}{15}$

$\frac{1}{28}$

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC).

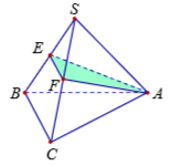
Thể tích của khối chóp S.ABC.

$\frac{a^{3} \sqrt{5}}{8}$

$\frac{a^{3} \sqrt{5}}{24}$

$\frac{a^{3} \sqrt{6}}{12}$

$\frac{a^{3} \sqrt{3}}{24}$

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABC có AB = a, $\hat{A S B} = 30 °$ . Lấy các điểm B', C' lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tính chu vi đó.

( $\sqrt{3}$ -1)a

$\sqrt{3}$ a

$\frac{a}{\sqrt{3} + 1}$

(1+ $\sqrt{3}$ )a

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp tứ giác đều có tất cả các cạnh bằng a. Côsin của góc giữa mặt bên và mặt đáy bằng:

$\frac{1}{\sqrt{3}}$

$\frac{1}{3}$

$\frac{1}{2}$

$\frac{1}{\sqrt{2}}$

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tam giác SAD vuông tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết AB = a, SA = 2SD, mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 60 $°$ . Thể tích của khối chóp S.ABCD bằng:

$\frac{15 a^{3}}{2}$

$\frac{3 a^{3}}{2}$

$\frac{5 a^{3}}{2}$

$5 a^{3}$

Xem đáp án

30. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABCD có AC = 2a, góc giữa mặt phẳng (SBC) và mặt đáy bằng 45 $°$ . Thể tích của khối chóp S.ABCD bằng:

$a^{3} \sqrt{2}$ .

$\frac{2 \sqrt{3} a^{3}}{3}$ .

$\frac{a^{3} \sqrt{2}}{3}$ .

$\frac{a^{3}}{2}$ .