Quiz

333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết (P7)

Admin30 câu hỏiToánLớp 12

30 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a $\sqrt{3}$ . Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:

A. arcsin $\frac{\sqrt{3}}{5}$

B. 45 $°$

C. 60 $°$

D. 30 $°$

2. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SB vuông góc với mặt phẳng đáy. Biết SB = 3a, AB = 4a, BC = 2a. Khoảng cách từ B đến mặt phẳng (SAC) bằng:

A. $\frac{12 \sqrt{61} a}{61}$

B. $\frac{3 \sqrt{14} a}{14}$

C. $\frac{4 a}{5}$

D. $\frac{12 \sqrt{29} a}{29}$

3. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA $⊥$ (ABCD). Gọi M là hình chiếu của A trên SB. Khẳng định nào sau đây đúng?

A. AM $⊥$ SD

B. AM $⊥$ (SCD)

C. AM $⊥$ CD

D. AM $⊥$ (SBC)

4. Nhiều lựa chọn

Cho khối chóp tứ giác đều S.ABCD. Gọi M là trung điểm SC, mặt phẳng (P) chứa AM và song song với BD chia khối chóp thành 2 khối đa diện. Đặt $V_{1}$ là thể tích khối đa diện có chứa đỉnh S và $V_{2}$ là thể tích khối đa diện có chứa đáy. Tỉ số $\frac{V_{1}}{V_{2}}$ bằng:

A. $\frac{V_{1}}{V_{2}}$ = $\frac{3}{2}$

B. $\frac{V_{1}}{V_{2}}$ = $\frac{1}{2}$

C. $\frac{V_{1}}{V_{2}}$ = $\frac{2}{3}$

D. $\frac{V_{1}}{V_{2}}$ = 1

5. Nhiều lựa chọn

Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết SC = a $\sqrt{3}$ ?

A. $\frac{2 a^{3} \sqrt{6}}{9}$

B. $\frac{a^{3} \sqrt{6}}{12}$

C. $\frac{a^{3} \sqrt{3}}{4}$

D. $\frac{a^{3} \sqrt{3}}{12}$

6. Nhiều lựa chọn

Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất

A. Bốn cạnh

B. Năm cạnh

C. Hai cạnh

D. Ba cạnh

7. Nhiều lựa chọn

Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa hai mặt bên không liền kề nhau.

A. $\frac{1}{3}$

B. $\frac{1}{\sqrt{2}}$

C. $\frac{1}{2}$

D. $\frac{5}{3}$

8. Nhiều lựa chọn

Cho hình chóp có đáy là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA = 2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng là trung điểm của H của đoạn thẳng AO. Tính khoảng cách d giữa các đường thẳng SD và AB.

A. d = 4a.

B. d = $\frac{4 a \sqrt{22}}{11}$

C. d = 2a

D. d = $\frac{3 a \sqrt{2}}{11}$

9. Nhiều lựa chọn

Cho hình chóp đều có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60 $°$ . Tính theo thể tích khối chóp S.ABC.

A. V = $\frac{a^{3} \sqrt{3}}{24}$

B. V = $\frac{a^{3}}{8}$

C. V = $\frac{a^{3} \sqrt{3}}{12}$

D. V = $\frac{a^{3} \sqrt{3}}{8}$

10. Nhiều lựa chọn

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, BC = a, mặt phẳng (A'BC) tạo với đáy một góc 30 $°$ và tam giác có diện tích bằng $a^{2} \sqrt{3}$ . Tính thể tích khối lăng trụ ABC.A'B'C'.

A. $\frac{3 a^{3} \sqrt{3}}{2}$

B. $\frac{3 a^{3} \sqrt{3}}{8}$

C. $\frac{a^{3} \sqrt{3}}{8}$

D. $\frac{3 a^{3} \sqrt{3}}{4}$

11. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2 $a^{2}$ , AB = a $\sqrt{2}$ ; BC = 2a. Gọi M là trung điểm của DC. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng

A. $\frac{4 a \sqrt{10}}{15}$

B. $\frac{3 a \sqrt{10}}{5}$

C. $\frac{2 a \sqrt{10}}{5}$

D. $\frac{3 a \sqrt{10}}{15}$

12. Nhiều lựa chọn

Cho khối chóp S.ABCD có đáy là hình bình hành, gọi B' và D' theo thứ tự là trung điểm các cạnh SB, SD. Mặt phẳng (AB'D') cắt cạnh SC tại C’. Tính tỷ số thể tích của hai khối đa diện được chia ra bởi mặt phẳng (AB'D')

A. $\frac{1}{2}$

B. $\frac{1}{6}$

C. $\frac{1}{12}$

D. $\frac{1}{5}$

13. Nhiều lựa chọn

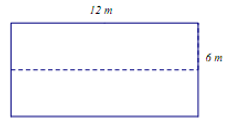
Trong một đợt tổ chức cho học sinh tham gia dã ngoại ngoài trời. Để có thể có chỗ nghỉ ngơi trong quá trình tham quan dã ngoại, các bạn học sinh đã dựng trên mặt đất bằng phẳng 1 chiếc lều bằng bạt từ một tấm bạt hình chữ nhật có chiều dài là 12m và chiều rộng là 6m bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau x (m) (xem hình vẽ). Tìm x để khoảng không gian phía trong lều là lớn nhất?

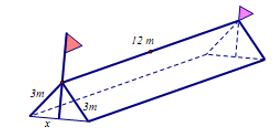
A. x = $3 \sqrt{3}$

B. x = $3 \sqrt{2}$

C. x = 2

D. x = 4

14. Nhiều lựa chọn

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA $⊥$ (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Tính $\frac{50 V \sqrt{3}}{a^{3}}$ , với V là thể tích khối chóp A.BCMN

A. 10

B. 12

C. 9

D. 11

15. Nhiều lựa chọn

Cho tứ diện S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết SA = 3a, SB = 4a, SC = 5a. Tính theo a thể tích V của khối tứ diện S.ABC

A. V = 20 $a^{3}$

B. V = 10 $a^{3}$

C. $\frac{5 a^{3}}{2}$

D. 5 $a^{3}$

16. Nhiều lựa chọn

Cho hình chóp SABC có A', B' lần lượt là trung điểm của SA, SB. Gọi $V_{1}, V_{2}$ lần lượt là thể tích của khối chóp SA'B'C và SABC. Tính tỉ số $\frac{V_{1}}{V_{2}}$

A. $\frac{1}{8}$

B. $\frac{1}{4}$

C. $\frac{1}{2}$

D. $\frac{1}{3}$

17. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD), SA = 2a. Tính theo a thể tích khối chóp S.ABC

A. $\frac{a^{3}}{3}$

B. $\frac{a^{3}}{6}$

C. $\frac{a^{3}}{4}$

D. $\frac{a^{3}}{5}$

18. Nhiều lựa chọn

Cho tam giác có A(1;-1), B(3;-3), C(6;0). Diện tích $∆$ ABC là

A. 6

B. 6 $\sqrt{2}$

C. 12

D. 8

19. Nhiều lựa chọn

Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt là hình vuông cạnh a. Các điểm M, N lần lượt nằm trên AD', DB sao cho AM = DN = x; (0 < x < a $\sqrt{2}$ ). Khi x thay đổi, đường thẳng MN luôn song song với mặt phẳng cố định nào sau đây?

A. (CB'D')

B. (A'BC)

C. (AD'C)

20. Nhiều lựa chọn

Cho khối hộp ABCD.A'B'C'D' có thể tích bằng 2018. Gọi M là trung điểm của cạnh AB. Mặt phẳng (MB'D') chia khối chóp ABCD.A'B'C'D' thành hai khối đa diện. Tính thể tích phần khối đa diện chứa đỉnh A

A. $\frac{5045}{6}$

B. $\frac{7063}{6}$

C. $\frac{10090}{17}$

D. $\frac{7063}{12}$

21. Nhiều lựa chọn

Cho lăng trụ tam giác ABC.A'B'C'. Đặt $\vec{A A'} = \vec{a}, \vec{A B} = \vec{b}, \vec{A C} = \vec{c}$ . Gọi I là điểm thuộc CC' sao cho $\vec{C' I} = \frac{1}{3} \vec{C' C}$ , điểm G thỏa mãn $\vec{G B} + \vec{G A'} + \vec{G B'} + \vec{G C'} = \vec{0}$ . Biểu diễn véc tơ $\vec{I G}$ qua véc tơ $\vec{a}, \vec{b}, \vec{c}$ . Trong các khẳng định sau, khẳng định nào là khẳng định đúng?

A. $\vec{I G} = \frac{1}{4} (\frac{1}{3} \vec{a} + 2 \vec{b} - 3 \vec{c})$

B. $\vec{I G} = \frac{1}{3} (\frac{1}{3} \vec{a} + \vec{b} + 2 \vec{c})$

C. $\vec{I G} = \frac{1}{4} (\vec{a} + \vec{b} - 2 \vec{c})$

D. $\vec{I G} = \frac{1}{4} (\vec{a} + \frac{1}{3} \vec{b} - 2 \vec{c})$

22. Nhiều lựa chọn

Cho hình chóp S.ABC có SA = 1, SB = 2, SC = 3 và $\hat{A S B} = 60 °, \hat{B S C} = 120 °, \hat{C S A} = 90 °$ . Tính thể tích khối chóp S.ABC.

A. $\frac{\sqrt{2}}{2}$

B. $\sqrt{2}$

C. $\frac{\sqrt{2}}{6}$

23. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a. Biết SA vuông góc với đáy (ABCD) và SA = a. Gọi M, N lần lượt là trung điểm SB, CD. Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC).

A. $\frac{\sqrt{5}}{5}$

B. $\frac{\sqrt{55}}{10}$

C. $\frac{3 \sqrt{5}}{10}$

24. Nhiều lựa chọn

Hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AA' = a $\sqrt{2}$ . Tính thể tích V của A'BB'D.

A. V = $\frac{a^{3} \sqrt{3}}{2}$

B. V = $\frac{2 a^{3} \sqrt{2}}{3}$

C. V = $a^{3} \sqrt{2}$

D. V = $\frac{a^{3} \sqrt{2}}{3}$

25. Nhiều lựa chọn

Hình chóp SABC có $∆$ SAB, $∆$ SBC là các tam giác đều cạnh a, mp(SAC) $⊥$ mp(ABC). Tính AC.

A. AC = 2a.

B. AC = a $\sqrt{3}$ .

C. AC = a $\sqrt{2}$ .

D. AC = a.

26. Nhiều lựa chọn

Cho tứ diện ABCD. M thuộc đoạn AB và AM = $\frac{1}{3}$ AB. Gọi ( $α$ ) là mặt phẳng qua M, ( $α$ )// AC, ( $α$ )// BD. Gọi $V_{1}, V_{2}$ là 2 phần thể tích tứ diện được chia ra bởi ( $α$ ). Tính k = $\frac{V_{1}}{V_{2}}$ (V₁ là thể tích đa diện có chứa đỉnh A).

A. k = $\frac{5}{9}$

B. k = $\frac{1}{3}$

C. k = $\frac{12}{15}$

D. k = $\frac{7}{20}$

27. Nhiều lựa chọn

Cho lục giác đều ABCDEF cạnh a. Cho tứ giác ABCD quay quanh AD tạo thành khối tròn xoay có thể tích V. Tính V.

A. V = $\frac{3 {πa}^{3} \sqrt{3}}{4}$

B. V = ${πa}^{3}$

C. V = ${πa}^{3}$ $\sqrt{2}$

D. V = $\frac{7 {πa}^{3}}{8 \sqrt{3}}$

28. Nhiều lựa chọn

Hình chóp SABCD, đáy ABCD là hình thoi, $∆$ BCD là $∆$ đều cạnh a, tâm H. Biết SH $⊥$ (ABCD) và $∆$ SAC vuông tại S. Tính thể tích V của SABCD.

A. V = $\frac{a^{3} \sqrt{3}}{4}$

B. V = $\frac{a^{3} \sqrt{2}}{6}$

C. V = $\frac{a^{3} \sqrt{3}}{3}$

D. V = $\frac{a^{3}}{3}$

29. Nhiều lựa chọn

Hình hộp chữ nhật ABCDA’B’C’D’ có AB = a, AD = a $\sqrt{2}$ và khoảng cách (D,(AD'C)) = $\frac{\sqrt{2} a}{3}$ . Tính AA’.

A. AA' = $\frac{a}{\sqrt{3}}$

B. AA' = $a \sqrt{3}$

C. AA' = a

D. AA' = $\frac{a}{\sqrt{3}}$

30. Nhiều lựa chọn

Cho lăng trụ tam giác đều ABCA’B’C’ có AA' = $\frac{a}{2}, ∆$ ABC đều cạnh a. Tính diện tích S của $∆$ A'BC.

A. S = $\frac{a^{2} \sqrt{3}}{4}$

B. S = $\frac{a^{3} \sqrt{3}}{2}$

C. S = $\frac{a^{2} \sqrt{2}}{2}$

D. S = $\frac{a^{2}}{2}$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi2 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi4 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi27 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi15 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi12 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi12 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi12 lượt thi

Facebook Youtube