Quiz

333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết (P3)

VietJackToánLớp 122 lượt thi

Xem trước Bắt đầu ngay

30 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Số đỉnh của hình bát diện đều là:

10.

12.

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?

1 mặt phẳng.

2 mặt phẳng.

3 mặt phẳng.

4 mặt phẳng.

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và góc $\hat{(S D, (A B C D))} = 60 °$ . Gọi a là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính tana

tana = $\frac{4 \sqrt{15}}{9}$

tana = $\frac{\sqrt{30}}{12}$

tana = $\frac{\sqrt{10}}{3}$

tana = $\frac{\sqrt{30}}{3}$

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, có SA vuông góc với mặt phẳng (ABCD). Biết SC = a $\sqrt{3}$ khoảng cách giữa BD và SC theo a là:

$\frac{a \sqrt{6}}{6}$

$\frac{a \sqrt{6}}{2}$

$\frac{a \sqrt{6}}{3}$

$a \sqrt{6}$

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, có SA vuông góc với mặt phẳng (ABCD). Biết SC = a $\sqrt{3}$ khoảng cách giữa BD và SC theo a là:

$\frac{a \sqrt{6}}{6}$

$\frac{a \sqrt{6}}{2}$

$\frac{a \sqrt{6}}{3}$

$a \sqrt{6}$

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB = a $\sqrt{2}$ . Biết SA $⊥$ (ABC) và SA = a. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng:

30^o.

45^o.

60^o.

90^o.

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho đa giác đều $A_{1} A_{2} A_{3} . . . A_{30}$ nội tiếp trong đường tròn (O). Tính số hình chữ nhật có các đỉnh là 4 trong 30 đỉnh của đa giác đó.

105.

27405.

27406.

106.

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào sau đây là đúng?

S = $4 \sqrt{3} a^{2}$

S = $\sqrt{3} a^{2}$

S = $2 \sqrt{3} a^{2}$

S = $8 a^{2}$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong không gian cho tứ diện ABCD có I, J là trọng tâm các tam giác ABC, ABD. Khẳng định nào sau đây là đúng?

IJ//(BCD)

IJ//(ABC)

IJ//(BIJ)

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hình dưới đây, hình nào không phải đa diện lồi

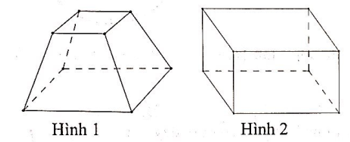
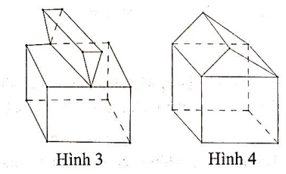
Hình 1

Hình 2

Hình 3

Hình 4

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ đứng ABC.A'B'C' có đáy tam giác ABC vuông, AB = BC = 2a, cạnh bên AA' = a $\sqrt{2}$ là trung điểm của BC. Tính tan của góc giữa A'M với (ABC).

$\frac{\sqrt{10}}{5}$

$\frac{2 \sqrt{2}}{3}$

$\frac{\sqrt{3}}{3}$

$\frac{2 \sqrt{10}}{5}$

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA = 2a. Gọi M là trung điểm của SC. Tính côsin của góc $α$ là góc giữa đường thẳng BM và mặt phẳng (ABC).

cos $α$ = $\frac{\sqrt{7}}{14}$

cos $α$ = $\frac{2 \sqrt{7}}{7}$

cos $α$ = $\frac{\sqrt{5}}{7}$

cos $α$ = $\frac{\sqrt{2}}{7}$

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có AB = 3. Hình chiếu của S lên mặt phẳng (ABC) là điểm H thuộc miền trong tam giác ABC sao cho $\hat{A H B} = 120 °$ . Tính bán kính R mặt cầu ngoại tiếp hình chóp S.HAB, biết SH = 4 $\sqrt{3}$ .

R = $\sqrt{5}$

R = 3 $\sqrt{5}$

R = $\sqrt{15}$

R = 2 $\sqrt{3}$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích là V. Biết A'M = MA, DN = 3ND', CP = 2PC'. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Tính thể tích khối đa diện nhỏ hơn tính theo V bằng?

$\frac{5 V}{12}$

$\frac{7 V}{12}$

$\frac{V}{4}$

$\frac{V}{6}$

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ ABC.A'B'C' có AA' = $\frac{a \sqrt{10}}{4}$ , AC = a $\sqrt{2}$ , BC = a, $\hat{A C B} = 135 °$ . Hình chiếu vuông góc của C' lên mặt phẳng (ABC) trùng với trung điểm M của AB. Tính góc tạo bởi đường thẳng C'M với mặt phẳng (ACC'A')?

$90 °$

$60 °$

$45 °$

$30 °$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ ABC.A'B'C' có A'.ABC là tứ diện đều cạnh a. Gọi M,N lần lượt là trung điểm của AA' và BB'. Tính tan của góc giữa hai mặt phẳng (ABC) và (CMN).

$\frac{\sqrt{2}}{5}$

$\frac{3 \sqrt{2}}{4}$

$\frac{2 \sqrt{2}}{5}$

$\frac{4 \sqrt{2}}{5}$

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).

h = $\frac{a}{3}$

h = $\frac{a \sqrt{6}}{6}$

h = $\frac{a \sqrt{6}}{3}$

h = $\frac{a \sqrt{3}}{6}$

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a, cạnh bên SA vuông góc với đáy, SA = a $\sqrt{3}$ . Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB).

$\frac{\sqrt{3}}{2}$

$\frac{\sqrt{21}}{7}$

$\frac{2 \sqrt{7}}{7}$

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A’C’, BB’. Thể tích của khối tứ diện CMNP bằng:

$\frac{5}{24}$ V

$\frac{1}{4}$ V

$\frac{7}{24}$ V

$\frac{1}{3}$ V

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình lập phương có bao nhiêu mặt phẳng đối xứng?

4 mặt phẳng

6 mặt phẳng

8 mặt phẳng

9 mặt phẳng

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp tứ giác S.ABCD có tất cả các cạnh bằng a. Gọi M là điểm trên đoạn SD sao cho SM = 2SD. Tan góc giữa đường thẳng BM và mặt phẳng bằng bao nhiêu?

$\frac{1}{3}$

$\frac{\sqrt{5}}{5}$

$\frac{\sqrt{3}}{3}$

$\frac{1}{5}$

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a, mặt bên SAB đều và nằm trong mặt phẳng vuông góc với (ABCD). Khoảng cách từ điểm A đến mặt phẳng (SCD) theo a là:

$\frac{a \sqrt{21}}{21}$

$\frac{a \sqrt{21}}{7}$

$\frac{3 a \sqrt{21}}{7}$

$\frac{a \sqrt{21}}{3}$

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA = a và vuông góc với (ABCD). M, N lần lượt là trung điểm AD, DC. Góc giữa mặt phẳng (SBM) với mặt phẳng (ABCD) bằng $45 °$ . Khoảng cách từ điểm D đến mặt phẳng (SBM) là:

a $\sqrt{2}$

$\frac{a \sqrt{2}}{3}$

$\frac{a \sqrt{2}}{2}$

$\frac{a \sqrt{2}}{6}$

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

Khối mười hai mặt đều có bao nhiêu đỉnh?

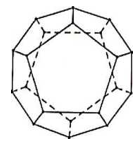
12.

16.

20.

36.

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông tại B. Biết SA = AB = BC. Tính góc giữa đường thẳng SB và mặt phẳng (SAC).

$30 °$

$45 °$

$60 °$

$90 °$

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại S, hình chiếu của S lên mặt phẳng là điểm H thuộc cạnh AD sao cho AH = 3HD. Gọi M là trung điểm của AB, biết SA = 2a $\sqrt{3}$ và đường thẳng SC tạo với đáy một góc 30°. Khoảng cách từ điểm M đến mặt phẳng (SBC) là:

$\frac{2 a \sqrt{66}}{11}$

$\frac{a \sqrt{66}}{22}$

$\frac{a \sqrt{66}}{66}$

$\frac{a \sqrt{66}}{11}$

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện ABCD có AB = 6, CD = 8. Cắt tứ diện bởi một mặt phẳng song song với AB, CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng:

$\frac{31}{7}$

$\frac{18}{7}$

$\frac{24}{7}$

$\frac{15}{7}$

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R = 3cm, góc ở đỉnh hình nón là $φ = 120 °$ . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng: