Quiz

333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết (P2)

VietJackToánLớp 123 lượt thi

30 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện ABCD có (ACD) $⊥$ (BCD), AC = AD = BC = BD = a, CD = 2x . Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là:

$\frac{a \sqrt{2}}{3}$

$\frac{a \sqrt{3}}{3}$

$\frac{a \sqrt{3}}{2}$

$\frac{a \sqrt{5}}{3}$

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AC' = $\sqrt{6}$ a. Thể tích khối hộp chữ nhật ABCD.A'B'C'D' bằng:

$\frac{\sqrt{3} a^{3}}{3}$

$\frac{2 a^{3}}{3}$

$2 a^{3}$

$2 \sqrt{3} a^{3}$

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M , N, P lần lượt là trung điểm các cạnh CD, A'B', A'D' . Thể tích khối tứ diện A' MNP bằng:

$\frac{a^{3}}{16}$

$\frac{a^{3}}{32}$

$\frac{a^{3}}{12}$

$\frac{a^{3}}{24}$

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABC có cạnh đáy bằng a . Gọi M , N lần lượt là trung điểm của SA và SC. Biết rằng BM vuông góc với AN . Thể tích khối chóp S.ABC bằng:

$\frac{\sqrt{14} a^{3}}{8}$

$\frac{\sqrt{3} a^{3}}{4}$

$\frac{\sqrt{3} a^{3}}{12}$

$\frac{\sqrt{14} a^{3}}{24}$

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết SA = 3, SB = 4, SC 5, thể tích khối chóp S.ABC bằng

20.

30.

10.

60.

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đường cao SA tam giác ABC vuông tại A có AB = 2, AC = 4. Gọi H là trung điểm của BC. Biết diện tích tam giác SAH bằng 2, thể tích của khối chóp S.ABC bằng

$\frac{16 \sqrt{5}}{15}$

$\frac{16 \sqrt{5}}{5}$

$\frac{4 \sqrt{5}}{9}$

$\frac{4 \sqrt{5}}{3}$

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác cân tại A có AB = a, $\hat{B A C} = 120^{0}$ . Biết thể tích khối chóp S.ABC bằng $\frac{\sqrt{3} a^{3}}{4}$ góc giữa hai mặt phẳng (SBC) và (ABC) bằng

$90^{0}$

$30^{0}$

$60^{0}$

$45^{0}$

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện ABCD có AB = AC = AD = 2a. Biết tam giác BCD có BC = 2a, BD = a, $\hat{C B D} = 120^{0}$ . Tính thể tích tứ diện ABCD theo a.

$\frac{\sqrt{5}}{3} a^{3}$

$\frac{\sqrt{5}}{2} a^{3}$

$\sqrt{5} a^{3}$

$\frac{\sqrt{5}}{6} a^{3}$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SB và SD lần lượt tại M và N. Gọi $V_{1}$ là thể tích của khối chóp S.AMPN Giá trị nhỏ nhất của tỉ số $\frac{V_{1}}{V}$ bằng

$\frac{1}{3}$

$\frac{1}{8}$

$\frac{2}{3}$

$\frac{3}{8}$

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình hộp ABCD.A'B'C'D' Tính tỉ số thể tích của khối tứ diện BDA'C' và khối hộp ABCD.A'B'C'D'

$\frac{1}{5}$

$\frac{2}{3}$

$\frac{1}{3}$

$\frac{2}{5}$

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và tam giác ABD đều. SO vuông góc mặt phẳng (ABCD) và SO = 2a. M là trung điểm của SD. Tang góc giữa CM và (ABCD) là:

$4 \sqrt{13}$

$\frac{4 \sqrt{13}}{13}$

$\frac{\sqrt{13}}{4}$

$\frac{\sqrt{13}}{13}$

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, $\hat{A B C} = 60^{0}, S A ⊥ (A B C D), S A = \frac{3 a}{2}$ . Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng:

$\frac{3 a}{4}$

$\frac{3 a}{8}$

$\frac{5 a}{8}$

$\frac{5 a}{4}$

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C. Cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC.A'B'C' là:

$a^{3} \sqrt{3}$

$\frac{a^{3} \sqrt{3}}{2}$

$\frac{a^{3} \sqrt{3}}{6}$

$\frac{a^{3} \sqrt{3}}{4}$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình trụ bán kính đáy r. Gọi O và O' là tâm của hai đường tròn đáy với OO' = 2r. Một mặt cầu tiếp xúc với hai đáy của hình trụ lại O và O'. Gọi $V_{C}$ và $V_{T}$ lần lượt là thể tích của khối cầu và khối trụ. Khi đó là

$\frac{1}{2}$

$\frac{3}{4}$

$\frac{2}{3}$

$\frac{3}{5}$

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

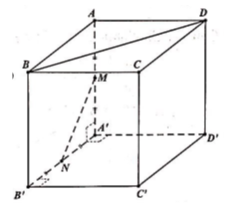
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AA' và A'B'. Số đo góc giữa hai đường thẳng MN và BD (như hình vẽ bên) là:

45°.

30°.

60°.

90°.

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 3a, AD = 2a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AB sao cho AH=2HB. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng 60°. Khoảng cách từ A đến mặt phẳng (SBC) là:

$\frac{2 a \sqrt{39}}{13}$

$\frac{3 a \sqrt{39}}{13}$

$\frac{a \sqrt{39}}{13}$

$\frac{6 a \sqrt{39}}{13}$

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng:

Qua M và song song với AB

Qua N và song song với BD

Qua G và song song với CD

Qua G và song song với BC

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối chóp O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Biết OA = 1, OB = 2 và thể tích khối chóp O.ABC bằng 3. Độ dài cạnh OC bằng:

$\frac{3}{2}$

$\frac{9}{2}$

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD = 2a và AA’ = 3a. Bán kính mặt cầu ngoại tiếp tứ diện ACB’D’ là:

$\frac{a \sqrt{3}}{2}$

$\frac{a \sqrt{3}}{4}$

$\frac{a \sqrt{14}}{2}$

$\frac{a \sqrt{6}}{2}$

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính tang của góc giữa đường thẳng SC và mặt đáy.

$\frac{\sqrt{15}}{5}$

$\frac{\sqrt{15}}{3}$

$\frac{2 \sqrt{5}}{5}$

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N là trung điểm của SC, SD. Tính cosin của góc giữa hai mặt phẳng (GMN) và (ABCD).

$\frac{2 \sqrt{39}}{39}$

$\frac{\sqrt{3}}{6}$

$\frac{2 \sqrt{39}}{13}$

$\frac{\sqrt{13}}{13}$

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

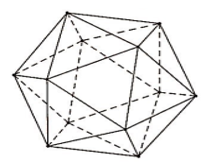
Khối 20 mặt đều như hình vẽ bên có bao nhiêu đỉnh?

10.

12.

16.

20.

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng đáy là điểm H thuộc cạnh BC sao cho $\vec{B H} = - 2 \vec{C H}$ Biết thể tích khối chóp S.ABC bằng $\frac{a^{3} \sqrt{3}}{6}$ thì góc giữa SB và mặt phăng (ABC) bằng α. Giá trị tan $α$ bằng bao nhiêu?

tan $α$ = $\frac{2}{3}$

tan $α$ = $3$

tan $α$ = $\frac{3}{2}$

tan $α$ = 2

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết BC = a $\sqrt{3}$ . Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA = a. Góc giữa SD với mặt phẳng (SAB) là:

30^o

45^o

60^o

90^o

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = 2a, AD = a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB. Góc giữa SC với mặt phẳng đáy bằng 45°. Khoảng cách từ điểm A đến mặt phẳng (SCD) là:

$\frac{a \sqrt{3}}{3}$

$\frac{a \sqrt{6}}{4}$

$\frac{a \sqrt{6}}{3}$

$\frac{a \sqrt{3}}{6}$

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Gọi K là trung điểm DD’. Khoảng cách giữa hai đường thẳng CK và A'D là:

$\frac{4 a}{3}$

$\frac{a}{3}$

$\frac{2 a}{3}$

$\frac{3 a}{3}$

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n $\geq$ 2). Biết rằng có 1725 tam giác có các đỉnh là ba trong số các điểm thuộc d1 và d2 nói trên. Khi đó n bằng bao nhiêu?

n = 12

n = 13

n = 14

n = 15

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp tứ giác S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AD = 2a, SA $⊥$ (ABCD). Tính khoảng cách giữa BD và SC.

$\frac{3 a \sqrt{2}}{4}$

$\frac{a \sqrt{2}}{4}$

$\frac{5 a \sqrt{2}}{12}$

$\frac{5 a \sqrt{2}}{4}$

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x (0 < x < h). (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Giá trị x theo h để thể tích khối nón đỉnh O đáy là (C) lớn nhất là:

x = $\frac{h}{2}$

x = $\frac{h \sqrt{2}}{2}$

x = $\frac{h \sqrt{3}}{2}$

x = $\frac{h}{3}$

Xem đáp án

30. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình cầu đường kính 2a $\sqrt{3}$ . Mặt phẳng (P) cắt hình cầu theo thiết diện là hình tròn có bán kính bằng a $\sqrt{2}$ . Tính khoảng cách từ tâm hình cầu đến mặt phẳng (P).

$\frac{a}{2}$

$a \sqrt{10}$

$\frac{a \sqrt{10}}{2}$

Xem đáp án