25 câu hỏi
Nếu hai đường tròn tiếp xúc nhau thì số điểm chung của hai đường tròn là:
\[1\].
\[2\].
\[3\].
\[4\].
Nếu hai đường tròn không cắt nhau thì số điểm chung của hai đường tròn là:
\[1\].
\[2\].
\[3\].
\[0\].
Cho hai đường tròn \[(O;R)\] và \[(O';r)\] với \[R > r\] cắt nhau tại hai điểm phân biệt và \[OO' = d\]. Chọn khẳng định đúng?
\[d = R - r\].
\[d > R + r\].
\[R - r < d < R + r\].
>
\[d < R - r\].
>
Cho hai đường tròn \[(O;8cm)\] và \[(O';6cm)\] cắt nhau tại \[A,B\] sao cho \[OA\] là tiếp tuyến của \[(O')\]. Độ dài dây \[AB\] là:
\[AB = 8,6cm\].
\[AB = 6,9cm\].
\[AB = 4,8cm\].
\[AB = 9,6cm\].
Cho hai đường tròn \[(O;6cm)\] và \[(O';2cm)\] cắt nhau tại \[A,B\] sao cho \[OA\] là tiếp tuyến của \[(O')\]. Độ dài dây \[AB\] là:
\[AB = 3\sqrt {10} cm\].
\[AB = \frac{{6\sqrt {10} }}{5}cm\].
\[AB = \frac{{3\sqrt {10} }}{5}cm\].
\[AB = \frac{{\sqrt {10} }}{5}cm\].
Cho đường tròn \[(O)\] bán kính \[OA\] và đường tròn \[(O')\] đường kính \[OA\]. Vị trí tương đối của hai đường tròn là:
Nằm ngoài nhau.
Cắt nhau.
Tiếp xúc ngoài.
Tiếp xúc trong.
Cho đường tròn \[(O)\] bán kính \[OA\] và đường tròn \[(O')\] đường kính \[OA\]. Dây \[AD\] của đường tròn cắt đường tròn nhỏ tại \[C\]. Khi đó:
\[AC > CD\].
\[AC = CD\].
\[AC < CD\].
>
\[CD = OD\].
Cho đoạn \[OO'\] và điểm \[A\] nằm trên đoạn \[OO'\] sao cho \[OA = 2O'A\]. Đường tròn \[(O)\] bán kính \[OA\] và đường tròn \[(O')\] bán kính \[O'A\]. Vị trí tương đối của hai đường tròn là:
Nằm ngoài nhau.
Cắt nhau.
Tiếp xúc ngoài.
Tiếp xúc trong.
Cho hai đường tròn \[(O;20cm)\] và \[(O';15cm)\] cắt nhau tại \[A\] và \[B\]. Tính đoạn nối tâm \[OO'\], biết rằng \[AB = 24cm\] và \[O\] và \[O'\] nằm cùng phía đối với \[AB\].
\[OO' = 7cm\].
\[OO' = 8cm\].
\[OO' = 9cm\].
\[OO' = 25cm\].
Cho hai đường tròn \[(O;10cm)\] và \[(O';5cm)\] cắt nhau tại \[A\] và \[B\]. Tính đoạn nối tâm \[OO'\], biết rằng \[AB = 8cm\] và \[O\] và \[O'\] nằm cùng phía đối với \[AB\]. (làm tròn đến chữ số thập phân thứ nhất).
\[OO' \approx 6,5cm\].
\[OO' \approx 6,1cm\].
\[OO' \approx 6cm\].
\[OO' \approx 6,2cm\].
Cho hai đường tròn \[(O);(O')\] tiếp xúc ngoài tại \[A\]. Kẻ tiếp tuyến chung ngoài \[MN\] với \[M \in (O);N \in (O')\]. Gọi \[P\] là điểm đối xứng với \[M\] qua \[OO';Q\] là điểm đối xứng với \[N\] qua \[OO'\].Khi đó, tứ giác \[MNQP\] là hình gì?
Hình thang cân.
Hình thang.
Hình thang vuông.
Hình bình hành.
Cho hai đường tròn \[(O);(O')\] cắt nhau tại \[A,B\] trong đó \[O' \in (O)\]. Kẻ đường kính \[O'C\] của đường tròn \[(O)\]. Chọn khẳng định sai?
\[AC = CB\].
\[\widehat {CBO'} = 90^\circ \].
\[CA,CB\] là hai tiếp tuyến của \[(O')\].
\[CA,CB\] là hai cát tuyến của \[(O')\].
Cho hình vuông \(ABCD\) cạnh bằng \(2cm.\) Gọi \(I;\,J\) lần lượt là trung điểm của \(AC;\,CD.\) Vị trí tương đối của đường tròn\((A;\,AI)\) và \((C;\,CJ)\) là
trong nhau.
tiếp xúc ngoài.
ngoài nhau.
cắt nhau.
Cho hai đường tròn \(({O_1})\) và \(({O_2})\)tiếp xúc ngoài tại \(A\)và một đường thẳng \(d\)tiếp xúc với \(({O_1})\); \(({O_2})\)lần lượt tại \(B;\,C.\) Lấy \(M\)là trung điểm của \(BC.\)
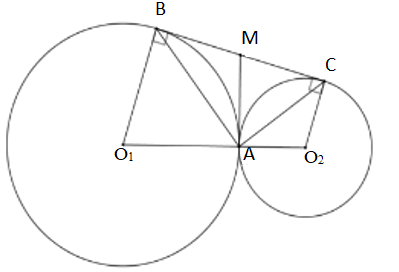
Chọn khẳng định sai trong các khẳng định sau:
\(AM = \frac{{B{O_1} + C{O_2}}}{2}\)
\(AM \bot A{O_1};AM \bot A{O_2}\)
\(AM = \frac{1}{2}BC\)
\(AM = MC\)
Cho \(({O_1};\,3cm)\) tiếp xúc ngoài với \(({O_2};\,1cm)\). Vẽ bán kính \({O_1}B\) và \({O_2}C\) song song với nhau cùng thuộc một nửa mặt phẳng bờ \({O_1}{O_2}.\) Gọi \(D\)là giao điểm của \(BC\) và \({O_1}{O_2}.\) Số đo \(\widehat {BAC}\)là:
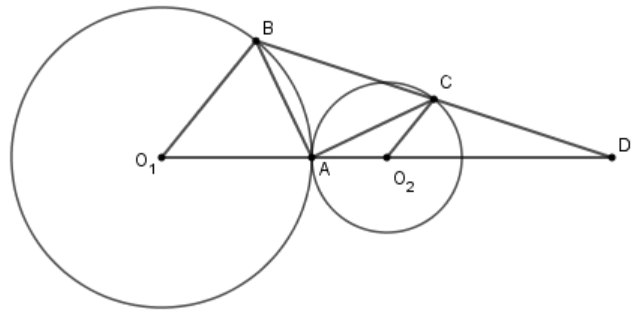
\({90^0}\)
\({60^0}\)
\({80^0}\)
\({100^0}\)
Cho hai đường tròn \(\left( {O\,;7cm} \right)\) và \(\left( {O'\,;3cm} \right)\). Biết rằng \[OO' = 4cm\]. Vị trí tương đối của hai đường tròn là
cắt nhau.
không giao nhau.
tiếp xúc trong.
tiếp xúc ngoài.
Biết rằng hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';1cm} \right)\) tiếp xúc ngoài. Vẽ tiếp tuyến chung ngoài \(BC\) của hai đường tròn, \(B \in \left( O \right)\), \(C \in \left( {O'} \right)\). Độ dài đoạn thẳng \(BC\) bằng
\(4cm\).
\(3cm\).
\(5cm\).
\(2cm\).
Cho hai đường tròn \[\left( {O;\,8cm} \right)\] và \[\left( {O';\,3cm} \right)\]. Biết rằng \[{\rm{OO' = 4}}{\mathop{\rm cm}\nolimits} \], vị trí tương đối của hai đường tròn là.
Cắt nhau.
Tiếp xúc nhau.
\[\left( O \right)\] đựng \[\left( {O'} \right)\].
Ở ngoài nhau.
Cho hai đường tròn \[\left( {O;\,4cm} \right)\] và \[\left( {O';\,3cm} \right)\]. Điều kiện để hai đường tròn cắt nhau là.
\[{\rm{OO'}}\,\,{\rm{ < }}\,\,{\rm{7}}{\mathop{\rm cm}\nolimits} \].
\[{\rm{1cm}}\,\, \le \,\,{\rm{OO'}}\,\, \le \,\,{\rm{7}}{\mathop{\rm cm}\nolimits} \].
\[{\rm{OO'}}\,\, \ge \,1{\mathop{\rm cm}\nolimits} \].
\[{\rm{1cm}}\,\, < \,\,{\rm{OO'}}\,\,{\rm{ < }}\,\,{\rm{7}}{\mathop{\rm cm}\nolimits} \].
Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\]\[\left( {R \ge r} \right)\]. Khẳng định nào sau đây là đúng.
Khi \[{\rm{OO}}'\, < \,R + r\] thì hai đường tròn cắt nhau.
Hai đường tròn cắt nhau khi \[R,r,{\rm{OO}}'\] là độ dài ba cạnh của một tam giác.
Hai đường tròn không giao nhau \[ \Leftrightarrow {\rm{OO}}'\, > \,R + r\].
Hai đường tròn tiếp xúc nhau \[ \Leftrightarrow {\rm{OO}}'\, = \,R + r\].
Tìm khẳng định sai trong các khẳng định sau:
Hai đường tròn tiếp xúc ngoài có \(3\) tiếp tuyến chung.
Hai đường tròn ở ngoài nhau có \(2\) tiếp tuyến chung.
Hai đường tròn tiếp xúc trong có \(1\) tiếp tuyến chung.
Hai đường tròn có một đường tròn đựng đường tròn kia thì chúng không có tiếp tuyến chung.
Hai đường tròn \(\left( {O;8cm} \right)\) và \(\left( {O';2cm} \right)\) cắt nhau. Số giá trị nguyên mà độ dài \(OO'\) có thể nhận là
\(3\).
\(2\).
\(4\).
\(5\).
Cho tam giác \(ABC\) vuông tại \(A\)(\(AB < AC\)). Đường trung trực của \(BC\) cắt \(BC,AC,AB\) theo thứ tự ở \(E;F;G\). Vị trí tương đối của \(EA\) và đường tròn đường kính \(FG\) là:
</>
Cắt nhau.
Không giao nhau.
Tiếp xúc nhau.
Không xác định được.
Hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại \(A\) và \(B\). Trong các khẳng định sau:
a) \(AB\) vuông góc với \(OO'\);
b) \(AB\) là đường trung trực của \(OO'\);
c) \(A\) và \(B\) luôn nằm trên nửa mặt phẳng đối nhau bở \(OO'\);
d) \(\left( O \right)\) và \(\left( {O'} \right)\) luôn nằm trên hai nửa mặt phẳng đối nhau bờ \(AB\).
Có bao nhiêu khẳng định đúng?
\(1\).
\(2\).
\(3\).
\(4\).
Cho hai đường tròn \(\left( {O;R} \right)\) và tiếp xúc ngoài tại \(A\). Tiếp tuyến chung ngoài \(BC\) cắt đường nối tâm ở \(M\), trong đó \(B \in \left( O \right)\), \(C \in \left( {O'} \right)\) và \(BC = CM = 4cm\). Tổng \(R + r\) bằng
\(4cm\).
\(3\sqrt 2 cm\).
\(6cm\).
\(5\sqrt 2 cm\).
Gợi ý cho bạn
Xem tất cả54 bài tập Một số yếu tố xác suất có lời giải
39 bài tập Tứ giác nội tiếp có lời giải
50 bài tập Hình khối trong thực tiễn có lời giải
35 bài tập Đa giác đều. Phép quay có lời giải
90 bài tập Một số yếu tố thống kê có lời giải