200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao (P2)
25 câu hỏi
Rút gọn
logx2012!
logx1002!
logx2011!
logx2011.
Kết quả rút gọn của biểu thức là:
logab
Cho a; b > 0, Nếu viết thì xy bằng bao nhiêu ?
-1/3
1/3
3
- 3
Thu gọn biểu thức ta được:
Cho các số thực a; b; c thỏa mãn: . Giá trị của biểu thức là:
519
729
469
129
Tính giá trị của biểu thức
P = 1
P = 1/2
P= 0
P = 2
Cho x; y là các số thực lớn hơn thoả mãn x2 + 9y2 = 6xy . Tính
M = 1/4.
M = 1.
M = 1/2.
M = 1/3.
Cho f(1) = 1; f(m + n) = f(m) + f( n) + m.n với các số nguyên dương m; n .Khi đó giá trị của biểu thức là
3
4
6
9
Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức
19.
13.
14.
15.
Cho log9x = log12y = log16 (x + y). Giá trị của tỉ số x/y là:
Cho x; y > 0 thỏa mãn log2x + log2y = log4( x + y) Tìm x; y để biểu thức P = x2 + y2 đạt giá trị nhỏ nhất.
x = y= 1
Cho với b> a > 1 và P = log2ab + 54logba. Khi đó giá trị của m để P đạt giá trị nhỏ nhất là?
2
3
4
5
Cho a; b; c lần lượt là độ dài của hai cạnh góc vuông và cạnh huyền của một tam giác vuông, trong đó c - b và c + b khác 1. Khi đó logc+ba + logc-ba bằng:
-2logc+ba.logc-ba.
3logc+ba.logc-ba.
2logc+ba.logc-ba.
Tất cả sai
Cho hai số thực a; b với 1< a< b. Khẳng định nào sau đây là khẳng định đúng?
logab < 1 < logba
b < loga1 < log ba
logab < logba < 1
logba < 1 < logab
Cho a; b > 0 thỏa mãn a2 + b 2 = 7ab. Chọn mệnh đề đúng trong các mệnh đề sau?
3log(a+b) = (loga+logb)
2( loga + logb) = log( 7ab) .
log(a+b) =(loga+logb)
Cho x; y; z là các số thực dương tùy ý khác 1 và xyz khác 1. Đặt a = logxy; b = logzy. Mệnh đề nào sau đây đúng?
Cho các số dương a; b thõa mãn 4a2 + 9b2 = 13ab . Chọn câu trả lời đúng.
log=log+2log
log(2a+3b)=3log a+2logb
log=(loga+logb)
log=(loga+logb)
Cho x; y > 0 và x2 + 4y2 = 12xy . Khẳng định nào sau đây là khẳng định đúng?
log2=log2x-log2y
log2(x+2y)=2+(log2x+log2y)
log2(x + 2y) = log2x+log2y+1
4log2( x + 2y) = log2x + log2y.
Cho a; b; c> 0 đôi một khác nhau và khác 1, khẳng định nào sau đây là khẳng định đúng?
Cho a; b là các số thực dương thoả mãn a2 + b2 = 14ab . Khẳng định nào sau đây là sai ?
2log2(a + b) = 4 + log2a + log2b.
2log4(a + b) = 4 + log4a + log4b.
Với giá trị nào của m thì biểu thức xác định với mọi ?
m > -3
m < 3
Biểu thức ln( x2 - 2mx + 4) có nghĩa với mọi x khi
m = 2
-2 < m < 2
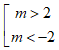
m < 2
Tìm x để ba số ln2; ln( 2x - 1); ln( 2x + 3) theo thứ tự lập thành cấp số cộng.
1
2
log25
log23
Biểu thức T = log2( ax2 - 4x + 1) có nghĩa với mọi x khi
0 < a < 4
a > 0
a > 4
Với giá trị nào của m thì biểu thức T = 34 + ln( 4m - x) xác định với mọi ?
m > -4
m -1/4
m < -4
m > -1/4








