30 câu hỏi
Cho ba điểm \[A\left( {1;0; - 2} \right),{\rm{ }}B\left( {2;1; - 1} \right),{\rm{ }}C\left( {1; - 2;2} \right)\] và điểm \(E\) là đỉnh thứ tư của hình bình hành \(ABCE\) thì tọa độ của \(E\) là
\(\left( {2; - 1 - 3} \right)\).
\(\left( {0; - 1;3} \right)\).
\(\left( {0; - 3;1} \right)\).
\(\left( {2; - 3;1} \right)\).
Cho 3 điểm \(M\left( {2;0;0} \right)\), \(N\left( {0; - 3;0} \right)\), \(P\left( {0;0;4} \right)\). Nếu \[MNPQ\] là hình bình hành thì tọa độ của điểm \(Q\) là
\(\left( {3;4;2} \right)\).
\(\left( {2;3;4} \right)\).
\(\left( { - 2; - 3; - 4} \right)\).
\(\left( {2;3; - 4} \right)\).
\(ABCD.A'B'C'D'\) có \(A\left( {0;0;1} \right)\), \(B'\left( {1;0;0} \right)\), \(C'\left( {1;1;0} \right)\)(tham khảo hình vẽ bên dưới). Tìm tọa độ của điểm \(D\).
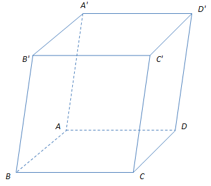
\(D\left( {0;1;1} \right)\).
\(D\left( {0; - 1;1} \right)\).
\(D\left( {0;1;0} \right)\).
\(D\left( {1;1;1} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\)cho hình hộp \[ABCD.A'B'C'D'\]. Biết \[A\left( {2;\,4;\,0} \right)\], \[B\left( {4;\,0;\,0} \right)\], \[C\left( { - 1;\,4;\, - 7} \right)\]và \[D'\left( {6;\,8;\,10} \right)\]. Tọa độ điểm \[B'\] là
\[B'\left( {8;\,4;\,10} \right)\].
\[B'\left( {6;\,12;\,0} \right)\].
\[B'\left( {10;\,8;\,6} \right)\].
\[B'\left( {13;\,0;\,17} \right)\].
Trong không gian với hệ toạ độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \[A\left( {0;\,\,0;\,\,0} \right)\], \[B\left( {3;\,\,0;\,\,0} \right)\], \[D\left( {0;\,\,3;\,\,0} \right)\], \[D'\left( {0;\,\,3;\,\, - 3} \right)\]. Toạ độ trọng tâm tam giác \(A'B'C\) là
\(\left( {1;\,\,1;\,\, - 2} \right)\).
\(\left( {2;\,\,1;\,\, - 2} \right)\).
\(\left( {1;\,\,2;\,\, - 1} \right)\).
\(\left( {2\,;\,\,1;\,\, - 1} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho tam giác \(ABC\) với \(A\left( {1;1;1} \right)\), \(B\left( {2;3;0} \right)\). Biết rằng tam giác \(ABC\) có trực tâm \(H\left( {0;3;2} \right)\) tìm tọa độ của điểm \(C\).
\(C\left( {3;2;3} \right)\).
\(C\left( {4;2;4} \right)\).
\(C\left( {1;2;1} \right)\).
\(C\left( {2;2;2} \right)\).
Trong không gian \[Oxyz\], cho hình hộp \(ABCD.A'B'C'D'\)biết \(A\left( {1\,;\,0\,;\,1} \right)\), \(B\left( {2\,;\,1\,;\,2} \right)\), \(D\left( {1\,;\, - 1\,;\,1} \right)\), \(C'\left( {4\,;\,5\,;\, - 5} \right)\). Tọa độ của đỉnh \(A'\) là
\(A' = \left( {4\,;\,5\,;\, - 6} \right)\).
\(A' = \left( {3\,;\,4\,;\, - 1} \right)\).
\(A' = \left( {3\,;\,5\,;\, - 6} \right)\).
\(A' = \left( {3\,;\,5\,;\,6} \right)\).
Trong không gian \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {0;0;1} \right)\), \(B'\left( {1;0;0} \right)\), \(C'\left( {1;1;0} \right)\)(tham khảo hình vẽ bên dưới). Tìm tọa độ của điểm \(D\).
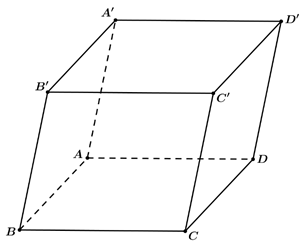
\(D\left( {0;1;1} \right)\).
\(D\left( {0; - 1;1} \right)\).
\(D\left( {0;1;0} \right)\).
\(D\left( {1;1;1} \right)\).
Trong không gian với hệ toạ độ Oxyz, cho 3 điểm A(2; 3; 1), B(3; 2; 1), C(1; 3; 2). Gọi H(a, b , c) là trực tâm tam giác. Giá trị của 2a + b + c là
10
6
8
9
Trong không gian \[Oxyz\] cho ba điểm \[A\left( {1;4; - 5} \right),B\left( {2;3; - 6} \right),C\left( {4;4; - 5} \right)\]. Tìm tọa độ trực tâm \[H\] của tam giác \[ABC\].
\[H\left( {\frac{5}{2};4; - 5} \right)\].
\[H\left( {1;4; - 5} \right)\].
\[H\left( {2;3; - 6} \right)\].
\[H\left( {\frac{7}{3};\frac{{11}}{3}; - \frac{{16}}{3}} \right)\].
Trong không gian với hệ tọa độ \[Oxyz\], cho ba điểm \[A\left( {1;\,2;\, - 1} \right)\], \[B\left( {2;\, - 1;\,3} \right)\], \[C\left( { - 4;\,7;\,5} \right)\]. Tọa độ chân đường phân giác trong góc \[B\] của tam giác \[ABC\] là
\[\left( { - \frac{2}{3};\,\frac{{11}}{3};\,1} \right)\].
\[\left( {\frac{{11}}{3};\, - 2;\,1} \right)\].
\[\left( {\frac{2}{3};\,\frac{{11}}{3};\,\frac{1}{3}} \right)\].
\[\left( { - 2;\,11;\,1} \right)\].
Trong không gian với hệ toạ độ \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {2;2;1} \right)\), \(B\left( {4;4;2} \right)\), \(C\left( { - 2;4; - 3} \right)\). Đường phân giác trong \(AD\) của tam giác \(ABC\)có một vectơ chỉ phương là:
\(\left( { - 2;4; - 3} \right)\).
\(\left( {6;0;5} \right)\).
\(\left( {0;1; - \frac{1}{3}} \right)\).
\(\left( { - \frac{4}{3}; - \frac{1}{3}; - 1} \right)\).
Trong không gian tọa độ \(Oxyz\)cho hai điểm \(A\left( {2;2;1} \right)\), \(B\left( { - \frac{8}{3};\frac{4}{3};\frac{8}{3}} \right)\). Biết \(I\left( {a;b;c} \right)\)là tâm đường tròn nội tiếp của tam giác \(OAB\). Tính \(S = a + b + c.\)
\(S = 1\).
\(S = 0\).
\(S = - 1\).
\(S = 2\).
Trong không gian \(Oxyz\)cho ba điểm \(A\left( {1;2;3} \right)\), \(B\left( {3;4;4} \right)\), \(C\left( {2;6;6} \right)\) và \(I\left( {a;b;c} \right)\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Tính \(a + b + c\).
\(\frac{{31}}{3}\).
\(\frac{{46}}{5}\).
\(10\).
\(\frac{{63}}{5}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\) có \(A(3;1;0)\), \(B\) nằm trên mặt phẳng \((Oxy)\) và có hoành độ dương, \(C\) nằm trên trục \(Oz\) và \(H(2;1;1)\) là trực tâm của tam giác \(ABC\). Toạ độ các điểm \(B\), \(C\) thỏa mãn yêu cầu bài toán là
\[B(3;1;0),{\rm{ }}C(0;0; - 3)\].
\[B(1;3;0),{\rm{ }}C(0;0; - 3)\].
\[B(3; - 3;0),{\rm{ }}C(0;0;1)\].
\[B(1; - 3;0),{\rm{ }}C(0;0;1)\].
Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {1;2; - 1} \right)\), \(B\left( {2; - 1;3} \right),C\left( { - 4;7;5} \right)\). Gọi \(D\left( {a;b;c} \right)\) là chân đường phân giác trong của góc \(B\) của tam giác \(ABC\). Giá trị \(a + b + 2c\) bằng
\(4\).
\(5\).
\(14\).
\(15\).
Trong không gian với tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;\,1;\,2} \right)\), \(B\left( { - 1;\,3;\, - 9} \right)\). Tìm tọa độ điểm \(M\)thuộc \(Oy\) sao cho \(\Delta ABM\)vuông tại \(M\).
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1; - 2;2} \right)\), \(B\left( { - 5;6;4} \right)\) và \(C\left( {0;1; - 2} \right)\). Độ dài đường phân giác trong của góc \(A\) của \(\Delta ABC\) là:
\[\frac{{3\sqrt {74} }}{2}\].
\[\frac{3}{{2\sqrt {74} }}\].
\[\frac{2}{{3\sqrt {74} }}\].
\[\frac{{2\sqrt {74} }}{3}\].
Trong không gian \[Oxyz\] cho các điểm \[A\left( {5\,;\,1\,;\,5} \right)\], \[B\left( {4\,;\,3\,;\,2} \right)\], \[C\left( { - 3\,;\, - 2\,;\,1} \right)\]. Điểm \[I\left( {a\,;\,b\,;\,c} \right)\] là tâm đường tròn ngoại tiếp tam giác \[ABC\]. Tính \[a + 2b + c\]?
\[1\].
\[3\].
\[6\].
\[ - 9\].
Trong không gian \(Oxyz\), cho \(\vec a = \left( {1; - 2;3} \right)\) và \(\vec b = \left( {3;0;4} \right)\). Tính \(\vec a.\vec b\).
15.
36.
9.
5.
Trong không gian với hệ tọa độ \(Oxyz\), cho \(\vec u = (x;2;1),\) \(\vec v = (1; - 1;2x)\). Tích vô hướng của \(\vec u\) và \(\vec v\).
\(x + 2\).
\(3x + 2\).
\( - 2 - x\).
\(3x - 2\).
Trong không gian \(Oxyz\), cho các vectơ \(\vec a = \left( {1;3;3} \right)\), \(\vec b = \left( { - 2;2;1} \right)\) và \(\vec c = \left( { - 1;2;3} \right)\). Tích vô hướng \(\vec c.\left( {\vec a - \vec b} \right)\) bằng
\(7\).
\(5\)
\(9\).
\(3\).
Trong không gian \(Oxyz\) , cho \(A\left( {1; - 2;3} \right),\,B\left( {2; - 4;1} \right),\,C\left( {2;0;2} \right)\) , khi đó tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng
\(7.\)
\( - 5.\)
\(4.\)
\( - 1.\)
Trong không gian \(Oxyz\), cho hai điểm \(A\left( { - 2\,;\,1\,;\,1} \right)\), \(B\left( {3\,;\,2\,;\, - 1} \right)\). Độ dài đoạn thẳng \(AB\) bằng
\(\sqrt {30} \).
\(\sqrt {10} \).
\(\sqrt {22} \).
\(2\).
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;{\rm{ }} - 1;{\rm{ }}2} \right)\) và \(B\left( {2;{\rm{ }}1;{\rm{ }}1} \right)\). Độ dài đoạn \(AB\) bằng
\(2\).
\(\sqrt 6 \).
\(\sqrt 2 \).
\(6\).
Trong không gian \(Oxyz\), cho hai véc tơ \(\overrightarrow u = \left( {2;3; - 1} \right)\) và \(\overrightarrow v = \left( {5; - 4;x} \right).\) Tìm \(x\) để \(\overrightarrow u .\overrightarrow v = 0\)
\(x = 2\).
\(x = 22\).
\(x = \frac{{ - 3}}{{10}}\) .
\(x = - 2\).
Cho hai vec tơ \(\overrightarrow a = \left( {1; - 2;3} \right),\,\overrightarrow b = \left( { - 2;1;2} \right).\) Khi đó tích vô hướng \(\left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow b \) bằng
\(12\).
\(2\).
\(11\).
\(10\).
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {2;3;4} \right)\) và \(B\left( {3;0;1} \right)\). Độ dài vectơ \(\overrightarrow {AB} \) là
\(\sqrt {19} \).
19.
\(\sqrt {13} \).
13.
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \[A\left( { - 1;3;1} \right),B(2;0; - 5)\]. Tính \[\overrightarrow {AB} .\overrightarrow {OB} \].
\( - 12\).
\( - 36\).
\[36\].
\[12\].
Trong không gian với hệ tọa độ \[{\rm{Ox}}yz\], cho hai vectơ \(\overrightarrow a = \left( {2; - 3;1} \right)\) và \(\overrightarrow b = \left( { - 1;4; - 2} \right)\). Giá trị của biểu thức \(\overrightarrow a .\overrightarrow b \) bằng
\( - 16\).
\( - 4\).
\(4\).
\(16\).
