30 câu hỏi
Trong không gian \[Oxyz\], cho hai điểm \[A\left( {1;\,3;\,5} \right)\] và \[B\left( {1;\, - 1;\,1} \right)\]. Trung điểm của đoạn thẳng \[AB\] có tọa độ là
\[\left( {2;2;\,6} \right)\].
\[\left( {0;\, - 4;\, - 4} \right)\].
\[\left( {0;\, - 2;\, - 2} \right)\].
\[\left( {1;\,1;\,3} \right)\].
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;\,1;\, - 1} \right)\) và \(B\left( {2;\,3;\,2} \right)\). Véctơ \(\overrightarrow {AB} \) có tọa độ là
\(\left( {1;\,2;\,3} \right)\).
\(\left( { - 1;\, - 2;\,3} \right)\).
\(\left( {3;\,5;\,1} \right)\).
\(\left( {3;\,4;\,1} \right)\).
Trong không gian \(Oxyz\), điểm đối xứng với điểm \(M\left( {2020\,; - 2021\,;\,2020} \right)\) qua trục \(Ox\) có tọa độ là
\(N\left( {2020\,;2021\,;2020} \right)\).
\(N\left( {2020\,;2021\,; - 2020} \right)\).
\(N\left( { - 2020\,;2021\,; - 2020} \right)\).
\(N\left( {2020\,;0\,;0} \right)\).
Trong không gian với hệ trục tọa độ \[Oxyz\], cho \[2\] điểm \[A\left( {2;1;1} \right)\], \[B\left( { - 1;2;1} \right)\]. Tìm tọa độ điểm \[A'\] đối xứng với điểm \[A\] qua điểm \[B\].
\[A'\left( {3;4; - 3} \right)\].
\[A'\left( { - 4;3;1} \right)\].
\[A'\left( {4; - 3;3} \right)\].
\[A'\left( {4;3;3} \right)\].
Trong không gian \[Oxyz\], cho hai điểm \[A\left( {1;1; - 2} \right)\], \[B\left( {3; - 4;1} \right)\]. Tọa độ của vectơ \[\overrightarrow {AB} \] là
\[\left( { - 2;5; - 3} \right)\].
\[\left( {2;5;3} \right)\].
\[\left( {2; - 5;3} \right)\].
\[\left( {2;5; - 3} \right)\].
Trong không gian với hệ toạ độ \(Oxyz\), cho hai điểm \(A\left( {2; - 1;3} \right)\)và \(B\left( {4; - 3; - 1} \right)\). Toạ độ trung điểm của đoạn thẳng \(AB\)là
\(\left( {2; - 2; - 4} \right).\)
\(\left( {3; - 2;1} \right).\)
\(\left( {1; - 1; - 2} \right).\)
\(\left( {6; - 4; - 2} \right).\)
Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {0;\,1;\,3} \right)\), \(\overrightarrow b = \left( { - 2;\,3;\,1} \right)\). Tìm tọa độ của vectơ \(\overrightarrow x \) biết \(\overrightarrow x = 3\overrightarrow a + 2\overrightarrow b \)
\(\overrightarrow x = \left( { - 2;\,4;\,4} \right)\).
\(\overrightarrow x = \left( {4;\, - 3;\,7} \right)\).
\(\overrightarrow x = \left( { - 4;\,9;\,11} \right)\).
\(\overrightarrow x = \left( { - 1;\,9;\,11} \right)\).
Trong không gian với hệ trục toạ độ \(Oxyz\), cho \(\vec a = \left( {2;\,3;\,1} \right)\), \(\vec b = \left( { - 1;\,5;\,2} \right)\), \(\vec c = \left( {4;\, - 1;\,3} \right)\) và \(\vec x = \left( { - 3;\,22;\,5} \right)\). Đẳng thức nào đúng trong các đẳng thức sau ?
\(\vec x = 2\vec a - 3\vec b - \vec c\).
\(\vec x = - 2\vec a + 3\vec b + \vec c\).
\(\vec x = 2\vec a + 3\vec b - \vec c\).
\(\vec x = 2\vec a - 3\vec b + \vec c\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( { - 4;5; - 3} \right)\), \(\overrightarrow b = \left( {2; - 2;1} \right)\). Tìm tọa độ của vectơ \(\overrightarrow x = \overrightarrow a + 2\overrightarrow b \).
\(\overrightarrow x = \left( {2;3; - 2} \right)\).
\(\vec x = \left( {0;1; - 1} \right)\).
\(\overrightarrow x = \left( {0; - 1;1} \right)\).
\(\overrightarrow x = \left( { - 8;9;1} \right)\).
Cho hai điểm \(M\left( {1; - 2;3} \right)\) và \(N\left( {3;0; - 1} \right)\). Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(MN\).
\(I\left( {4; - 2;2} \right)\).
\(I\left( {2; - 1;2} \right)\).
\(I\left( {4; - 2;1} \right)\).
\(I\left( {2; - 1;1} \right)\).
Trong không gian \(Oxyz\), cho ba vectơ \(\vec a = \left( {1;2;3} \right)\), \(\vec b = \left( { - 2;0;1} \right)\), \(\vec c = \left( { - 1;0;1} \right)\). Tìm tọa độ của vectơ \(\vec n = \vec a + \vec b + 2\vec c - 3\vec i\).
\(\vec n = \left( {6;2;6} \right)\).
\(\vec n = \left( {6;2; - 6} \right)\).
\(\vec n = \left( {0;2;6} \right)\).
\(\vec n = \left( { - 6;2;6} \right)\).
Trong không gian với hệ tọa độ \(Oxyz,\) cho hai điểm \(A\left( {2;{\rm{ }}3;{\rm{ }}4} \right)\), \(B\left( {6;{\rm{ }}2;{\rm{ }}2} \right)\). Tìm tọa độ véctơ \(\overrightarrow {AB} .\)
\(\overrightarrow {AB} = \left( {4;3;4} \right)\).
\(\overrightarrow {AB} = \left( {4; - 1; - 2} \right)\).
\(\overrightarrow {AB} = \left( { - 2;3;4} \right)\).
\(\overrightarrow {AB} = \left( {4; - 1;4} \right)\).
Trong không gian \[Oxyz\], cho ba điểm\(A\left( {3\,;\,5\,;\, - 1} \right)\), \(B\left( {7\,;\,x\,;\,1} \right)\)và \(C\left( {9\,;\,2\,;\,y} \right)\). Để \(A\), \(B\), \(C\) thẳng hàng thì giá trị \(x + y\) bằng
\(5\).
\(6\).
\(4\).
\(7\).
Trong không gian với hệ trục toạ độ \(Oxyz\), cho các vectơ \(\vec a = \left( {1;2;1} \right)\), \(\vec b = \left( { - 2;3;4} \right)\), \(\vec c = \left( {0;1;2} \right)\) và \(\vec d = \left( {4;2;0} \right)\). Biết rằng \(\vec d = x.\vec a + y.\vec b + z.\vec c\). Giá trị \(x + y + z\) là
\(2\)
\(3\)
\(4\)
\(5\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\), biết tọa độ \(A\left( { - 3;2;1} \right)\), \(C\left( {4;2;0} \right)\), \(B'\left( { - 2;1;1} \right)\), \(D'\left( {3;5;4} \right)\). Tìm tọa độ \(A'\).
\[A'\left( { - 3;3;1} \right)\].
\(A'\left( { - 3;3;3} \right)\).
\(A'\left( { - 3; - 3; - 3} \right)\).
\(A'\left( { - 3; - 3;3} \right)\).
Trong không gian với hệ trục toạ độ \(Oxyz\), cho \(\vec a = \left( {10 - m;m + 2;{m^2} - 10} \right)\) và \(\vec b = \left( {7; - 1;3} \right)\). Giá trị của \(m\) để \(\vec a\) cùng phương với \(\vec b\) là
\(m = 4\).
\(m = - 4\).
\(m = - 2\).
\(m = 2\).
Trong không gian với hệ trục \(Oxyz\) cho ba điểm \(A\left( {2\,;\,1\,;\,3} \right)\), \(B\left( {1\,;\, - 2\,;\,2} \right)\), \(C\left( {x\,;\,y\,;\,5} \right)\) thẳng hàng. Khi đó \(x + y\) bằng
\(x + y = 11\).
\(x + y = 12\).
\(x + y = 9\).
\(x + y = 3\).
Trong không gian với hệ tọa độ \[Oxyz\], cho ba điểm\[A\left( {2;5;3} \right),\]\[B\left( {3;7;4} \right)\]và \[C\left( {x;y;6} \right)\] thẳng hàng. Giá trị của biểu thức \[x + y\] là
\(16\).
\(14\).
\(18\).
\(20\).
Trong hệ trục tọa độ \[Oxyz\], cho hai điểm là \[A\left( {1;3; - 1} \right)\], \[B\left( {3; - 1;5} \right)\]. Tìm tọa độ của điểm \[M\]thỏa mãn hệ thức \[\overrightarrow {MA} = 3\overrightarrow {MB} \].
\[M\left( {\frac{5}{3}{\kern 1pt} ;\frac{{13}}{3};1} \right)\].
\[M\left( {\frac{7}{3};\frac{1}{3}{\kern 1pt} ;3} \right)\].
\[M\left( {\frac{7}{3};\frac{1}{3};3} \right)\].
\[M\left( {4; - 3;8} \right)\].
Trong không gian với hệ tọa độ \[Oxyz\], cho ba điểm \[A\left( {2;0;0} \right)\], \[B\left( {0;3;1} \right)\], \[C\left( { - 3;6;4} \right)\]. Gọi \[M\] là điểm nằm trên đoạn \[BC\] sao cho \[MC = 2MB\]. Tính độ dài đoạn \[AM\].
\(AM = 3\sqrt 3 \)
\(AM = 2\sqrt 7 \).
\(AM = \sqrt {29} \).
\(AM = \sqrt {30} \).
Trong không gian \[Oxyz\], cho hai điểm \[A(1\,;2\,;3)\], \[B( - 2\,; - 4\,;9)\]. Điểm \[M\]thuộc đoạn thẳng \[AB\]sao cho \[MA = 2MB.\]Độ dài đoạn thẳng \[OM\] là:
5.
\[3.\]
\[\sqrt {17} \].
\[\sqrt {54} .\]
Trong không gian với hệ tọa độ \[Oxyz\], cho tam giác \(ABC\) có \(\overrightarrow {AB} = \left( { - 3\,;\,0\,;\,4} \right)\), \[\overrightarrow {AC} = \left( {5\,;\, - 2\,;\,4} \right)\]. Độ dài đường trung tuyến \(AM\) là
\(4\sqrt 2 \).
\(3\sqrt 2 \).
\(5\sqrt 2 \).
\(2\sqrt 3 \)
Trong không gian với hệ tọa độ \(Oxyz\), cho các điểm \(A\left( {2;\,\,0;\,\, - 1} \right)\), \(B\left( {0;\,\,3;\,\, - 2} \right)\),\(C\left( { - 4;\,\, - 5;\,\,0} \right)\). Tìm tọa độ điểm \(M\) sao cho \(\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} = \overrightarrow 0 \).
\(M\left( {\frac{5}{3};\, - \frac{3}{2};\,\,\frac{5}{6}} \right)\).
\(M\left( { - \frac{5}{3};\, - \frac{3}{2};\,\, - \frac{5}{6}} \right)\).
\(M\left( { - \frac{5}{3};\,\, - \frac{3}{2};\,\,\frac{5}{6}} \right)\).
\(M\left( {\frac{5}{3};\, - \frac{3}{2};\,\, - \frac{5}{6}} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho ba điểm \[A\left( {1;\,2;\, - 1} \right)\], \[B\left( {2;\, - 1;\,3} \right)\], \[C\left( { - 4;\,7;\,5} \right)\]. Tọa độ chân đường phân giác trong góc \[B\] của tam giác \[ABC\] là
\[\left( { - \frac{2}{3};\,\frac{{11}}{3};\,1} \right)\].
\[\left( {\frac{{11}}{3};\, - 2;\,1} \right)\].
\[\left( {\frac{2}{3};\,\frac{{11}}{3};\,\frac{1}{3}} \right)\].
\[\left( { - 2;\,11;\,1} \right)\].
Trong không gian với hệ tọa độ Oxyz ,để hai vec tơ \(\overrightarrow a = \left( {m;2;3} \right)\) và \(\overrightarrow b = \left( {1;n;2} \right)\) cùng phương thì \(2m + 3n\) bằng
\(7\).
\(8\).
\(6\).
\(9\).
Trong không gian với hệ trục \[Oxyz\], cho hai điểm \(A\left( { - 2\,;\,4\,;\,1} \right)\) và \(B\left( {4\,;\,5\,;\,2} \right)\). Điểm \[C\] thỏa mãn \[\overrightarrow {OC} = \overrightarrow {BA} \] có tọa độ là
\(\left( { - 6\,;\,\, - 1\,;\, - 1} \right)\).
\(\left( { - 2\,;\,\, - 9\,;\, - 3} \right)\).
\(\left( {6\,;\,\,1\,;\,1} \right)\).
\(\left( {2\,;\,\,9\,;\,3} \right)\).
Trong không gian Oxyz, cho các điểm \(A\left( {1;2;0} \right),B\left( { - 1;0;1} \right),C\left( {0;2; - 1} \right)\). Tính độ dài của vectơ \(\overrightarrow {AB} - 2\overrightarrow {AC} \).
\(\sqrt {21} \).
\(21\).
\(\sqrt {13} \).
\(13\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho ba điểm \(A\left( {1; - 1;1} \right)\,,\,B\left( {3;2; - 2} \right)\,,\,C\left( { - 3;1;5} \right)\). Tìm tọa độ điểm \(M\left( {x;y;z} \right)\) thỏa mãn \(\overrightarrow {MA} - 2\overrightarrow {AB} = 4\overrightarrow {CM} \). Khi đó tổng \(S = \frac{9}{x} + \frac{3}{y} - \frac{{27}}{z}\) bằng
\(6\).
\( - 15\).
\(16\).
\( - 13\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) biết \(A\left( {2\,;\, - 1\,;\,2} \right)\), \(B'\left( {1\,;\,2\,;\,1} \right)\), \(C\left( { - 2\,;\,3\,;\,2} \right)\), \(D'\left( {3\,;\,0\,;\,1} \right)\). Tọa độ điểm \(B\) là
\(B\left( { - 1\,;\,2\,;\,2} \right)\).
\(B\left( {2\,;\, - 2\,;\,1} \right)\).
\(B\left( {1\,;\, - 2\,;\, - 2} \right)\).
\(B\left( {2\,;\, - 1\,;\,2} \right)\).
Trong không gian \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {0\,;\,0\,;\,1} \right)\), \(B'{\kern 1pt} \left( {1\,;\,0\,;\,0} \right)\), \(C'\left( {1\,;\,1\,;\,0} \right)\). Tìm tọa độ điểm \(D\).
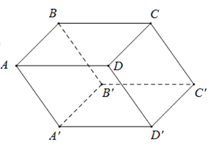
\(D\left( {0\,;\,1\,;\,1} \right)\)
\(D\left( {0\,;\, - 1\,;\,1} \right)\)
\(D\left( {0\,;\,1\,;\,0} \right)\)
\(D\left( {1\,;\,1\,;\,1} \right)\)
