15 câu Trắc nghiệm Toán lớp 10 Kết nối tri thức Hàm số bậc hai có đáp án
15 câu hỏi
Trục đối xứng của parabol y = x2 – 4x + 1
x = 2;
x = – 2;
x = 4;
x = – 4.
Tọa độ đỉnh I của hàm số y = – 3x2 + 4x – 1
\[{\rm{I}}\left( {--\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
\[{\rm{I}}\left( {\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
\[{\rm{I}}\left( {\frac{{\rm{4}}}{{\rm{3}}}{\rm{;}}--{\rm{1}}} \right)\];
\[{\rm{I}}\left( {\frac{2}{{\rm{3}}}{\rm{;}}\frac{4}{{\rm{3}}}} \right)\].
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
Hàm số đồng biến trên khoảng (0; + ∞);
Hàm số đồng biến trên khoảng (– ∞; 1);
Hàm số nghịch biến trên khoảng (– ∞; 0);
Hàm số nghịch biến trên khoảng (– ∞; 2).
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
a = 1; b = 2;
a = 1; b = – 2;
a = – 2; b = 4;
a = 2; b = 4.
Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
(– ∞; + ∞);
(– ∞; 1);
(1; + ∞);
(– ∞; 2).
Cho parabol có đồ thị như hình sau:
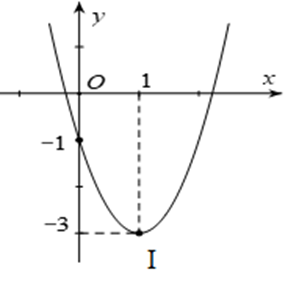
Tọa độ đỉnh I của parabol
I(– 1; – 3);
I(1; 0);
I(0; – 3);
I(1; – 3).
Cho hàm số y = f(x) có đồ thị như hình sau:
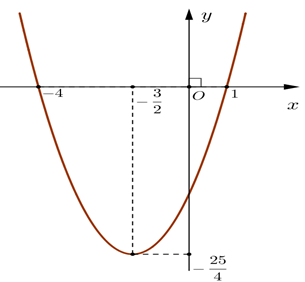
Hàm số đồng biến trên khoảng
\[\left( {--\infty {\rm{;}}--\frac{3}{2}} \right)\];
\[\left( {--\infty {\rm{;}}--\frac{{25}}{4}} \right)\];
\[\left( {--\frac{3}{2}; + \infty } \right)\];
\[\left( {--\frac{{{\rm{25}}}}{{\rm{4}}}; + \infty } \right)\].
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
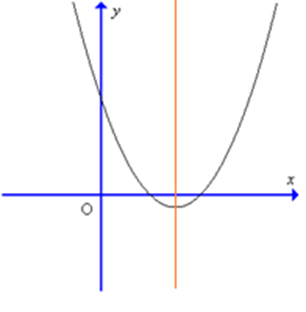
Kết luận nào sau đây đúng về hệ số a, b:
a > 0; b > 0;
a < 0; b > 0;
a > 0; b < 0;
a > 0; c <0.
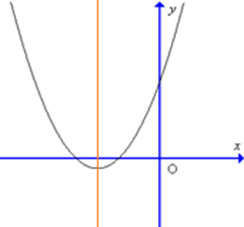
Hàm số y = x2 + 2x – 1 có bảng biến thiên là
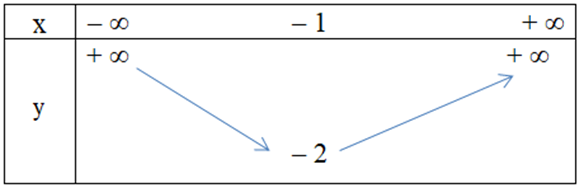
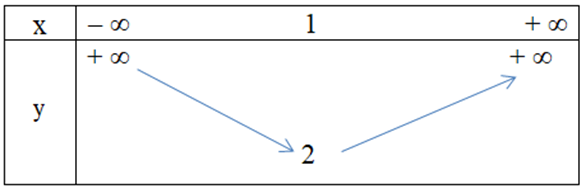
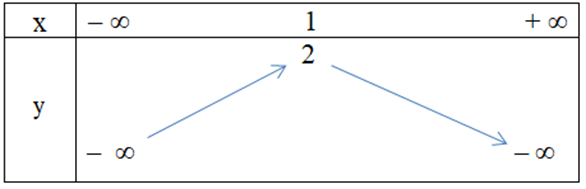
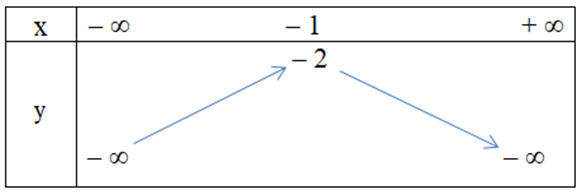
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
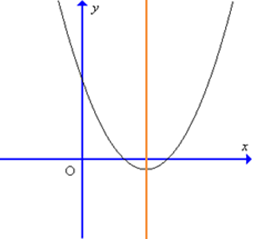
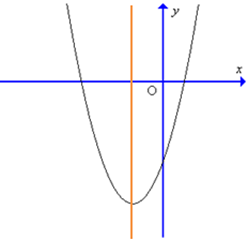
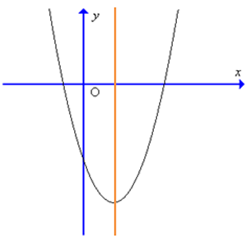
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
\[y = \frac{1}{2}{x^2} + 2x + 6\];
y = x2 + 2x + 6;
y = \(\frac{1}{2}\)x2 + 6x + 6;
y = x2 + x + 4.
Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
y = f(x) = x2 + 7x – 12;
y = f(x) = x2 – 7x – 12;
y = f(x) = x2 + 7x + 12;
y = f(x) = x2 – 7x + 12.
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?
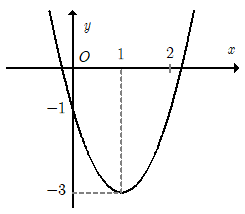
y = x2 – 4x – 1;
y = 2x2 – 4x – 1;
y = – 2x2 – 4x – 1;
y = 2x2 – 4x + 1.
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng \( - \frac{1}{4}\). Tính tích P = a.b.
P = – 3;
P = – 2;
P = 192;
P = 28.
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
S = – 1;
S = – 4;
S = 4;
S = 2.








