12 Bài tập Xét sự biến thiên của hàm số bậc hai (có lời giải)
12 câu hỏi
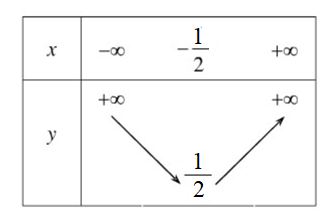
Xét sự biến thiên và lập bảng biến thiên của hàm số y = –x2 + 4x + 5.
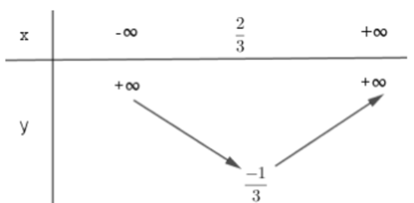
Xét sự biến thiên và lập bảng biến thiên của hàm số y = 2x2 + 2x + 1.
Hàm số y = x2 – 4x + 5 đồng biến trên khoảng:
(2; +∞);
(–∞; 2);
(–2; +∞);
(0; +∞).
Hàm số y = –3x2 + 6x + 1 đồng biến trên khoảng:
(–∞; 2);
(2; +∞);
(–∞; 1);
(1; +∞).
Hàm số y = –x2 + 2x – 2 nghịch biến trên khoảng:
(–∞; 2);
(2; +∞);
(–∞; 1);
(1; +∞).
Hàm số y = 4x2 – 24x – 6 nghịch biến trên khoảng:
(–∞; 3);
(4; +∞);
(–∞; 4);
(3; +∞).
Cho hàm số y = x2 – 4x – 6. Khẳng định nào sau đây là đúng ?
Hàm số đồng biến trên khoảng (–∞; 2);
Hàm số đồng biến trên khoảng (–∞; 4);
Hàm số nghịch biến trên khoảng (–∞; 2);
Hàm số nghịch biến trên khoảng (–∞; 4).
Cho hàm số y = –x2 + 8x – 3. Khẳng định nào sau đây là đúng ?
Hàm số đồng biến trên khoảng (–∞; 8);
Hàm số đồng biến trên khoảng (–∞; 4);
Hàm số nghịch biến trên khoảng (–∞; 4);
Hàm số nghịch biến trên khoảng (–∞; 8).
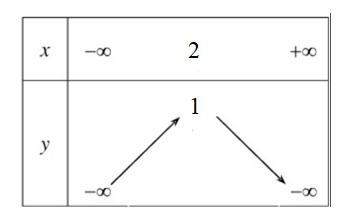
Cho hàm số y = –x2 + 4x – 3. Khẳng định nào sau đây là đúng ?
Hàm số đồng biến trên khoảng (–∞; 2) và nghịch biến trên khoảng (2; +∞);
Hàm số nghịch biến trên khoảng (–∞; 2) và đồng biến trên khoảng (2; +∞);
Hàm số đồng biến trên khoảng (–∞; 4) và nghịch biến trên khoảng (4; +∞);
Hàm số nghịch biến trên khoảng (–∞; 4) và đồng biến trên khoảng (4; +∞).
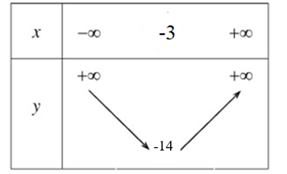
Cho hàm số y = x2 + 6x – 5. Khẳng định nào sau đây là đúng ?
Hàm số đồng biến trên khoảng (–∞; 3) và nghịch biến trên khoảng (3; +∞);
Hàm số nghịch biến trên khoảng (–∞; –3) và đồng biến trên khoảng (–3; +∞);
Hàm số đồng biến trên khoảng (–∞; –3) và nghịch biến trên khoảng (–3; +∞);
Hàm số nghịch biến trên khoảng (–∞; 3) và đồng biến trên khoảng (3; +∞).
Đâu là bảng biến thiên của hàm số y = –x2 + 4x – 3 ?
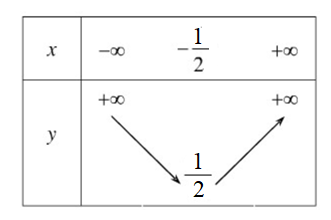
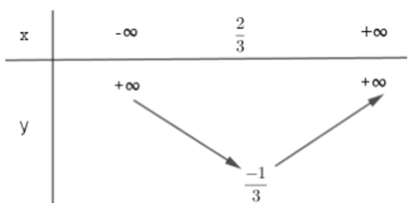
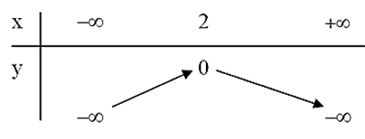
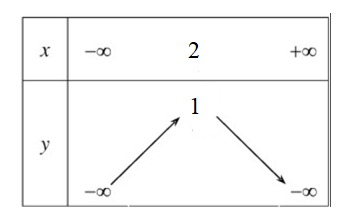
Đâu là bảng biến thiên của hàm số y = x2 + 6x – 5 ?