(Trả lời ngắn) 43 bài tập Phương trình mặt phẳng (có lời giải)- Đề 1
43 câu hỏi
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;1;-1), B(1;1;2),C(1;-1;0). Tính \[\left[ {\overrightarrow {BC} ,\overrightarrow {BD} } \right]\].
Trả lời: ………………………………
Trong không gian với hệ trục tọa độ Oxyz, cho A(2;0;2), B(1;-1;2) và C(-1;1;0). Tìm tọa độ vectơ \(\vec n\) có phương vuông góc với hai vectơ \[\overrightarrow {AB} \] và \[\overrightarrow {AC} \].
Trả lời: ………………………………
Trong hệ trục tọa độ Oxyz, cho bốn điểm A(1;-2;0), B(2;0;3),C(-2;1;3) và D(0;1;1). Tính \[\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\overrightarrow {AD} \].
Trả lời: ………………………………
Trong mặt phẳng tọa độ \(\left( P \right)\), cho phương trình tổng quát của mặt phẳng \(I\left( {a\,;\,b\,;\,c} \right)\). Tìm tọa độ một vectơ pháp tuyến của mặt phẳng \( \Rightarrow \).
Trả lời: ………………………………
Trong không gian \(Oxyz\), cho các vectơ \(\overrightarrow a = \left( { - 5;3; - 1} \right)\), \(\overrightarrow b = \left( {1;2;1} \right)\), \(\overrightarrow c = \left( {m;3; - 1} \right).\) Tìm giá trị của \(m\) sao cho \(\overrightarrow a = \left[ {\overrightarrow b ,\overrightarrow c } \right]\).
Trả lời: ………………………………
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\overrightarrow u = \left( {1;1;2} \right),\overrightarrow v = \left( { - 1;m;m - 2} \right)\]. Tìm giá trị của \(m\) sao cho \[\left| {\left[ {\overrightarrow u ,\overrightarrow v } \right]} \right| = \sqrt {14} \].
Trả lời: ………………………………
Trong hệ trục tọa độ Oxyz, cho A(0;1;-2),B(1;2;1),C(4;3;m). Tất cả giá trị của m để \[\left[ {\overrightarrow {OA} ,\overrightarrow {OB} } \right].\overrightarrow {OC} = 0\].
Trả lời: ………………………………
Trong không gian Oxyz, cho điểm M(-1;2;3) và mặt phẳng . Tính khoảng cách từ điểm Mđến mặt phẳng (P) .
Trả lời: ………………………………
Trong không gian Oxyz, điểm M thuộc trục Oy và cách đều hai mặt phẳng: (P): x+y-z+1=0 và (Q): x-y+z-5=0 có tọa độ bằng bao nhiêu?
Trả lời: ………………………………
Trong không gian với hệ trục tọa độ Oxyz, cho A(1;2;3), B(3;4;4). Tìm tất cả các giá trị của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng 2x+y+mz-1=0 bằng độ dài đoạn thẳng AB.
Trả lời: ………………………………
Tìm tọa độ điểm M trên trục Oy sao cho khoảng cách từ điểm M đến mặt phẳng Oy (P): 2x-y+3z-4=0 nhỏ nhất?
Trả lời: ………………………………
Tìm trên trục Oz điểm M cách đều điểm A(2;3;4)
và mặt phẳng (P):2x+3y+z-17=0.
Trả lời: ………………………………
Một công trình đang xây dựng được gắn hệ trục Oxyz (đơn vị trên mỗi trục tọa độ là mét). Ba bức tường (P),(Q),(R) (như hình vẽ) của tòa nhà lần lượt có phương trình: (P):x+2y-2z+1=0, (Q): 2x+y+2z-3=0,(R): 2x+4y-4z-19=0.

a) Hãy kiểm tính song song hoặc vuông góc giữa các bức tường (P),(Q),(R) của tòa nhà.
b) Tính khoảng giữa hai bức tường (P) và (Q) của tòa nhà.
Trả lời: ………………………………
Trong không gian Oxyz, cho mặt phẳng (P): 3x+4y-12z+5=0 và điểm A(2;4;-1) . Trên mặt phẳng (P) lấy điểm M . Gọi B là điểm sao cho . Tính khoảng cách B từ (P) đến mặt phẳng (P) .
Trả lời: ………………………………
Một công trình đang xây dựng được gắn hệ trục Oxyz (đơn vị trên mỗi trục tọa độ là mét). Ba bức tường (P),(Q),(T) (như hình vẽ) của tòa nhà lần lượt có phương trình: (P): 2x-y-z+1=0, (Q):x+3y-z-2=0,(R):4x-2y-2z+9=0,(T): 2x+6y-2z+15=0.

a) Hãy kiểm tính song song hoặc vuông góc giữa các bức tường (P),(Q),(T) của tòa nhà.
b) Tính khoảng giữa hai bức tường (Q) và (T) của tòa nhà.
c) Tính chiều rộng bức tường (Q)của tòa nhà.
Trả lời: ………………………………
Trong không gian Oxyz, cho mặt phẳng (P): 3x+4y-12z+5=0 và điểm A(2;4;-1) . Trên mặt phẳng (P) lấy điểm M . Gọi B là điểm sao cho . Tính khoảng cách B từ (P) đến mặt phẳng (P) .
Trả lời: ………………………………
Trong không gian Oxyz, cho hai mặt phẳng (P):2x+my+2mz-9=0 và (Q): 6x-y-z-10=0. Tìm m để (P) (Q) .
Trả lời: ………………………………
Trong không gian Oxyz, cho hai mặt phẳng (P): 5x+my+z-5=0 và (Q): nx-3y-2z+7=0. Tìm m,n để (P)//(Q) .
Trả lời: ………………………………
Trong không gian Oxyz, cho 3 điểm A(2;0;0), B(0;B;0),C(0;0;c) trong đó b.c 0 và mặt phẳng(P): y-z+1=0. Tìm mối liên hệ giữa b,c để mặt phẳng(ABC)vuông góc với mặt phẳng (P)
Trả lời: ………………………………
Trong không gian Oxyz, cho 3 điểm A(2;0;0), B(0;B;0),C(0;0;c) trong đó b.c 0 và mặt phẳng(P): y-z+1=0. Tìm mối liên hệ giữa b,c để mặt phẳng(ABC)vuông góc với mặt phẳng (P)
Trả lời: ………………………………
Trong không gian Oxyz, cho mặt phẳng (): ax-y+2z+b=0 đi qua giao tuyến của hai mặt phẳng (P): x-y-z+1=0 và (Q): x+2y+z-1=0 . Tính a+4b.
Trả lời: ………………………………
Trong không gian Oxyz, cho mặt phẳng (): ax-y+2z+b=0 đi qua giao tuyến của hai mặt phẳng (P): x-y-z+1=0 và (Q): x+2y+z-1=0 . Tính a+4b.
Trả lời: ………………………………
Gọi \(m,n\) là hai giá trị thực thỏa mãn giao tuyến của hai mặt phẳng \(\left( {{P_m}} \right):mx + 2y + nz + 1 = 0\) và \(\left( {{Q_m}} \right):x - my + nz + 2 = 0\) vuông góc với mặt phẳng \(\left( \alpha \right):4x - y - 6z + 3 = 0\). Tính \(m + n\).
Trả lời: ………………………………
Trong không gian 0xyz viết phương trình tổng quát mặt phẳng (P) đi qua điểm M ( 3;-1;4) đồng thời vuông góc với giá của vectơ .
Trả lời: ………………………………
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) qua \(M\left( {0; - 2;1} \right)\) và có cặp vectơ chỉ phương .
Trả lời: ………………………………
Trong không gian Oxyz, cho A(1;1;0), B(0;2;1), C(1;0;2), D(1;1;1). Mặt phẳng () đi qua A(1;1;0),B(0;2;1), ()song song với đường thẳng CD. Viết phương trình mặt phẳng ()
Trả lời: ………………………………
Trong không gian 0xyz, cho điểm M(2;1;-3) và mặt phẳng (P):3x-2y+z-3=0 . Viết phương trình của mặt phẳng đi qua M và song song với (P).
Trả lời: ………………………………
Trong không gian Oxyz, cho ba điểm A(3;-2;-2), B(3;2;0) ,C(0;2;1) . Viết phương trình mặt phẳng (ABC).
Trả lời: ………………………………
Trong không gian, cho hai điểm A(0;1;0) và B(2;1;3) . Viết phương trình mặt phẳng đi qua A và vuông góc với AB.
Trả lời: ………………………………
Trong không gian Oxyz, gọi M, N, P lần lượt là hình chiếu vuông góc của A(2;-3;1) lên các mặt phẳng tọa độ. Viết phương trình mặt phẳng ( MNP).
Trả lời: ………………………………
Một sân vận động được xây dựng theo mô hình là hình chóp cụt OAGD.BCFEcó hai đáy song song với nhau. Mặt sân OAGD là hình chữ nhật và được gắn hệ trục Oxyz như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân OAGD có chiều dài OA=100m , chiều rộng OD=60m và tọa độ điểm B(10;10;8).
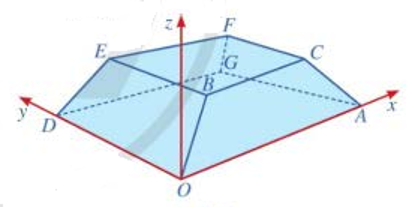
a) Lập phương trình mặt phẳng (OACB).
b) Tính khoảng cách từ điểm G đến mặt phẳng (OBED).
Trả lời: ………………………………
Cho hình lập phương ABCD,A'B'C'D' có độ dài cạnh bằng 1. Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,C'D',DD'. Chọn hệ tọa độ Oxyz như hình vẽ, xác định tọa độ các điểm M,N,P,Q.
a) Lập phương trình mặt phẳng (A'BC') .
b) Tính khoảng cách từ điểm Q đến mặt phẳng (MNP/0 .
c) Tính khoảng giữa hai mặt phẳng (A'BC') và mặt phẳng (ACD').
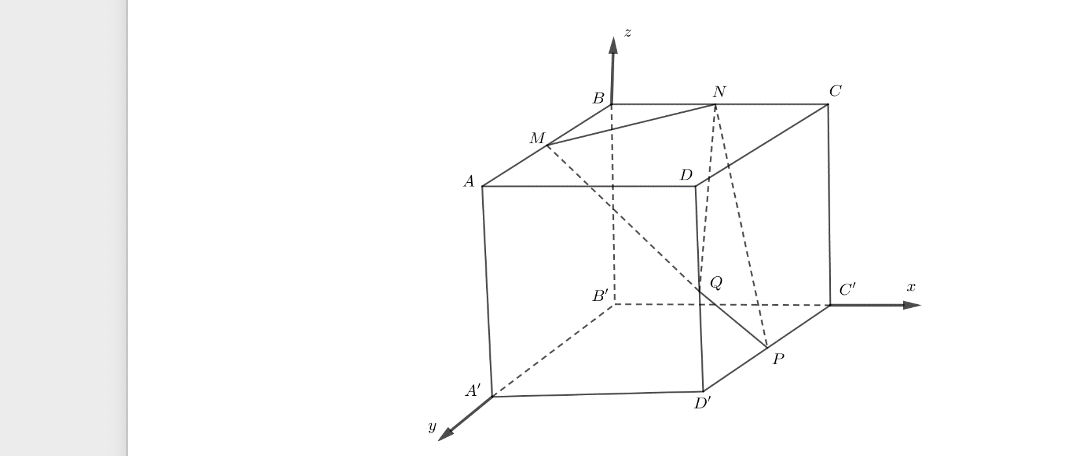
Trả lời: ………………………………
Cho hình chóp S.ABC có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng với đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Chọn hệ tọa độ Oxyz như hình vẽ dưới.
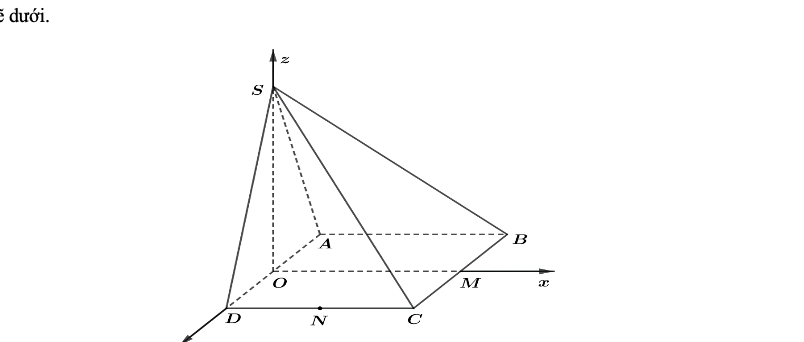
a) Lập phương trình mặt phẳng (SOM)A .
b) Tính khoảng cách từ điểm A đến mặt phẳng (SBC) .
c) Gọi Q là trung điểm SD. Tính khoảng giữa hai mặt phẳng (SAC) và mặt phẳng (ONQ).
Trả lời: ………………………………
Cho tứ diện \[OABC\], có \[OA,OB,OC\]đôi một vuông góc và \[OA = 5,OB = 2,OC = 4\]. Gọi \[M,N\] lần lượt là trung điểm của \[OB\]và \[OC\]. Gọi G,K lần lượt là trọng tâm của tam giác \[ABC\] và AMN . Chọn hệ tọa độ Oxyz như hình vẽ dưới.
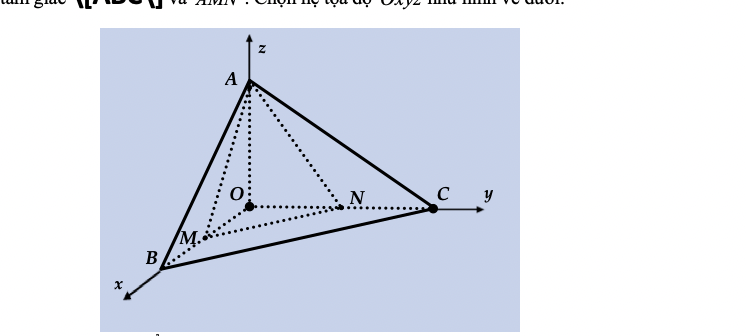
a) Lập phương trình mặt phẳng (ABC) .
b) Tính khoảng cách từ điểm B đến mặt phẳng (SMN) .
Cho hình chóp \[S.ABCD\] đáy là hình thang vuông tại \[A\] và \(D\), \[SA \bot \left( {ABCD} \right)\]. Góc giữa \(SB\) và mặt phẳng đáy bằng \({45^{\rm{o}}}\), \(E\) là trung điểm của \[SD\], \(AB = 2a\), \(AD = DC = a\). Gọi G là trọng tâm của tam giác ACE . Chọn hệ tọa độ Oxyz như hình vẽ dưới.
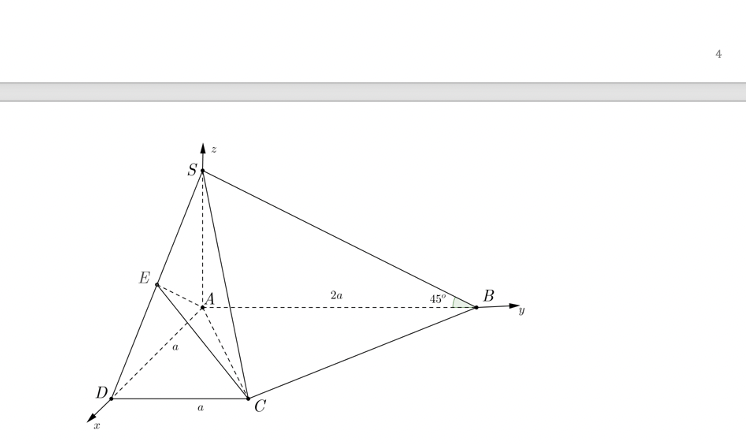
a) Lập phương trình mặt phẳng (SAC) .
b) Tính khoảng cách từ điểm B đến mặt phẳng (AEC) .
Trả lời: ………………………………
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm S(-1;6;2),A(0;0;6) , B(0;3;0), C(-2;0;0). Gọi H là chân đường cao vẽ từ S của tứ diện S.ABC . Lập phương trình mặt phẳng đi qua ba điểm S, B, H .
Trả lời: ………………………………
Trong không gian với hệ tọa độ \(Oxyz\), cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình chữ nhật. Biết \(A\left( {0;0;0} \right)\),\(D\left( {2;0;0} \right)\),\(B\left( {0;4;0} \right)\),\(S\left( {0;0;4} \right)\). Gọi M là trung điểm của \(SB\) và G là trọng tâm của tam giác SCD .
a) Lập phương trình mặt phẳng (AMC) .
b) Tính khoảng cách từ điểm B đến mặt phẳng (AMG)
Trả lời: ………………………………
Cho hình hộp chữ nhật ABCD.A'B'C'D' có các kích thước AB=4,AD=3,AA'=5. Gọi G là trọng tâm của tam giác ACB' .
a) Tính độ dài cạnh GD' .
b) Tính khoảng cách từ điểm G đến mặt phẳng (AB'C) .
c) Tính khoảng giữa hai mặt phẳng (AB'D') và mặt phẳng (CB'D').
Trả lời: ………………………………
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau và AD=2,AB=AC=1. Gọi I là trung điểm của đoạn thẳng BC và G là trọng tâm của tam giác ABD.
a) Tính độ dài cạnh IG .
b) Tính khoảng cách từ điểm C đến mặt phẳng (AIG) .
Trả lời: ………………………………
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA=a và vuông góc với mặt phẳng đáy. Gọi M,N lần lượt là trung điểm của SB và SD và G là trọng tâm của tam giác AMN .
a) Tính tọa độ điểm G.
b) Tính khoảng cách từ điểm G đến mặt phẳng (SBC) .
c) Tính khoảng cách từ điểm C đến mặt phẳng (AMN) .
Trả lời: ………………………………
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a,BC= , SA=a và vuông góc với đáy ABCD . Gọi G là trọng tâm của tam giác SBD.
a) Tính khoảng cách từ điểm C đến mặt phẳng (SBD) .
b) Tính khoảng cách từ điểm G đến mặt phẳng (SCD) .
Trả lời: ………………………………
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm I, có độ dài đường chéo bằng a và SA vuông góc với mặt phẳng (ABCD) . Gọi là góc giữa hai mặt phẳng (SBD) và (ABCD) và .
a) Tính khoảng cách từ điểm I đến mặt phẳng (SAB) .
b) Tính khoảng cách từ điểm I đến mặt phẳng (SCD) .
Trả lời: ………………………………
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M,N lần lượt là trung điểm của SC,SD.
a) Tính khoảng cách từ điểm A đến mặt phẳng (SBD) .
b) Tính khoảng cách từ điểm S đến mặt phẳng (GMN) .
Trả lời: ………………………………








