23 bài tập Khoảng cách từ một điểm đến một mặt phẳng (có lời giải)
23 câu hỏi
Tính khoảng cách từ điểm \(M(1;2;3)\) đến các mặt phẳng sau:
a) \((P):x + y + z + 12 = 0\); b) \((Q):4x + 3y + 10 = 0\).
Tính chiều cao của hình chóp S.ABC có toạ độ các đỉnh là \(S(5;0;1),A(1;1;1)\), \(B(2;3;4),C(5;2;3)\).
Tính khoàng cách giữa hai mặt phẳng song song \((P)\) và \((Q)\) cho bởi các phương trình sau đây: \((P):2x + y + 2z + 9 = 0{\rm{; }}\)\((Q):\)2 x+y+2 z+99=0.
a) Tính chiều cao của hình chóp O.MNP với toạ độ các đình là \(O(0;0;0),M(2;1;2)\), \(N(3;3;3),P(4;5;6)\).
b) Tính khoảng cách giữa hai mặt phẳng song song \((R):8x + 6y + 70 = 0\) và (S): \(16x + 12y - 2 = 0\).
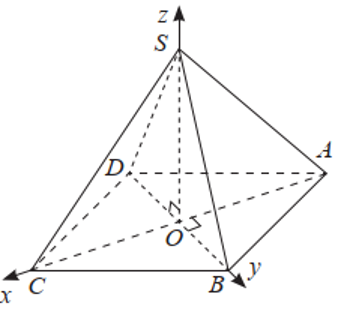
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(a\sqrt 2 \), chiều cao bằng 2a và \(O\) là tâm của đáy. Bằng cách thiết lập hệ trục toạ độ Oxyz như Hình vẽ, tính khoảng cách từ điểm \(C\) đến mặt phẳng \((SAB)\).
Tính khoảng cách từ gốc toạ độ và từ điểm \(M(1; - 2;13)\) đến mặt phẳng \((P):2x - 2y - z + 3 = 0\).
Cho mặt phẳng \((P):2x - 3y + 6z - 7 = 0\) và điểm \(M(5;2; - 3)\). Tính khoảng cách từ điểm \(M\) đến mặt phẳng \((P)\).
Tính khoàng cách giữa hai mă̆t phẳng song song \((P):x - 2 = 0\) và \((Q):x - 8 = 0\).
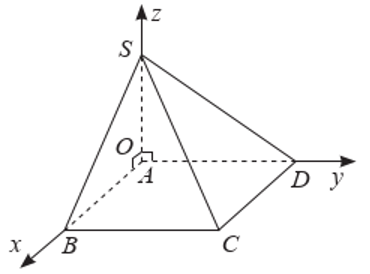
Cho hình chóp \(S \cdot ABCD\) có đáy ABCD là hình chữ nhật với \(AB = 2a,AD = 5a,SA = 3a\) và \(SA \bot (ABCD)\). Bằng cách thiết lập hệ trục toạ độ Oxyz như Hình vẽ, tính khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\).
Cho điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\). Tính khoảng cách từ \(M\) đến các mặt phẳng \(x - a = 0\), \(y - b = 0,z - c = 0\).
Cho hai mă̆t phẳng \(\left( {{P_1}} \right):x + 2y - 3z + 5 = 0\) và \(\left( {{P_2}} \right): - 4x - 8y + 12z + 3 = 0\).
a) Chứng minh rằng \(\left( {{P_1}} \right)//\left( {{P_2}} \right)\).
b) Tính khoảng cách giữa hai mặt phẳng \(\left( {{P_1}} \right),\left( {{P_2}} \right)\).
Cho mặt phẳng \((P):2x - 2y - z + 3 = 0\) và điểm \({M_0}(3;1; - 5)\). Tính khoảng cách từ điểm \({M_0}\) đến mặt phẳng \((P)\).
Cho mặt phẳng \(\left( {{P_1}} \right):2x - 4y - 4z + 3 = 0\) và mặt phẳng \(\left( {{P_2}} \right):x - 2y - 2z + 1 = 0\).
a) Chứng minh rằng \(\left( {{P_1}} \right)//\left( {{P_2}} \right)\).
b) Tính khoảng cách giữa hai mặt phẳng song song \(\left( {{P_1}} \right),\left( {{P_2}} \right)\).
Trong không gian Oxyz, tính khoảng cách từ gốc tọa độ đến mặt phẳng \((P):2x + 2y - z + 1 = 0\).
Trong không gian Oxyz, tính khoảng cách từ điểm \(M(1;2; - 1)\) đến mặt phẳng \((P):x + 2y - 2z + 5 = 0\).
Trong không gian Oxyz , cho hai mặt phẳng \((P):x + y + z + 2 = 0,(Q):x + y + z + 6 = 0\). Chứng minh rằng hai mặt phẳng đã cho song song với nhau và tính khoảng cách giữa hai mặt phẳng đó.
Trong không gian Oxyz, cho hai mặt phẳng \((P):x + 3y + z + 2 = 0\) và \((Q):x + 3y + z + 5 = 0\).
a) Chứng minh rằng \((P)\) và \((Q)\) song song với nhau.
b) Lấy một điểm thuộc \((P)\), tính khoảng cách từ điểm đó đến \((Q)\). Từ đó tính khoảng cách giữa hai mặt phẳng \((P)\) và \((Q)\).
Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) : \(2x + 3y - 6z - 7 = 0,(\beta ):2x + 3y - 6z + 14 = 0\).
a) Tính khoảng cách từ gốc toạ độ và từ điểm \(M(1; - 2;3)\) đến \((\alpha )\).
b) Chứng minh \((\alpha )//(\beta )\) và tính khoảng cách giữa hai mặt phẳng \((\alpha )\) và \((\beta )\).
Trong không gian Oxyz, cho hai mặt phẳng (P): \(x + 3y - z = 0,(Q):x - y - 2z + 1 = 0\).
a) Chứng minh rằng hai mặt phẳng \(({\rm{P}})\) và \(({\rm{Q}})\) vuông góc với nhau.
b) Tim điểm M thuộc trục Ox và cách đều hai mặt phẳng \(({\rm{P}})\) và \(({\rm{Q}})\).
Cho hình chóp S.ABC thoả mãn . Gọi \(H\) là hình chiếu vuông góc của \(S\) trên mặt phẳng \((ABC)\). Chứng minh rằng
\(\frac{1}{{S{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} + \frac{1}{{S{C^2}}}{\rm{. }}\)
Cho bốn điểm \(A(1;0;0),B(0;2;0),C(0;0;3)\) và \(D(1;2;3)\). Chứng minh rằng A, B, C, D không đồng phẳng.
Cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(AB = 2a,AD = 3a,A{A^\prime } = 4a(a > 0)\). Gọi M, N, P lần lượt là các điểm thuộc các tia \(AB,AD,A{A^\prime }\) sao cho \(AM = a\), \(AN = 2a,AP = 3a\). Tính khoảng cách từ điểm \({C^\prime }\) đến mặt phẳng \((MNP)\).
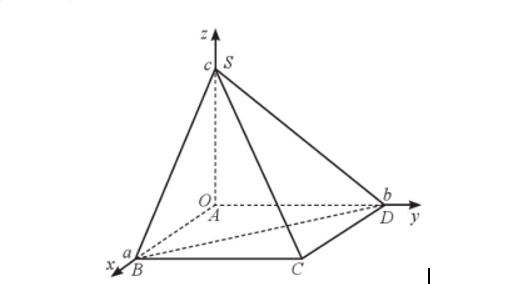
Trong không gian với hệ toạ độ Oxyz, cho hình chóp S.ABCD có đáy là hình chữ nhật và các điểm \(A(0;0;0),B(a;0;0)\), \(D(0;b;0),S(0;0;c)\) với a, b, c là các số dương (Hinh vẽ ).
a) Tìm toạ độ của điểm \(C\), trung điểm \(M\) của BC, trọng tâm \(G\) của tam giác SCD.
b) Lâp phương trình mặt phẳng (SBD).
c) Tính khoảng cách từ điểm G đến mặt phẳng (SBD).
