20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 1. Phương trình mặt phẳng (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong không gian Oxyz, tọa độ một vectơ \(\overrightarrow n \) vuông góc với cả hai vectơ \(\overrightarrow a = \left( {1;1; - 2} \right),\overrightarrow b = \left( {1;0;3} \right)\) là
(3; −5; −1).
(2; 3; −1).
(3; 5; −2).
(2; −3; −1).
Trong không gian tọa độ Oxyz, mặt phẳng \(\left( \alpha \right):x - 2y - z + 5 = 0\)song song với mặt phẳng nào dưới đây?
\(\left( {{\beta _2}} \right):2x - 4y - 2z + 7 = 0\).
\(\left( {{\beta _1}} \right):3x + y + z - 3 = 0\).
\(\left( {{\beta _3}} \right):2x - 4y - 2z + 10 = 0\).
\(\left( {{\beta _4}} \right): - 2x + 4y - 2z - 7 = 0\).
Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng \(\frac{x}{{ - 2}} + \frac{y}{{ - 1}} + \frac{z}{3} = 1\) là
\(\overrightarrow n = \left( { - 3; - 6; - 2} \right)\).
\(\overrightarrow n = \left( { - 2; - 1;3} \right)\).
\(\overrightarrow n = \left( {2; - 1;3} \right)\).
\(\overrightarrow n = \left( {3;6; - 2} \right)\).
Trong không gian Oxyz, cho ba điểm A(3; 0; 0), B(0; 4; 0), C(0; 0; 5). Phương trình chính tắc của mặt phẳng (ABC) là
\(\frac{x}{3} + \frac{y}{4} + \frac{z}{5} = 1\).
\(\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\).
\(\frac{x}{3} + \frac{y}{4} - \frac{z}{5} = 1\).
\(\frac{x}{3} - \frac{y}{4} - \frac{z}{5} = 1\).
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình \( - 2x + 2y - z - 3 = 0\). Mặt phẳng (P) có vectơ pháp tuyến là
\(\overrightarrow {{n_1}} = \left( {4; - 4;2} \right)\).
\(\overrightarrow {{n_2}} = \left( { - 2;2; - 3} \right)\)
\(\overrightarrow {{n_3}} = \left( { - 4;4;2} \right)\).
\(\overrightarrow {{n_4}} = \left( {0;0; - 3} \right)\).
Trong không gian Oxyz, cho mặt phẳng (P): 2x + y – 2z + 4 = 0. Mặt phẳng nào sau đây vuông góc với (P)?
\(2x + y - 2z + 5 = 0\).
\(x + 2y + 2z - 5 = 0\).
\(x + 3y - z + 1 = 0\).
\(x + y + z - 6 = 0\).
Trong không gian Oxyz, cho mặt phẳng (P): \(x + y + z - 3 = 0\)đi qua điểm nào dưới đây:
\(M\left( { - 1; - 1; - 1} \right)\).
\(N\left( {1;1;1} \right)\).
\(P\left( { - 3;0;0} \right)\).
\(Q\left( {0;0; - 3} \right)\).
Trong không gian Oxyz, khoảng cách từ M(1; 2; −3) đến (P): x + 2y + 2z – 10 = 0 là
\(3\).
\(\frac{2}{3}\).
\(\frac{4}{3}\).
\(\frac{{11}}{3}\).
Trong không gian Oxyz, cho ba điểm \(A\left( {3; - 2; - 2} \right),B\left( {3;2;0} \right),C\left( {0;2;1} \right)\). Phương tình mặt phẳng (ABC) là
\(2x - 3y + 6z + 12 = 0\).
\(2x + 3y - 6z - 12 = 0\).
\(2x - 3y + 6z = 0\).
\(2x + 3y + 6z + 12 = 0\).
Trong không gian Oxyz, cho hai điểm A(2; 4; 1), B(−1; 1; 3) và mặt phẳng (P): x – 3y + 2z – 5 = 0. Lập phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P).
\(2y + 3z - 11 = 0\).
\(2x - 3y - 11 = 0\).
\(x - 2y + 2z - 5 = 0\).
\(3y + 2z - 11 = 0\).
Trong không gian Oxyz, cho hai điểm A(1; 0; 0), B(4; 1; 2).
(a) \(\overrightarrow {AB} = \left( {3;1;2} \right)\).
(b) Mặt phẳng đi qua A và vuông góc với AB có phương trình là \(3x + y + 2z - 3 = 0\).
(c) Nếu I là trung điểm đoạn thẳng AB thì \(I\left( {\frac{5}{2};\frac{1}{2};1} \right)\).
(d) Mặt phẳng trung trực đoạn thẳng AB có phương trình là \(3x + y + 2z - 12 = 0\).
Trong không gian Oxyz, cho mặt phẳng (P): 3x + y – z – 12 = 0.
(a) Mặt phẳng (P) có một vectơ pháp tuyến là \(\overrightarrow n = \left( {3;1; - 1} \right)\).
( b) Mặt phẳng (P) đi qua điểm A(5; 3; −6).
( c) Cho điểm M(a; b; 1) thuộc mặt phẳng (P). Khi đó 3a + b = −13.
(d) (P) cắt trục Ox tại A, cắt trục Oz tại B. Diện tích tam giác OAB bằng 12.
a) Trong không gian Oxyz, cho \(M\left( { - 2; - 4;3} \right)\) và \(\left( P \right):2x - y + 2z - 3 = 0\), \(\left( Q \right):2x - y + 2z - 6 = 0\).
( a) \(d\left( {M,\left( P \right)} \right) = 2\).
(b) M cách đều hai mặt phẳng (P) và (Q).
(c) \(d\left( {\left( P \right),\left( Q \right)} \right) = 1\).
(d) (α) song song và cách (Q) một khoảng bằng 2 có phương trình là \(\left( \alpha \right):2x - y + 2z - 9 = 0\).
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 2; 0), B(1; 0; 2), C(2; 1; 3) và mặt phẳng (P): x – y + 2z + 7 = 0.
(a) Mặt phẳng (ABC) có một vectơ pháp tuyến là (2; 1; 1).
(b) Mặt phẳng (ABC) đi qua điểm M(3; 1; 5).
(c) Mặt phẳng (ABC) vuông góc với mặt phẳng (P).
(d) Khoảng cách từ điểm A đến mặt phẳng (P) bằng 6.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 1; 2), B(2; −2; 1), C(−2; 1; 0). Gọi (P) là mặt phẳng đi qua ba điểm A, B, C.
(a) Một vectơ pháp tuyến của mặt phẳng (P) là \(\overrightarrow n = \left( {1;1;1} \right)\).
(b) Phương trình mặt phẳng (P) là \(x + y - z + 1 = 0\).
(c) Mặt phẳng (P) cắt trục Ox tại điểm M(−1; 0; 0).
(d) Điểm \(N\left( {1; - 2;0} \right)\) thuộc mặt phẳng (P).
Trong không gian Oxyz, cho hai điểm A(1; 2; 0), B(3; 4; −2) và (P): x – y + z – 4 = 0. Phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có dạng: ax + by + cz + 2 = 0. Tính \(a + b + c\).
Trong không gian Oxyz, cho điểm M(1; 4; 9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O) sao cho OA + OB + OC đạt giá trị nhỏ nhất. Tính khoảng cách d từ gốc tọa độ O đến mặt phẳng (P). (kết quả làm tròn đến hàng phần trăm).
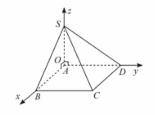
Cho hình chóp S.ABCD có cạnh bên SA vuông góc với đáy, tứ giác ABCD là hình vuông, SA = 3, AB = 2. Bằng cách thiết lập hệ trục tọa độ Oxyz như hình vẽ, tính khoảng cách từ điểm A đến mặt phẳng (SCD) (làm tròn kết quả đến hàng phần trăm).
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 1; −1) và mặt phẳng (P): \(ax - 3y - z - 8 = 0\) (với a là hằng số). Biết rằng mặt phẳng (P) đi qua điểm M. Giá trị của a bằng bao nhiêu?
Trong không gian Oxyz, một ngôi nhà như hình vẽ dưới đây có sàn nhà nằm trên mặt phẳng (Oxy). Hai mái nhà lần lượt nằm trên các mặt phẳng (P): \(x - 2y + 5 = 0\) và \(\left( Q \right):x - 2y - 3z + 20 = 0\). Hỏi là chiều cao của ngôi nhà tính từ sàn nhà lên nóc nhà là bao nhiêu? (làm tròn đến hàng đơn vị).









