Quiz

ĐGTD ĐH Bách khoa - Tư duy Toán học - Bất phương trình logarit

VietJackĐH Bách KhoaĐánh giá năng lực15 lượt thi

Bắt đầu ngay

25 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Giải bất phương trình $\log_{\frac{1}{3}} (x + 9^{500}) > - 1000$

x < 0

$x > - 9^{500}$

x > 0

$- 3^{1000} < x < 0$

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Giải bất phương trình $\log_{2} (3 x - 1) \geq 3$

$x \geq 3$

$\frac{1}{3} < x < 3$

x < 3

$x \geq \frac{10}{3}$

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập nghiệm S của bất phương trình $\log_{\frac{1}{2}} (x - 1) > \log_{\frac{1}{2}} (5 - 2 x)$

$S = (- \infty; 2)$

$S = (2; \frac{5}{2})$

$S = (\frac{5}{2}; + \infty)$

S = (1;2)

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Giải bất phương trình $\log_{3} (2^{x} - 3) < 0$

0 < x < 2

x < 2

$l o g_{2} 3 < x < 2$

x > 2

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập hợp nghiệm S của bất phương trình: $l o g_{\frac{π}{4}} (x^{2} + 1) < l o g_{\frac{π}{4}} (2 x + 4)$

S = (-2;-1)

$S = (- 2; + \infty)$

$S = (3; + \infty) \cup (- 2; - 1)$

$S = (3; + \infty)$

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của phương trình $\log_{3} (\log_{\frac{1}{2}} x) < 1$ là

(0;1)

$(\frac{1}{8}; 1)$

(1;8)

$(\frac{1}{8}; 3)$

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Số nguyên nhỏ nhất thỏa mãn $\log_{2} (5 x - 3) > 5$ là:

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $\ln [(x - 1) (x - 2) (x - 3) + 1] > 0$ là:

$(1; 2) \cup (3; + \infty)$

$(- \infty; 1) \cup (2; 3)$

$(1; 2) \cap (3; + \infty)$

$(- \infty; 1) \cap (2; 3)$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $\log (x^{2} + 25) > \log (10 x)$ là:

R\{5}

$(0; 5) \cup (5; + \infty)$

$(0; + \infty)$

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Nghiệm của bất phương trình $\log_{2} (x + 1) + \log_{\frac{1}{2}} \sqrt{x + 1} \leq 0$ là :

$- 1 \leq x \leq 0$

$- 1 < x \leq 0$

$- 1 < x \leq 1$

$x \leq 0$

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Giải bất phương trình $\log_{0,7} (\log_{6} \frac{x^{2} + x}{x + 4}) < 0$

$(- 4; - 3) \cup (8; + \infty)$

(-4;-3)

$(- 4; + \infty)$

$(8; + \infty)$

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Xác định tập nghiệm S của bất phương trình $\ln x^{2} > \ln (4 x - 4)$

$S = (1; + \infty) ∖ {2}$

R\{2}

$(2; + \infty)$

$(1; + \infty)$

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Giải bất phương trình: $\log_{2}^{2} x - 4033 \log_{2} x + 4066272 \leq 0$

[2016; 2017]

(2016; 2017)

$[2^{2016}; 2^{2017}]$

$[2^{2016}; + \infty)$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $2017 \log_{2} x \leq 4^{\log_{2} 9}$ là

$0 < x \leq 8^{2017}$

$0 < x \leq \sqrt[2017]{2^{81}}$

$0 \leq x \leq 9^{2017}$

$0 < x \leq \sqrt[2017]{9}$

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $\log_{\frac{2}{3}} (3 x - 2) > \log_{\frac{2}{3}} (2 x + 1)$ là

$(\frac{2}{3}; 3)$

$(3; + \infty)$

$(- \infty; 3)$

$(\frac{2}{3}; 2)$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tất cả các giá trị thực của tham số m để bất phương trình $4. {(\log_{2} \sqrt{x})}^{2} + \log_{2} x + m \geq 0$ nghiệm đúng với mọi giá trị $x \in [1; 64]$

m < 0

$m \leq 0$

$m \geq 0$

m > 0

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $(2^{x^{2} - 4} - 1) . \ln x^{2} < 0$ là:

{1;2}

$(- 2; - 1) \cup (1; 2)$

(1;2)

[1;2]

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Với m là tham số thực dương khác 1. Hãy tìm tập nghiệm S của bất phương trình $\log_{m} ({2.1}^{2} + 1 + 3) \leq \log_{m} ({3.1}^{2} - 1) \Leftrightarrow \log_{m} 6 \leq \log_{m} 2 \Leftrightarrow 0 m < 1$ . Biết rằng x = 1 là một nghiệm của bất phương trình.

$S = (- 2; 0) \cup (\frac{1}{3}; 3]$

$S = (- 1; 0) \cup (\frac{1}{3}; 2]$

$S = [- 1, 0) \cup (\frac{1}{3}; 3]$

$S = (- 1; 0) \cup (1; 3]$

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập nghiệm S của bất phương trình $\log_{\frac{1}{2}} (x + 2) - \log_{\frac{1}{\sqrt{2}}} (x) > \log_{2} (x^{2} - x) - 1$

$S = (2; + \infty)$

S = (1;2)

S = (0;2)

S = (1;2]

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $\log_{3} x \leq \log_{\frac{1}{3}} (2 x)$ là nửa khoảng (a;b]. Giá trị của $a^{2} + b^{2}$ bằng

$\frac{1}{2}$

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $9^{\log_{9}^{2} x} + x^{\log_{9} x} \leq 18$ là:

[1;9]

$[\frac{1}{9}; 9]$

$(0; 1] \cup [9; + \infty)$

$(0; \frac{1}{9}] \cup [9; + \infty)$

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập nghiệm của bất phương trình $\log_{2} (x \sqrt{x^{2} + 2} + 4 - x^{2}) + 2 x + \sqrt{x^{2} + 2} \leq 1 là (- \sqrt{a}; - \sqrt{b})$ .Khi đó ab bằng

$\frac{12}{5}$

$\frac{5}{12}$

$\frac{15}{16}$

$\frac{16}{15}$

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

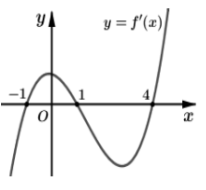
Cho hàm số f(x) liên tục trên R và có đồ thị f′(x) như hình vẽ bên. Bất phương trình $\log_{5} [f (x) + m + 2] + f (x) > 4 - m$ đúng với mọi $x \in (- 1; 4)$ khi và chỉ khi Media VietJack

$m \geq 4 - f (- 1)$

$m \geq 3 - f (1)$

$m < 4 - f (- 1)$

$m \geq 3 - f (4)$

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho phương trình $\log_{7} (x^{2} + 2 x + 2) + 1 > \log_{7} (x^{2} + 6 x + 5 + m)$ . Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình trên có tập nghiệm chứa khoảng (1;3)?

Vô số

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

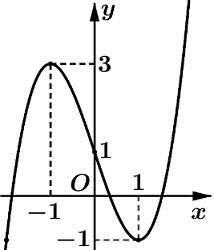
Cho hàm số y = f(x). Hàm số y = f′(x) có đồ thị như hình bên. Biết $f (- 1) = 1, f (- \frac{1}{e}) = 2.$ . Tìm tất cả các giá trị của m để bất phương trình $f (x) < l n (- x) + m$ nghiệm đúng với mọi $x \in (- 1; - \frac{1}{e}) .$ Media VietJack