12 câu hỏi
Cho hàm số \(f\left( x \right) = 3 + \frac{1}{x}\). Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của \(f\left( x \right)\) trên \(\left( {0; + \infty } \right)\)?
\({F_1}\left( x \right) = 3x - \frac{1}{{{x^2}}}\).
\({F_2}\left( x \right) = 3x + \ln x\).
\({F_3}\left( x \right) = 3x + \frac{1}{{{x^2}}}\).
\({F_4}\left( x \right) = 3x - \ln x\).
Biết \(F\left( x \right) = {x^3}\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\). Giá trị của \(\int\limits_1^2 {\left( {2 + f\left( x \right)} \right)dx} \) bằng
\(7\).
\(9\).
\(\frac{{15}}{4}\).
\(\frac{{23}}{4}\).
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f\left( a \right) = 2,f\left( b \right) = - 4\). Tính \(T = \int\limits_a^b {f'\left( x \right)dx} \).
\(T = - 6\).
\(T = 2\).
\(T = 6\).
\(T = - 2\).
Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = {x^2},y = x\) và các đường thẳng \(x = 0;x = 1\) được tính bởi công thức
\(S = \int\limits_{ - 1}^0 {\left| {{x^2} - x} \right|} dx\).
\(S = \int\limits_0^1 {\left| {{x^2} + x} \right|} dx\).
\(S = \int\limits_{ - 1}^0 {\left| {{x^2} + x} \right|} dx\).
\(S = \int\limits_0^1 {\left| {{x^2} - x} \right|} dx\).
Tính \(I = \int\limits_0^1 {\left( {\frac{1}{{2x + 1}} + 3\sqrt x } \right)} dx\).
\(2 + \ln \sqrt 3 \).
\(4 + \ln 3\).
\(2 + \ln 3\).
\(1 + \ln \sqrt 3 \).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \({S_1};{S_2}\) là diện tích của hình phẳng tương ứng như trong hình vẽ. Biết \({S_1} = 4\) và \({S_2} = \frac{4}{3}\). Tính \(\int\limits_1^6 {f\left( x \right)dx} \).
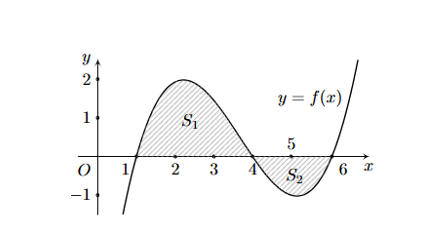
\(I = \frac{{11}}{3}\).
\(I = \frac{{16}}{3}\).
\(I = \frac{8}{3}\).
\(I = \frac{{10}}{3}\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x - 2y - 3z + 1 = 0\). Hỏi vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\)?
\(\left( {1; - 2; - 3} \right)\).
\(\left( {1;2;3} \right)\).
\(\left( { - 2;3;1} \right)\).
\(\left( {2; - 2;4} \right)\).
Trong không gian\[Oxyz\], mặt phẳng \[\left( \alpha \right):x - y + 2z - 3 = 0\]đi qua điểm nào dưới đây?
\[M\left( {1;1;\frac{3}{2}} \right)\].
\[N\left( {1; - 1; - \frac{3}{2}} \right)\].
\[P\left( {1;6;1} \right)\].
\[Q\left( {0;3;0} \right)\].
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;0;0} \right),B\left( {0;1;0} \right),C\left( {0;0; - 2} \right)\). Mặt phẳng \(\left( {ABC} \right)\) có phương trình là:
\(\frac{x}{3} + \frac{y}{{ - 1}} + \frac{z}{2} = 1\).
\(\frac{x}{3} + \frac{y}{1} + \frac{z}{{ - 2}} = 1\).
\(\frac{x}{3} + \frac{y}{1} + \frac{z}{2} = 1\).
\(\frac{x}{{ - 3}} + \frac{y}{1} + \frac{z}{2} = 1\).
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {0;0;1} \right),B\left( {1;2;3} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là
\(x + 2y + 2z - 11 = 0\).
\(x + 2y + 2z - 2 = 0\).
\(x + 2y + 4z - 4 = 0\).
\(x + 2y + 4z - 17 = 0\).
Trong không gian \[Oxyz\], khoảng cách giữa hai mặt phẳng \[\left( P \right):x + 2y + 2z - 8 = 0\]và \[\left( Q \right):x + 2y + 2z - 4 = 0\] bằng
1.
\[\frac{4}{3}\].
2.
\[\frac{7}{3}\].
Trong không gian \[Oxyz\], cho ba điểm \[A\left( {2;0;0} \right)\], \[B\left( {0;3;0} \right)\], \[C\left( {0;0; - 1} \right)\]. Phương trình của mặt phẳng \[\left( P \right)\] qua \[D\left( {1;1;1} \right)\]và song song với mặt phẳng \[\left( {ABC} \right)\] là
\[2x + 3y - 6z + 1 = 0\].
\[3x + 2y - 6z + 1 = 0\].
\[3x + 2y - 5z = 0\].
\[6x + 2y - 3z - 5 = 0\].
