Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
39 câu hỏi
Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x
x + 3y = 7;
x2 + y2 = 5;
\(y = \sqrt {{x^2} - 2} \);
\(y = \frac{2}{x}\).
Cho hàm số dưới dạng bảng như sau:
x | 1 | 2 | 3 | 4 | 5 |
y | 1 | 3 | 5 | 7 | 9 |
Giá trị của hàm số y tại x = 3 là
2
3
5
7
Cho hàm số y = f(x) có đồ thị như hình dưới.
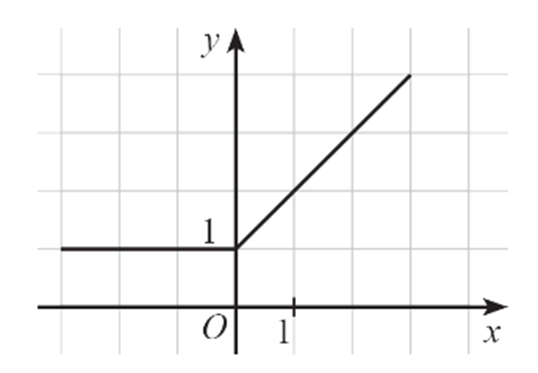
Hàm số trên đồng biến trên khoảng
(0; 1);
(1; + ∞);
(0; + ∞);
(– ∞; 0).
Hàm số \(y = \frac{{x + 2}}{{{x^2} - 3x + 2}}\) có tập xác định là
(1; 2);
[1; 2];
{1; 2};
ℝ \ {1; 2}.
Cho hàm số \(y = 2\sqrt {{x^2} - 5x} \). Giá trị của hàm số tại x = 10 là
20;
\(10\sqrt 2 \);
\[2\sqrt {10} \];
Không tồn tại.
Trong các hàm số sau, hàm số nào không phải là hàm số bậc hai?
y = x2 – 5x + 3;
y = 1 – 2x2 + 4x;
y = x(x2 + x + 1);
y = 7 – x2.
Cho hàm số bậc hai y = 2x2 + 3x – 8. Hoành độ đỉnh của đồ thị hàm số bậc hai này là
\( - \frac{3}{4}\);
\(\frac{3}{4}\);
\(\frac{3}{2}\);
\( - \frac{3}{2}\).
Hàm số bậc hai y = 2 – 3x2 + 4x có hệ số tự do là
2;
– 3;
4;
– 2.
Cho hàm số bậc hai f(x) = 2x2 – 8x + 7. Phát biểu nào sau đây là đúng?
Hàm số đồng biến trên khoảng (– ∞; 2), nghịch biến trên khoảng (2; + ∞);
Hàm số đồng biến trên khoảng (– ∞; 4), nghịch biến trên khoảng (4; + ∞);
Hàm số đồng biến trên khoảng (4; + ∞), nghịch biến trên khoảng (– ∞; 4);
Hàm số đồng biến trên khoảng (2; + ∞), nghịch biến trên khoảng (– ∞; 2).
Xác định parabol y = ax2 + c, biết rằng parabol này đi qua hai điểm A(1; 1) và B(2; – 2).
y = – x2 + 2;
y = x2 + 2;
y = 2x2 – 1;
y = 2x2 + 1.
Tìm khẳng định đúng trong các khẳng định sau.
f(x) = 3x2 + x – 4 là tam thức bậc hai;
f(x) = 3x – 5 là tam thức bậc hai;
f(x) = 2x3 + 3x – 2 là tam thức bậc hai;
f(x) = (x2)2 – x2 + 3 là tam thức bậc hai.
Cho hàm số f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Cho biết dấu của ∆ khi f(x) luôn cùng dấu với hệ số a với mọi x ∈ ℝ.
∆ ≤ 0;
∆ = 0;
∆ > 0;
∆ < 0.
Cho tam thức f(x) = x2 – 8x + 16. Khẳng định nào sau đây là đúng?
Phương trình f(x) = 0 vô nghiệm;
f(x) > 0 với mọi x ∈ ℝ;
f(x) ≥ 0 với mọi x ∈ ℝ;
f(x) < 0 khi x < 4.
Trong các phát biểu sau, phát biểu nào sai?
x2 – 3x + 2 > 0 khi x ∈ (– ∞; 1) ∪ (2; + ∞);
x2 – 3x + 2 ≤ 0 khi x ∈ [1; 2];
x2 – 3x + 2 < 0 khi x ∈ [1; 2);
x2 – 3x + 2 ≥ 0 khi x ∈ (– ∞; 1] ∪ [2; + ∞).
Tập nghiệm của bất phương trình x2 – 7x + 10 < 0 là
S = (– ∞; 2] ∪ [5; + ∞);
S = (– ∞; 2) ∪ (5; + ∞);
S = [2; 5];
S = (2; 5).
Trong các phát biểu sau, phát biểu nào là đúng?
Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập nghiệm của phương trình ax2 + bx + c = (dx + e)2;
Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình dx + e ≥ 0;
Mọi nghiệm của phương trình ax2 + bx + c = (dx + e)2 đều là nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\];
Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình ax2 + bx + c ≥ 0.
Trong các phát biểu sau, phát biểu nào là đúng?
Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình ax2 + bx + c = dx2 + ex + f;
Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình (ax2 + bx + c)2 = (dx2 + ex + f)2;
Mọi nghiệm của phương trình ax2 + bx + c = dx2 + ex + f đều là nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \];
Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập hợp các nghiệm của phương trình ax2 + bx + c = dx2 + ex + f thỏa mãn bất phương trình ax2 + bx + c ≥ 0 (hoặc dx2 + ex + f ≥ 0).
Số nghiệm của phương trình \(\sqrt {4 - 3{x^2}} = 2x - 1\) là
0
1
2
3
Giá trị nào sau đây là một nghiệm của phương trình\(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \)?
2;
4;
12;
20.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
\(\overrightarrow n = \left( {1;\,\, - 2} \right)\);
\(\overrightarrow n = \left( {1;\,\,2} \right)\);
\(\overrightarrow n = \left( {2;\,\, - 1} \right)\);
\(\overrightarrow n = \left( {2;\,\,1} \right)\).
Điểm nào dưới đây thuộc đường thẳng d: 3x – 2y + 4 = 0?
A(1; 2);
B(0; 2);
C(2; 0);
D(2; 1).
Phương trình tham số của đường thẳng ∆ đi qua điểm A(3; 1) và nhận \(\overrightarrow u = \left( {3;\,\, - 1} \right)\) làm vectơ chỉ phương là
\(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 - t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 + t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 + t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 - t\end{array} \right.\).
Phương trình tổng quát của đường thẳng d đi qua điểm A(2; – 2) và nhận \(\overrightarrow n = \left( {1;\,\,3} \right)\) làm vectơ pháp tuyến là
x – y + 2 = 0;
– 3x + y + 4 = 0;
x – 3y + 4 = 0;
x + 3y + 4 = 0.
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng d là
2x + y – 1 = 0;
– 2x + y – 1 = 0;
x + 2y + 1 = 0;
2x + 3y – 1 = 0.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(– 2; 3) và B(4; – 1). Phương trình nào sau đây là phương trình đường thẳng AB?
x + y – 3 = 0;
y = 2x + 2;
\(\frac{{x - 4}}{6} = \frac{{y - 1}}{{ - 4}}\);
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 - 2t\end{array} \right.\).
Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: \[\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1} = 0\\{a_2}x + {b_2}y + {c_2} = 0\end{array} \right.\] (*).
Khi đó, ∆1 song song với ∆2 khi và chỉ khi
hệ (*) có vô số nghiệm;
hệ (*) vô nghiệm;
hệ (*) có nghiệm duy nhất;
hệ (*) có hai nghiệm.
Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0. Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức
\[d\left( {M,\,\,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\];
\[d\left( {M,\,\,\Delta } \right) = \frac{{a{x_0} + b{y_0} + c}}{{\sqrt {{a^2} + {b^2}} }}\];
\[d\left( {M,\,\,\Delta } \right) = \frac{{a{x_0} + b{y_0} + c}}{{\sqrt {x_0^2 + y_0^2} }}\];
\[d\left( {M,\,\,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {x_0^2 + y_0^2} }}\].
Trong mặt phẳng tọa độ, cho hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0,
với các vectơ pháp tuyến \(\overrightarrow {{n_1}} = \left( {{a_1};\,\,b{ & _1}} \right)\) và \(\overrightarrow {{n_2}} = \left( {{a_2};\,\,b{ & _2}} \right)\) tương ứng. Khi đó góc φ giữa hai đường thẳng đó được xác định bởi công thức
\(\cos \varphi = \cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
\(\cos \varphi = - \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = - \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = - \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
\(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
\(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + a_2^2} \cdot \sqrt {b_1^2 + b_2^2} }}\).
Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là
13;
– 13;
– 1;
1.
Góc giữa hai đường thẳng a: \(\sqrt 3 \)x – y + 7 = 0 và b: x – \(\sqrt 3 \)y – 2 = 0 là
30°;
90°;
60°;
45°.
Phương trình nào sau đây là phương trình đường tròn?
2x2 + y2 – 6x – 6y – 8 = 0;
x2 + 2y2 – 4x – 8y – 12 = 0;
x2 + y2 – 2x – 8y + 18 = 0;
2x2 + 2y2 – 4x + 6y – 12 = 0.
Đường tròn (x + 1)2 + (y – 2)2 = 16 có bán kính bằng bao nhiêu?
16;
4;
256;
8.
Phương trình nào sau đây là phương trình của đường tròn tâm I(– 1; 2), có bán kính bằng 5?
(x – 1)2 + (y + 2)2 = 25;
(x + 1)2 + (y + 2)2 = 25;
(x + 1)2 + (y – 2)2 = 25;
(x – 1)2 + (y – 2)2 = 25.
Phương trình đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 là
(x – 3)2 + (y – 4)2 = 9;
(x + 3)2 + (y – 4)2 = 9;
(x – 3)2 + (y – 4)2 = 3;
(x + 3)2 + (y + 4)2 = 3.
Trong mặt phẳng tọa độ, cho đường tròn (C): (x – 2)2 + (y + 2)2 = 5. Tiếp tuyến tại điểm M(1; 0) thuộc đường tròn (C) có phương trình là
y = – 2;
x = 1;
x + 2y – 1 = 0;
x – 2y – 1 = 0.
(1 điểm) Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây:
Thời gian (s) | 0 | 0,5 | 1 | 2 | 3 |
Độ cao (m) | 0 | 28 | 48 | 64 | 48 |
Xác định hàm số bậc hai biểu thị độ cao h(m) của quả bóng gofl tính theo thời gian t(s).
Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây:
Thời gian (s) | 0 | 0,5 | 1 | 2 | 3 |
Độ cao (m) | 0 | 28 | 48 | 64 | 48 |
Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?
Cho đường thẳng d1: 2x – y – 2 = 0; d2: x + y + 3 = 0 và điểm M(3; 0). Viết phương trình đường thẳng ∆ đi qua điểm M, cắt d1 và d2 lần lượt tại A và B sao cho M là trung điểm của đoạn AB.
Cho đường tròn (C): (x – 1)2 + (y – 2)2 = 4 và đường thẳng d: x – y – 1 = 0. Viết phương trình đường tròn (C') đối xứng của (C) qua d. Tìm tọa độ giao điểm của (C), (C').