Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 5
21 câu hỏi
Từ đẳng thức \(2.15 = 6.5\) ta lập được tỉ lệ thức nào sau đây?
\(\frac{2}{{15}} = \frac{6}{5}.\)
\(\frac{2}{5} = \frac{{15}}{6}.\)
\(\frac{{15}}{2} = \frac{5}{6}.\)
\(\frac{{15}}{6} = \frac{5}{2}.\)
Nếu có dãy tỉ số bằng nhau \(\frac{a}{x} = \frac{b}{y} = \frac{c}{z}\) thì điều nào sau đây là đúng?
\(a:x = b:y = c:z.\)
\(a:z = b:y = c:x.\)
\(a:b = y:x = c:z.\)
\(a:y = b:x = c:z.\)
Cho bảng số liệu sau:

Chọn khẳng định đúng trong các khẳng định sau:
\(x\) tỉ lệ thuận với \(y\) theo hệ số \(k = 5.\)
\(x\) tỉ lệ nghịch với \(y\) theo hệ số \(a = 5.\)
\(y\) tỉ lệ thuận với \(x\) theo hệ số \(k = 5.\)
\(y\) tỉ lệ nghịch với \(x\) theo hệ số \(a = 5.\)
Biết rằng \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch với nhau. Khi \(x = - \frac{1}{2}\) và \(y = 8\) thì hệ số tỉ lệ \(a\) lúc này là
\(a = 4.\)
\(a = - 16.\)
\(a = - 4.\)
\(a = 16.\)
Trong các biểu thức sau, biểu thức đại số nào chỉ chứa một biến?
\(3x + 3y - 1.\)
\(x + 3y - z.\)
\({z^2} + 3z - 2.\)
\(3{y^2} - y - z.\)
Biểu thức đại số biểu thị tổng của hai số tự nhiên liên tiếp là
\(x + y\) với \(x,y \in \mathbb{N}.\)
\(x + y + 1\) với \(x,y \in \mathbb{N}.\)
\(x + \left( {x + 1} \right)\) với \(x \in \mathbb{N}.\)
\(x + \left( {x + 2} \right)\) với \(x \in \mathbb{N}.\)
Trong các đa thức sau, đa thức nào là đa thức một biến?
\(x + 2y.\)
\({x^2} + 2x + 1.\)
\(xy + 4x.\)
\({x^2} - 4{z^2} + y.\)
Đa thức một biến bậc \(6\) có hai hạng tử mà hệ số cao nhất là \(5\), hệ số tự do là \( - 1\). Đó là đa thức
\(6{x^5} + 1.\)
\(6{x^5} - 1.\)
\(5{x^6} + 1.\)
\(5{x^6} - 1.\)
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\widehat B = 50^\circ \). Khẳng định nào sau đây là đúng?
\(AC < AB.\)
\(BC < AB.\)
\(AC > AB.\)
\(BC < AC.\)
Cho hình vẽ sau:
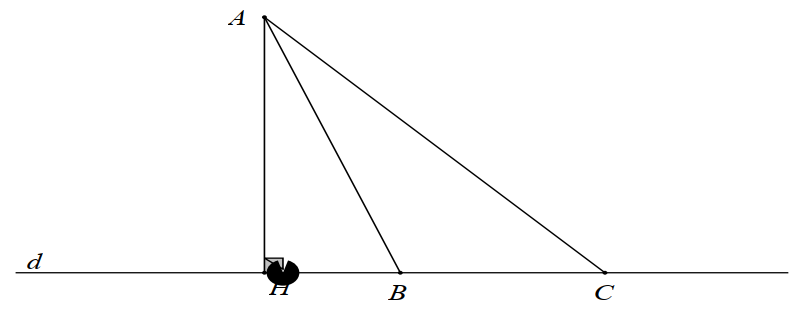
Đường vuông góc kẻ từ điểm \(A\) đến đường thẳng \(d\) là
\(AH.\)
\(AC.\)
\(AB.\)
\(BC.\)
Cho \(\Delta ABC\) có \(BC = 1{\rm{ cm, }}AC = 5{\rm{ cm}}{\rm{.}}\) Nếu \(AB\) có độ dài là một số nguyên thì \(AB\) có số đo là
\(3{\rm{ cm}}{\rm{.}}\)
\({\rm{5 cm}}{\rm{.}}\)
\({\rm{4 cm}}{\rm{.}}\)
\({\rm{6 cm}}{\rm{.}}\)
Cho \(G\) là trọng tâm của \(\Delta DEF\), vẽ đường trung tuyến \(DH.\) Trong các khẳng định sau, khẳng định nào đúng?
\(\frac{{DG}}{{DH}} = \frac{1}{2}.\)
\(\frac{{DG}}{{GH}} = 3.\)
\(\frac{{GH}}{{DH}} = \frac{1}{3}.\)
\(\frac{{GH}}{{DG}} = \frac{2}{3}.\)
Cửa hàng \(A\) bán được \(65\) chiếc bếp hồng ngoại trong một tháng gồm ba loại. Bếp hồng ngại Sunhouse giá \(10\) triệu đồng một chiếc, bếp hồng ngoại Hafele giá \(20\) triệu đồng một chiếc, bếp hồng ngoại Nagakawa giá \(12\) triệu đồng một chiếc. Biết rằng số tiền bán mỗi loại bếp hồng ngoại là như nhau. Gọi \(a,b,c\) lần lượt là số bếp hồng ngoại mà cửa hàng \(A\) bán được trong một tháng gồm bếp Sunhouse, bếp Hafele, bếp Nagakawa.
a) Điều kiện của \(a,b,c\) là \(a,b,c \in {\mathbb{N}^*}\) và \(a,b,c < 65.\)
b) Phương trình biểu diễn số bếp hồng ngoại mà cửa hàng \(A\) bán được trong một tháng là
\(abc = 65\).
c) Vì số tiền cửa hàng \(A\) bán mỗi loại bếp là như nhau nên ta có tỉ lệ thức \(\frac{a}{{10}} = \frac{b}{{20}} = \frac{c}{{12}}\).
d) Số bếp Sunhouse bán được gấp hai lần số bếp Hafele.
Cho điểm \(M\) nằm trong tam giác \(ABC\). Kẻ \(BM\) cắt cạnh \(AC\) tại \(D.\)
a) \(AB + AD \ge BD\).
b) \(MB + MD < AB + AD.\)
c) \(MB + MC < AB + AC\).
d) \(MA + MB + MC > AB + AC + BC.\)
Cho \(\frac{x}{3} = \frac{y}{6}\) và \(4x - y = 42\). Tính giá trị của \(A = 2x + 3y.\)
Trả lời:
Một hình hộp chữ nhật có các kích thước chiều dài, chiều rộng và chiều cao tỉ lệ thuận với \(5;6;7\). Biết thể tích của hình hộp là \(1680{\rm{ }}{{\rm{m}}^3}\). Hỏi chiều cao của hình hộp đó là bao nhiêu mét?
Trả lời:
Cho đa thức \(Q\left( x \right) = {x^3} - {x^2} + 2x - 3{x^2} + 5x - 2\). Tính giá trị của \(2Q\left( {\frac{1}{2}} \right) - Q\left( 1 \right)\).
(Kết quả ghi dưới dạng số thập phân)
Trả lời:
Cho một tam giác cân có số đo hai cạnh bằng \(3{\rm{ cm}}\) và \(7{\rm{ cm}}{\rm{.}}\) Hỏi chu vi tam giác cân đó bằng bao nhiêu centimet?
Trả lời:
(1,0 điểm) Một cửa hàng có ba cuộn vải với tổng chiều dài là \(186{\rm{ m}}{\rm{.}}\) Giá tiền của mỗi mét vải của ba cuộn là như nhau, sau khi bán được một ngày cửa hàng còn lại \(\frac{2}{3}\) cuộn vải loại \(I,\) \(\frac{1}{3}\) cuộn vải loại \(II\), \(\frac{3}{5}\) cuộn vải loại \(III\). Số tiền bán được của ba cửa hàng tỉ lệ với \(2:3:2\). Tính xem trong ngày đó cửa hàng đã bán được bao nhiêu mét vải của mỗi cuộn vải?
(1,0 điểm) Cho hai đoạn thẳng \(AC\) và \(BD\) cắt nhau tại trung điểm \(O\) của mỗi đoạn. Gọi \(M,N\) lần lượt là trung điểm của \(BC,CD\). Đoạn thẳng \(AM,AN\) cắt \(BD\) lần lượt tại \(I,K\). Chứng minh:
a) \(I\) là trọng tâm của \(\Delta ABC\) và \(K\) là trọng tâm của tam giác \(\Delta ADC\).
b) \(BI = IK = KD.\)
(1,0 điểm) Cho ba đa thức:
\(A\left( x \right) = 2{x^4} - 5{x^3} + 7x - 5 + 4{x^3} + 3{x^2} + 2x + 3\);
\(B\left( x \right) = 5{x^4} - 3{x^3} + 5x - 3{x^4} - 2{x^3} + 9 - 6x\);
\(C\left( x \right) = {x^4} + 4{x^2} + 5\).
a) Thực hiện tính \(A\left( x \right) + B\left( x \right)\) và \(A\left( x \right) + B\left( x \right) - 3C\left( x \right).\)
b) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.








