Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
21 câu hỏi
Các tỉ số nào sau đây có thể lập thành tỉ lệ thức?
\(3:4\) và \(5:6.\)
\(3:4\) và \(7:5.\)
\(7:5\) và \(14:10.\)
\(14:10\) và \(5:6.\)
Nếu có dãy tỉ số bằng nhau \(\frac{a}{2} = \frac{b}{3} = \frac{c}{4}\) thì điều nào sau đây là đúng?
\(x:y:z = 2:3:4.\)
\(a:b:c = 2:3:4.\)
\(a:b:c = 4:3:2.\)
\(x:y:z = 4:3:2.\)
Cho biết \(x\) và \(y\) tỉ lệ thuận với nhau có các giá trị tương ứng trong bảng sau:
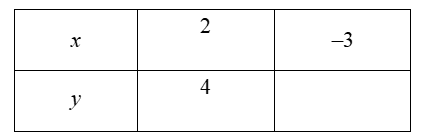
Giá trị ở ô trống trong bảng là
\( - 2.\)
\(6.\)
\( - 6.\)
\(2.\)
Cho biết \(x\) và \(y\) tỉ lệ nghịch với nhau. Khi \(x = - 6\) thì \(y = 8\). Vậy khi \(y = 12\) thì \(x\) bằng
\( - 4.\)
\(4.\)
\(16.\)
\( - 16.\)
Trong các biểu thức sau, đâu là biểu thức đại số chứa cả biến \(x\) và \(y\)?
\(x - y.\)
\({x^2} - 3x.\)
\({y^3} - 7y + 2.\)
\(x + 2{x^3} - 2z.\)
Biểu thức biểu thị quãng đường Dung đi được trong \(x\) giờ với vận tốc \(40{\rm{ km/h}}\) là
\(40.x.\)
\(40 + x.\)
\(40:x.\)
\(\frac{x}{{40}}.\)
Đa thức \(P\left( x \right) = 1 - 9{x^4} + \frac{1}{3}{x^3} + x - 1\) có hệ số tự do là
\(1.\)
\( - 1.\)
\(0.\)
\( - 2.\)
Biểu thức biểu thị “Tích của \(x\) và \(y\)” là
\(x.y.\)
\(x + y.\)
\(x - y.\)
\(\frac{x}{y}.\)
Cho \(\Delta ABC\) có \(AB = 5{\rm{ cm, }}BC = 8{\rm{ cm, }}AC = 10{\rm{ cm}}{\rm{.}}\) Khẳng định nào dưới đây là đúng?
\(\widehat B < \widehat C < \widehat A.\)
\(\widehat C < \widehat A < \widehat B.\)
\(\widehat C < \widehat B < \widehat A.\)
\(\widehat A < \widehat B < \widehat C.\)
Điền từ thích hợp điền vào chỗ trống: “Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn thì có hình chiếu…..”
lớn hơn.
ngắn nhất.
nhỏ hơn.
bằng nhau.
Bộ ba đoạn thẳng nào sau đây không thể là cạnh của một tam giác?
\(3{\rm{ cm, 4 cm, 5 cm}}{\rm{.}}\)
\({\rm{6 cm, 9 cm, 12 cm}}{\rm{.}}\)
\({\rm{2 cm, 4 cm, 6 cm}}{\rm{.}}\)
\({\rm{5 cm, 8 cm, 10 cm}}{\rm{.}}\)
Cho \(G\) là giao của hai trung tuyến \(BM\) và \(CN\) của tam giác \(ABC\) trong hình vẽ.
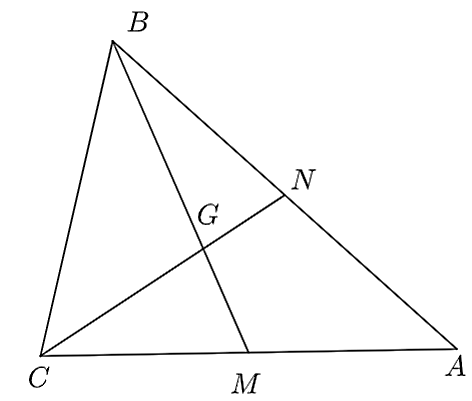
Khẳng định nào sau đây là đúng?
\(CG = \frac{{GN}}{2}.\)
\(GM = \frac{{GB}}{3}.\)
\(GB = \frac{2}{3}GC.\)
\(GN = \frac{{GC}}{2}.\)
Bác Cường mua \(39\) mớ rau gồm ba loại: rau muống giá \(6\) nghìn đồng một mớ, rau cải giá \(8\) nghìn đồng một mớ, rau đay giá \(4\) nghìn đồng một mớ. Biết rằng số tiền bác Cường mua mỗi loại rau là như nhau. Gọi \(x,y,z\) lần lượt là số mớ rau bác Cường mua gồm rau muống, rau cải và rau đay.
a) Điều kiện của \(x,y,z\) là \(x,y,z \in {\mathbb{N}^*}\) và \(x,y,z < 39.\)
b) Phương trình biểu diễn tổng số rau bác Cường mua là \(x + y + z = 39\).
c) Số tiền bác Cường mua mỗi loại rau là như nhau nên ta có tỉ lệ thức \(\frac{x}{6} = \frac{y}{8} = \frac{z}{4}.\)
d) Loại rau bác Cường mua nhiều nhất là rau đay với \(12\) mớ.
Cho tam giác \(\Delta ABC\) và \(M\) là một điểm nằm trong tam giác. Gọi \(I\) là giao điểm của đường thẳng \(BM\) và cạnh \(AC\).
a) \(MA < MI + IA.\)
b) \(MA + MB < IA + IB.\)
c) \(IA + IB < CA + CB.\)
d) \(MA + MB < CA + CB.\)
Cho \(\frac{x}{3} = \frac{y}{5}\) và \(x + y = 24\). Tính giá trị của \(3x + 5y\).
Trả lời:
Một trại chăn nuôi gồm gà, vịt và heo. Biết số con gà, vịt và heo lần lượt tỉ lệ với \(6;5;4\) và tổng số con là \(150\) con. Hỏi trại chăn nuôi có bao nhiêu con heo?
Trả lời:
Cho đa thức \(Q\left( x \right) = \frac{1}{2}{x^4} + \frac{1}{3}{x^2} - 3x + \frac{1}{2}\). Tính giá trị của \(Q\left( 3 \right) - Q\left( { - 3} \right).\)
Trả lời:
Cho tam giác \(ABC\) vuông tại \(B\) có \(AD\) là tia phân giác của \(\widehat {BAC}\) \(\left( {D \in BC} \right)\). Kẻ \(DF \bot AC\) tại \(F\). Hỏi khoảng cách từ \(D\) đến đường thẳng \(AC\) bằng bao nhiêu centimet? Biết rằng \(BD = 2{\rm{ cm}}{\rm{.}}\)
Trả lời:
(1,0 điểm) Ông Bình có một miếng đất hình chữ nhật có chiều dài hơn chiều rộng là \(20{\rm{ m}}{\rm{.}}\) Chiều dài và chiều rộng miếng đất tỉ lệ với \(9\) và \(5.\) Ông tính làm hàng rào xung quanh miếng đất bằng kẽm gai với giá \(5{\rm{ }}500\) đồng trên \(1{\rm{ m}}{\rm{.}}\) Tính chu vi mảnh vườn và số tiền ông Bình làm hàng rào biết rằng công rào và chi phí cọc là \(2{\rm{ }}500{\rm{ }}000\) đồng.
(1,0 điểm) Cho tam giác \(ABC\) có \(M\) là trung điểm của \(AC\). Trên đoạn \(BM\) lấy điểm \(K\) sao cho \(MK = \frac{1}{2}KB\). Điểm \(H\) thuộc tia đối của tia \(MK\) sao cho \(BH = 2BK.\) Gọi \(I\) là điểm thuộc cạnh \(AC\) và \(IC = \frac{1}{3}CA\). Đường \(KI\) cắt \(HC\) ở \(E\).
a) Chứng minh \(I\) là trọng tâm của \(\Delta HKC\) và \(E\) là trung điểm của \(HC.\)
b) Tính các tỉ số \(\frac{{IE}}{{IK}};\frac{{MI}}{{AC}}\).
(1,0 điểm) Cho hai đa thức:
\(F\left( x \right) = 2{x^2} - 3x + 2{x^3} - 4 + 4x - 2{x^3} - 1\) và \(G\left( x \right) = 13 - 12{x^3} + 1 - x + 12{x^3} + {x^2} + 3x\).
a) Thu gọn và sắp xếp hai đa thức trên theo chiều giảm dần lũy thừa của biến.
b) Biết rằng \(H\left( x \right) + F\left( x \right) = G\left( x \right)\). Tính \(H\left( {\frac{1}{2}} \right)\).








