Đề kiểm tra Tổng và hiệu của hai vectơ (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho các điểm phân biệt \[M,N,P,Q,R\]. Xác định vectơ tổng \[\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RP} + \overrightarrow {NP} + \overrightarrow {QR} \].
\(\overrightarrow {MP} \).
\(\overrightarrow {MN} \).
\(\overrightarrow {MQ} \).
\(\overrightarrow {MR} \).
Cho hình bình hành \(ABCD\). Trong các khẳng định sau, khẳng định nào sai?
\[\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {BC} \].
\[\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \].
\[\overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {CB} \].
\[\overrightarrow {DC} + \overrightarrow {DA} = \overrightarrow {DB} \].
Cho tam giác \(ABC\) và \(M,N,P\) lần lượt là trung điểm của \(BC,CA,AB\). Trong các khẳng định sau, khẳng định nào sai?
\(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 \).
\(\overrightarrow {AP} + \overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow 0 \).
\[\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PM} = \overrightarrow 0 \].
\[\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {MP} \].
Cho hình vuông ABCD, tâm O. Trong các khẳng định sau, khẳng định nào đúng?
\[\overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {CA} \].
\(\overrightarrow {OC} + \overrightarrow {AO} = \overrightarrow {CA} \).
\[\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CA} \].
\[\overrightarrow {DC} + \overrightarrow {BC} = \overrightarrow {CA} \].
Cho\(ABCD\)là hình bình hành tâm \(O\), \(M\) là điểm thỏa \(\overrightarrow {AM} = \overrightarrow {BC} \). Mệnh đề nào sau đây đúng?
\(M\) trùng \(D\).
\(M\) trùng \(A\).
\(M\)trùng \(B\).
\(M\) trùng \(C\).
Cho\(ABCD\)là hình bình hành tâm \(O\), \(M\) là điểm thỏa \(\overrightarrow {AM} + \overrightarrow {AB} = \overrightarrow {DC} \). Mệnh đề nào sau đây đúng?
\(M\) trùng \(O\).
\(M\) trùng \(A\).
\(M\) trùng \(B\).
\(M\) trùng \(C\).
Cho tứ giác \(PQRN\)có \(O\) là giao điểm 2 đường chéo, \(M\) là điểm thỏa \[\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} = \overrightarrow {ON} \]. Mệnh đề nào sau đây đúng?
\(M\) trùng \(P\).
\(M\) trùng \(Q\).
\(M\) trùng \(O\).
\(M\) trùng \(R\).
Cho\[\Delta ABC\], tìm điểm \(M\) thỏa \[\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {CM} - \overrightarrow {CA} \]. Mệnh đề nào sau đây đúng?
\(M\) là trung điểm \(AB\).
\(M\) là trung điểm \(BC\).
\(M\) là trung điểm \(CA\).
\(M\) là trọng tâm \[\Delta ABC\].
Cho tam giác ABC đều cạnh a, trọng tâm G. Tính độ dài vectơ \(\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right|\).
\(\frac{{2a\sqrt 3 }}{3}\)
\(\frac{a}{3}\)
\(\frac{{2a}}{3}\)
\(\frac{{a\sqrt 3 }}{3}\)
Cho hình vuông ABCD có cạnh là 3. Tính độ dài \(\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right|\):
6
\(6\sqrt 2 \)
12
0
Cho hình vuông ABCD cạnh a, tâm O và M là trung điểm AB. Tính độ dài \(\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right|\).
a
3a
\[\frac{a}{2}\]
2a
Cho \(\Delta ABC\) vuông cân tại A có \(BC = a\sqrt 2 \), M là trung điểm BC. Tính độ dài vectơ \(\left| {\overrightarrow {AB} + \overrightarrow {BM} } \right|\).
\(\frac{{a\sqrt 6 }}{2}\)
\(\frac{{a\sqrt 2 }}{2}\)
\(\frac{{a\sqrt 3 }}{2}\)
\(\frac{{a\sqrt {10} }}{2}\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Khi đó:
a) \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
b) \(\overrightarrow {AC} + \overrightarrow {BA} = \overrightarrow {AD} \)
c) \(|\overrightarrow {AB} + \overrightarrow {AD} | = AC\)
d) Nếu \(|\overrightarrow {AB} + \overrightarrow {AD} | = |\overrightarrow {CB} - \overrightarrow {CD} |\) thì \(ABCD\) là hình thoi.
Cho lục giác đều ABCDEF tâm \(O\). Khi đó:
a) \(\overrightarrow {AB} = \overrightarrow {CD} \)
b) \(\overrightarrow {AB} + \overrightarrow {OD} = \overrightarrow {AC} \)
c) \(\overrightarrow {AB} + \overrightarrow {OC} = \overrightarrow {FC} \)
d) \(\overrightarrow {AB} + \overrightarrow {AE} - \overrightarrow {FD} = \overrightarrow {AF} \)
Cho hình bình hành \(ABCD\). Hai điểm \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(AD\). Khi đó:
a) \(\overrightarrow {MC} = \overrightarrow {AN} \)
b) \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {AN} \)
c) \(\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {BM} \)
d) \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \)
Cho tam giác \(ABC\). Các điểm \(M,N,P\) lần lượt là trung điểm của \(AB,AC,BC\). Khi đó:
a) \(\overrightarrow {AM} - \overrightarrow {AN} = \overrightarrow {NM} \)
b) \(\overrightarrow {MN} - \overrightarrow {NC} = \overrightarrow {MP} \)
c) \(\overrightarrow {MN} - \overrightarrow {PN} = \overrightarrow {MP} \)
d) \(\overrightarrow {BP} - \overrightarrow {CP} = \overrightarrow {PC} \)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\). Cường độ hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \)lần lượt là 300N và 400N, \(\widehat {AMB} = 90^\circ \). Tìm cường độ của lực tác động lên vật?
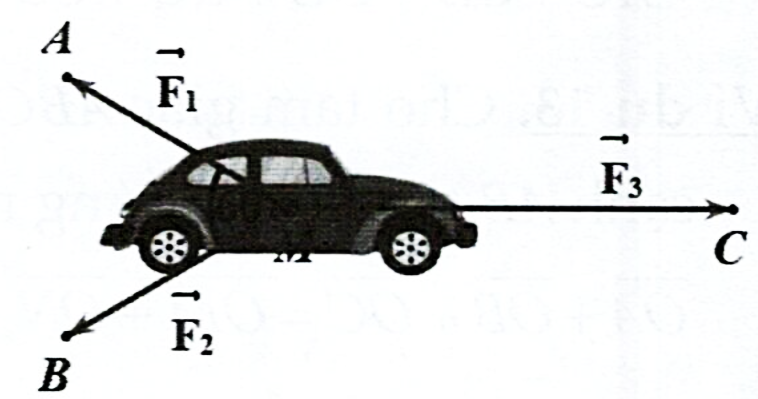
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một ô tô tại điểm \(M\) và ô tô đứng yên. Cho biết cường độ hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \)đều bằng \(25N\) và góc \(\widehat {AMB} = 60^\circ \). Khi đó tính cường độ \(\overrightarrow {{F_3}} \).
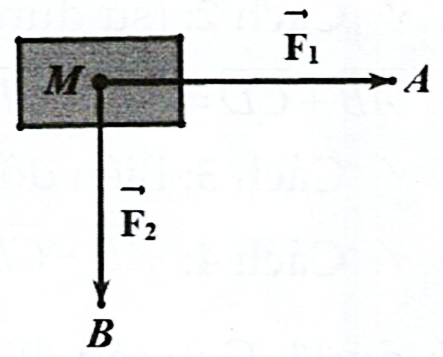
Cho hai lực \({\vec F_1},{\vec F_2}\) đều có cường độ bẳng \(100\;N\) và có cùng điểm đặt tại một điểm. Góc hợp bởi \({\vec F_1}\) và \({\vec F_2}\) bằng 900. Khi đó tính cường độ lực tổng hợp của \({\vec F_1}\) và \({\vec F_2}\)
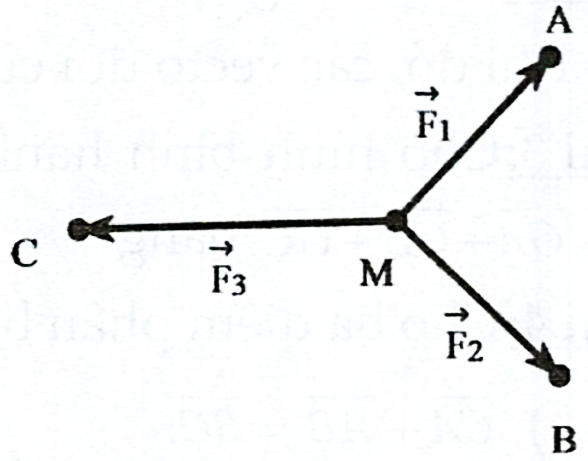
Cho ba lực \({\vec F_1} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Cho biết cường độ của \({\vec F_1},{\vec F_2}\) đều bằng \(100\;N\) và góc . Khi đó tính cường độ của lực \({\vec F_3}\).
Cho tam giác \(ABC\) vuông tại \(A\), biết \(AB = a\) và . Tính \(|\overrightarrow {AB} + \overrightarrow {BC} |\) và \(|\overrightarrow {AB} - \overrightarrow {AC} |\).
Cho hình thang ABCD có hai đáy \(AB = a,CD = 2a\). Gọi \(M,N\) lần lượt là trung điểm \(AD\) và \(BC\). Tính \(|\overrightarrow {DM} - \overrightarrow {BA} - \overrightarrow {CN} |\)








