20 câu trắc nghiệm Toán 10 Kết nối tri thức Bài 8. Tổng và hiệu của hai vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Cho ba vectơ \[\vec a\], \[\vec b\] và \[\vec c\] khác vectơ-không. Trong các khẳng định sau, khẳng định nào sai?
\[\vec a + \vec b = \vec b + \vec a\].
\[\left( {\vec a + \vec b} \right) + \vec c = \vec a + \left( {\vec b + \vec c} \right)\].
\[\vec a + \overrightarrow 0 = \vec a\].
\[\overrightarrow 0 + \vec a = \overrightarrow 0 \].
Cho hình bình hành \[ABCD\]. Vectơ tổng \[\overrightarrow {CB} + \overrightarrow {CD} \] bằng
\(\overrightarrow {CA} \).
\(\overrightarrow {BD} \).
\(\overrightarrow {AC} \).
\(\overrightarrow {DB} \).
Cho bốn điểm phân biệt \[A,B,C,D\]. Vectơ tổng \[\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \] bằng
\(\overrightarrow 0 \).
\(\overrightarrow {AC} \).
\(\overrightarrow {BD} \).
\(\overrightarrow {BA} \).
Gọi \(O\) là tâm hình bình hành \(ABCD\). Đẳng thức nào sau đây sai?
\(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {CD} .\)
\(\overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {OD} - \overrightarrow {OA} .\)
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} .\)
\(\overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {DC} - \overrightarrow {DA} .\)
Cho 4 điểm bất kỳ \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\]. Đẳng thức nào sau đây là đúng?
\[\overrightarrow {OA} = \overrightarrow {CA} + \overrightarrow {CO} \].
\[\overrightarrow {BC} - \overrightarrow {AC} + \overrightarrow {AB} = \overrightarrow 0 \].
\[\overrightarrow {BA} = \overrightarrow {OB} - \overrightarrow {OA} \].
\[\overrightarrow {OA} = \overrightarrow {OB} - \overrightarrow {BA} \].
Cho tứ giác \(ABCD\), \(M\) là điểm thỏa \(\overrightarrow {AM} = \overrightarrow {DC} + \overrightarrow {AB} + \overrightarrow {BD} \). Mệnh đề nào sau đây đúng?
\(M\) trùng \(D\).
\(M\) trùng \(A\).
\(M\) trùng \(B\).
\(M\) trùng \(C\).
Cho \[\Delta ABC\] và điểm \(M\) thỏa \[\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {CM} - \overrightarrow {CA} \]. Mệnh đề nào sau đây đúng?
\(M\) là trung điểm \(AB\).
\(M\) là trung điểm \(BC\).
\(M\) là trung điểm \(CA\).
\(M\) là trọng tâm \[\Delta ABC\].
Cho \[\Delta ABC\] và điểm \(M\) thỏa \[\overrightarrow {MC} - \overrightarrow {MB} + \overrightarrow {BM} + \overrightarrow {MA} = \overrightarrow {CM} - \overrightarrow {CB} \]. Mệnh đề nào sau đây đúng?
\(M\) trùng \(A\).
\(M\) trùng \(B\).
\(ACMB\) là hình bình hành.
\[\overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BM} \].
Cho hình thang cân ABCD, có đáy nhỏ và đường cao cùng bằng 2a và \(\widehat {ABC} = 45^\circ \). Tính \(\left| {\overrightarrow {CB} - \overrightarrow {AD} + \overrightarrow {AC} } \right|\) ta được kết quả là:
\(a\sqrt 3 \).
\(2a\sqrt 5 \).
\(a\sqrt 5 \).
\(a\sqrt 2 \).
Cho hình vuông ABCD có cạnh là a. O là giao điểm của hai đường chéo. Tính \(\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right|\) ta được kết quả là:
\(a\sqrt 3 \).
\(\frac{{a\sqrt 3 }}{2}\).
\(\frac{{a\sqrt 2 }}{2}\).
\(a\sqrt 2 \).
Phần II. Trắc nghiệm đúng, sai
Cho tam giác \(ABC\). Bên ngoài của tam giác vẽ các hình bình hành \(ABIJ,BCPQ,CARS.\)
a) \(\overrightarrow {RJ} = \overrightarrow {RA} + \overrightarrow {AJ} \).
b) \(\overrightarrow {IQ} = \overrightarrow {IB} + \overrightarrow {QB} \).
c) \(\overrightarrow {PS} = \overrightarrow {PC} + \overrightarrow {SC} \).
d) \(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 \).
Cho tam giác \(ABC\) có \(M,N\) lần lượt là trung điểm của \(AC,BC\); \(AB = a\).
a) \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN = \frac{1}{2}AB\).
b) \(\overrightarrow {NB} = \overrightarrow {CN} \).
c) \(\overrightarrow {CM} - \overrightarrow {CN} = \overrightarrow {MN} \).
d) \(\left| {\overrightarrow {CM} - \overrightarrow {NB} } \right| = \frac{a}{2}\).
Cho hình vuông \(ABCD\) có cạnh bằng \(a\).
a) \(\overrightarrow {BA} - \overrightarrow {CB} = \overrightarrow {BD} \).
b) Độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) bằng \(2a\).
c) Gọi \(E\) là điểm đối xứng với \(A\) qua \(B\). Khi đó \(\overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow {DE} \).
d) Độ dài vectơ \(\overrightarrow {DB} + \overrightarrow {DC} \) bằng \(a\sqrt 5 \).
Cho tam giác\[ABC\] với trung tuyến \[AM\] và trọng tâm \[G\].
a) \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \).
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {MC} + \overrightarrow {MB} \).
c) Vectơ \(\overrightarrow {AG} + \overrightarrow {GM} \) cùng phương với vectơ \(\overrightarrow {MG} \).
d) \(\overrightarrow {AG} + \overrightarrow {MC} = \overrightarrow {MG} + \overrightarrow {BC} \).
Cho hình thoi \(ABCD\) cạnh \(a\), có \(\widehat {BAD} = 60^\circ \). Gọi \(O\) là giao điểm hai đường chéo.
a) \(AO = \frac{{a\sqrt 3 }}{2}\).
b) \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = a\sqrt 2 \).
c) \(\left| {\overrightarrow {BA} - \overrightarrow {BC} } \right| = a\sqrt 3 \).
d) Ba lực \(\overrightarrow {{F_1}} = \overrightarrow {AB,} \,\,\overrightarrow {{F_2}} = \overrightarrow {AD,} \,\,\overrightarrow {{F_3}} \) cùng tác động vào một vật đặt tại điểm A và ở trạng thái cân bằng biết \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = 2\sqrt 3 \,{\rm{N}}\). Khi đó độ lớn của lực \(\overrightarrow {{F_3}} \) bằng \(6\,{\rm{N}}\).
Phần III. Trắc nghiệm trả lời ngắn
Có hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) cùng tác động vào một vật đứng tại điểm \(O\), biết hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều có cường độ là \(50\,\,\left( {\rm{N}} \right)\) và chúng hợp với nhau một góc \(60^\circ \). Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu Newton (làm tròn kết quả đến hàng phần mười)?
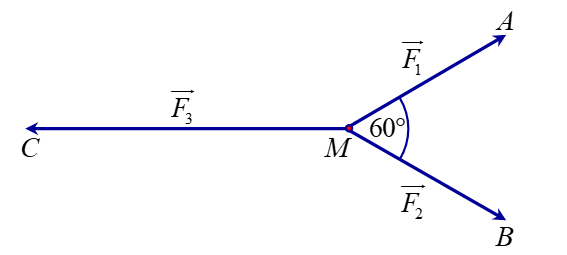
Cho ba lực \[\overrightarrow {{F_1}} = \overrightarrow {MA} \], \[\overrightarrow {{F_2}} = \overrightarrow {MB} \], \[\overrightarrow {{F_3}} = \overrightarrow {MC} \] cùng tác động vào một vật tại điểm \[M\] và vật đứng yên. Cho biết cường độ của \[\overrightarrow {{F_1}} \], \[\overrightarrow {{F_2}} \] đều bằng \[25\,{\rm{N}}\] và \[\widehat {AMB} = 60^\circ \]. Khi đó cường độ lực của \[\overrightarrow {F_3^{}} \]bằng \(a\sqrt 3 \) N. Xác định giá trị của \(a\).
Cho tam giác \(ABC\,\,\left( {AB < AC} \right),AD\) là phân giác trong của góc \(A\). Qua trung điểm \(M\) của cạnh \(BC\), ta kẻ đường thẳng song song với \(AD\), cắt cạnh \(AC\) tại \(E\) và cắt tia \(BA\) tại \(F\). Biết rằng \(AB = 6\) và \(4BD = 3BM\). Tính \(\left| {\overrightarrow {CM} - \overrightarrow {EM} } \right|\).
Một dòng sông chảy từ phía Bắc xuống phía Nam với vận tốc \(10{\rm{\;km/h}}\), có một chiếc ca nô chuyển động từ phía Đông sang phía Tây với vận tốc \(35\;{\rm{km/h}}\) so với dòng nước. Tìm vận tốc của ca nô so với bờ (đơn vị: km/h, làm tròn kết quả đến hàng phần mười)?
Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\). Cường độ hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là 400 N và 300 N, \(\widehat {AMB} = 90^\circ \). Cường độ của lực tác động lên vật bằng bao nhiêu Newton?