Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 2

Nguyên hàm của hàm số $y=f\left(x\right)=\sin \left(\frac{\pi }{2}-x\right)$ là:

Nếu $\underset{2}{\overset{3}{\int }}f\left(x\right)dx=5$ thì giá trị của $I=\underset{2}{\overset{3}{\int }}2f\left(x\right)dx$ bằng

Cho hàm số f (x) biết $\underset{0}{\overset{9}{\int }}f\left(x\right)dx=9$. Tích phân $\underset{0}{\overset{3}{\int }}f\left(3x\right)dx$ bằng

Cho số phức z = 1 + 2i. Môđun số phức $\frac{z}{\overline{z}}+\frac{\overline{z}}{z}$ bằng

Cho z = 1 + 2i; w = 8 - 6i. Tính $\omega =\frac{z}{w}$

$\int \sin xdx$ bằng

Trong không gian Oxyz, phương trình mặt phẳng qua điểm M(3; -1; 1) có véc tơ pháp tuyến $\overrightarrow{a}=\left(-1;3;-2\right)$ là

Biết $\underset{1}{\overset{3}{\int }}f\left(x\right)dx=3;\underset{5}{\overset{1}{\int }}f\left(x\right)dx=-1$. Giá trị của $I=\underset{3}{\overset{5}{\int }}f\left(x\right)dx$ là

Số phức z = 3a + 4bi với a; b là các số thực khác 0. Số phức z^-1 có phần ảo là

Cho z₁ = 2 + 3i; z₂ = -1 + 5i. Số phức z₁ - z₂ là

Trong không gian Oxyz, phương trình mặt phẳng đi qua điểm M(1; -1; 0) và vuông góc với đường thẳng $\left(d\right):\frac{x}{1}=\frac{y+2}{2}=\frac{z-1}{-2}$ là

Cho số phức z thỏa mãn $iz={\left(2\sqrt{3}+i\right)}^2\left(1-\sqrt{2}i\right)$ . Phần thực của z là

Biết F(x) là một nguyên hàm xủa hàm số f (x) = e^x + 2x thỏa mãn F (1) = e. Khi đó, F (x) bằng

Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm P(1; -1; 2); Q(2; 0; 1) là

Trong hệ tọa độ Oxyz cho M(2; 5; -1) và N(4; 3; 0) độ dài đoạn thẳng MN bằng

Nguyên hàm của hàm số $f\left(x\right)=\frac{1}{2x}$ trên (0; +¥), biết $F\left(e\right)=\frac{e}{2}$ là

Cho hai số phức z = 3 + 2i; w = 1 - i. Mô đun của số phức $\overline{z}.w$ bằng:

Số phức liên hợp của số phức z = 5 - 7i là

Số phức -6 + 3i có phần thực bằng

Tọa độ tâm mặt cầu (S) đi qua các điểm O(0; 0; 0); A(3; 0; 0); B(3; 0; 3); C(3; 3; 3) là

Cho hàm số y = f (x) liên tục trên ℝ có đồ thị như hình bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số f (x), x = 0; x = c, trục hoành. Khẳng định nào sau đây đúng?

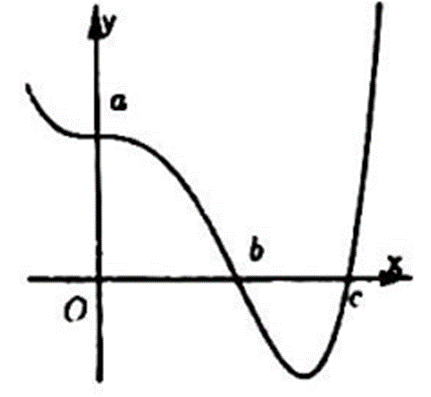
Tìm khẳng định SAI trong các khẳng định sau?

Họ tất cả các nguyên hàm F (x) của hàm số $f\left(x\right)=x-\frac{1}{x}$ với x Î (-¥; 0) là

Cho số phức z = 2 - 2i. Mô đun của số phức $\frac{z}{1+i}$ bằng

Nguyên hàm của hàm số y = 3^x là:

Trong không gian Oxyz, mặt cầu (S): x² + (y - 4)² + (z + 1)² = 25 có tâm là điểm

Diện tích hình phẳng giới hạn bởi các đường $y=\frac{2x-1}{x-1};y=0;x=0;x=-1$ bằng

Hàm số f (x) liên tục trên ℝ và có đồ thị như hình bên. Khẳng định nào sau đây là SAI.

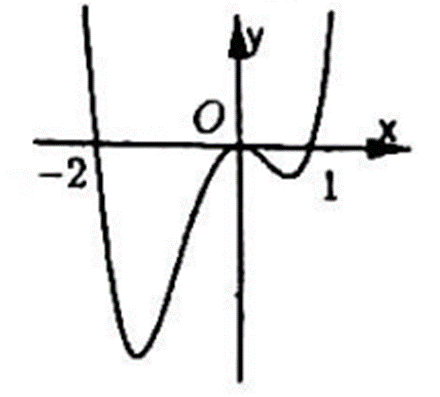
Nguyên hàm của hàm số f (x) = 3x² là

Cho $\underset{0}{\overset{2}{\int }}f\left(x\right)dx=-2$và $\underset{0}{\overset{2}{\int }}g\left(x\right)dx=3$. Ta có $I=\underset{0}{\overset{2}{\int }}\left[x+2f\left(x\right)-3g\left(x\right)\right]dx$ bằng

Diện tích S hình phẳng giới hạn bởi các đường thẳng y = x³ + 1; y = 0; x = 0; x = 1 là

Trong mặt phẳng tọa độ, biết điểm M(3; -4) là điểm biểu diễn số phức z. Mô đun của z bằng

Trong không gian Oxyz, cho $\overrightarrow{a}=\left(3;-4;1\right);\overrightarrow{b}=\left(2;1;5\right)$; véc tơ $\overrightarrow{u}=2\overrightarrow{a}-3\overrightarrow{b}$ có tọa độ

Phương trình mặt phẳng đi qua điểm A(1; 2; -1) và vuông góc với hai mặt phẳng có phương trình 2x + y = 0 và x = z + 1

Trong hệ tọa độ Oxyz điểm M' đối xứng của điểm N(2; 3; -4) qua gốc tọa độ O có tọa độ

Hàm số f (x) có đạo hàm liên tục trên đoạn [a; b] và f (a) = -5; f (b) = 1. Tích phân $I=\underset{a}{\overset{b}{\int }}{f}^{\text{'}}\left(x\right)dx$ bằng

Gọi z₁; z₂ là hai nghiệm của phương trình 2z² - 5z + 10 = 0. Giá trị của z₁² + z₂² bằng

Biết F (x) là một nguyên hàm của hàm số f (x); "x Î (-¥; +¥). Hàm số nào sau đây là một nguyên hàm của hàm số f (x + 2)?

Tọa độ hình chiếu vuông góc của điểm M(1; -1; 2) trên mặt phẳng (P): 2x - y + 2z + 12 = 0 là

Trong không gian Oxyz, giao tuyến của hai mặt phẳng x + 2y + z - 1 = 0, 2x - y - z + 4 = 0 là đường thẳng có phương trình là

Cho (d): x = y = z; (P): x + z - 1 = 0; (Q): y + 1 = 0. Gọi (D) là đường thẳng giao tuyến của (P) và (Q). Khoảng cách giữa hai đường thẳng (d) và (D) là

Phương trình z³ = 1 có ba nghiệm phức phân biệt và A; B; C là các điểm biểu diễn ba số phức đó trên mặt phẳng phức. Trọng tâm tam giác ABC có tọa độ là

Cho số phức z. Biểu thức |z + 1|² + |z - 1|² - 2 có giá trị bằng giá trị của biểu thức nào sau đây

Cho hàm số $y=f\left(x\right)=\left\{\begin{array}{c}2x+3\left(x\ge -1\right)\\ 3x^2-2\left(x\le -1\right)\end{array}\right..$ Gọi F (x) là nguyên hàm của hàm số f (x) trên ℝ thỏa mãn F (0) = 2; F (-2) = 1. Giá trị của F (1) - F (-3) bằng

Hàm số y = f (x) có đạo hàm liên tục trên ℝ thỏa mãn f (1) = 1; f (2) = 4. Tích phân $J=\underset{1}{\overset{2}{\int }}\left[\frac{f^{\text{'}}\left(x\right)+2}{x}-\frac{f\left(x\right)+1}{x^2}\right]dx$ bằng

Trong không gian Oxyz, phương trình mặt phẳng chứa đường thẳng (d): x - 1 = y - 2 = z + 1 và có khoảng cách đến điểm A(2; 3; -3) lớn nhất có phương trình

Cho (H) là hình phẳng giới hạn bởi các đường $y=\sqrt{x}$ và y = x². Thể tích khối tròn xoay tạo thành khi quay hình (H) quay quanh trục Ox bằng

Biết z₁; z₂ = 4 + 2i là hai nghiệm của phương trình ax² + bx + c = 0; (a; b; c Î ℝ và a ¹ 0), Giá trị của T = |z₁| + 3|z₂| là

Họ nguyên hàm của hàm số $f\left(x\right)=\frac{1}{x^2-2x}$ trên khoảng (2; +¥) là