Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 1

Trên tập số phức, cho số phức z có biểu diễn hình học là điểm M ở hình vẽ sau.

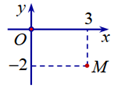
Khẳng định nào sau đây đúng?

Biết $\underset{1}{\overset{2}{\int }}x\ln \text{xdx}$= aln2 + $\frac{b}{4}$ trong đó a, b là các số nguyên. Tính a + b.

Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = $\frac{1}{\cos \text{x}}$, trục hoành và các đường thẳng x = 0, x = $\frac{\pi }{4}$. Khối tròn xoay tạo thành khi quay (H) quanh trục hoành có thể tích bằng

Cho số phức z thỏa mãn 2z + 3 = 15 − 4i. Phần ảo của z bằng

Cho hai số phức z = 4 + 3i và w = 2 + i. Số phức iz + $\overline{\text{w}}$ bằng

Trong không gian Oxyz, cho hai điểm M (2; 1; 0) và N (4; 3; 2). Gọi (P) là mặt phẳng trung trực của MN, phương trình của mặt phẳng (P) là

Họ tất cả các nguyên hàm của hàm số f (x) = $\frac{1}{2\text{x}-4}$ là

Cho hai số phức z = 4 + 3i và w = 2 + i. Số phức z + w bằng

Hàm số F (x) = x + $\frac{1}{x}$ (với x ≠ 0) là một nguyên hàm của hàm số nào sau đây?

Hàm số nào sau đây là một nguyên hàm của hàm số f (x) = xcosx?

y = x³ + 3x (C). Gọi (d) là tiếp tuyến của (C) tại điểm M (1; 4). Tính diện tích hình phẳng giới hạn bởi (C), (d) và trục hoành

Trong không gian Oxyz, đường thẳng đi qua hai điểm A (1; 0; 2) và B (4; 1; 0) có phương trình tham số là

Có bao nhiêu số phức thỏa mãn |z| (z − 3 − i) + 2i = (4 − i)z?

Cho hàm số f (x) thỏa mãn f(x) = 5^x và f (0) = $\frac{2}{\ln 5}$ . Mệnh đề nào dưới đây đúng?

Cho số phức z thỏa mãn $\frac{z}{4+3i}$ = 2. Môđun của số phức z bằng

Trong không gian Oxyz, mặt phẳng nào sau đây đi qua gốc tọa độ và vuông góc với đường thẳng $\frac{x-1}{-2}$ = $\frac{y+2}{-1}$ = $\frac{z-3}{2}?$

Trong không gian Oxyz, mặt cầu (S): x² + y² + z² − 4x + 2y + 6z − 11 = 0 có bán kính bằng

Tìm họ nguyên hàm của hàm số f (x) = $\frac{1}{co{s}^2\text{x}}$ − $\frac{1}{\mathrm{s}{\text{in}}^2\text{x}}$.

Trong không gian Oxyz, cho hai điểm A (1; 2; 2) và B (3; 1; 0). Độ dài đoạn AB bằng

Trong không gian Oxyz, cho đường thẳng d: $\frac{x-2}{2}$= $\frac{y+3}{-1}$= $\frac{z-1}{3}$. Mặt phẳng (P) vuông góc với đường thẳng d, có vectơ pháp tuyến là

Biết F(x) = x² + x − 1 là một nguyên hàm của hàm số f (x) trên ℝ. Tính $\underset{0}{\overset{3}{\int }}\left[4+f\left(x\right)\right]d\text{x}$

Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overrightarrow{a}$ = (1; 2; 3) và  $\overrightarrow{b}$= (3; 2; 1). Tính $\overrightarrow{a}$.$\overrightarrow{b}$.

Tính tổng phần thực và phần ảo của số phức z = 1 + 2i.

Tìm $\int 2^x{.3}^{x}d\text{x}$

Trong không gian Oxyz, cho hai điểm A (1; 2; 2) và B (3; 1; 0). Tọa độ của vectơ $\overrightarrow{AB}$ là

Trong không gian Oxyz, cho tứ diện ABCD với A(3; −1; 1), B(−1; 0; 0), C(0; 1; 0), D(0; 0; 2). Chiều cao AH của tứ diện ABCD bằng:

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1; −2; 3) và cắt mặt phẳng Oxy tạo ra đường tròn giao tuyến có chu vi bằng 8π. Phương trình của mặt cầu (S) là

Trong hệ trục tọa độ Oxyz cho điểm hai điểm A(1; 2; 3), B(0; 1; −6) và mp (P): 4x − y + 2z + 13 = 0. Gọi (d) là một đường thẳng thuộc (P), (d) đi qua B. Khi khoảng cách từ A đến (d) đạt giá trị nhỏ nhất. Tìm vectơ chỉ phương của đường thẳng (d)

Cho số phức z thỏa mãn ($\overline{z}$+ 2i). (z − 4) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức w = (1 + i). z + 1 − 2i là đường tròn có bán kính bằng:

Trong không gian Oxyz, cho mặt phẳng (P) đi qua I(2; –3; 1) cắt các trục Ox, Oy, Oz lần lượt tại A(2; 0; 0), B(0; b; 0), C(0; 0; c) với b > 0, c > 0 sao cho thể tích khối tứ diện OABC bằng 1. Giá trị của b + c bằng

Cho hàm số y = f (x) liên tục trên R và thỏa mãn $\underset{1}{\overset{4}{\int }}\frac{f\left(\sqrt{x}\right)}{\left(\sqrt{x}+1\right)}d\text{x}$= 4, $\underset{1}{\overset{2}{\int }}\ln \left(x+1\right)f\text{'}\left(x\right)d\text{x}$ = 1 + 3ln3, f (1) = 0, f (2) = 3. Tính E = $\underset{1}{\overset{2}{\int }}f\left(x\right)d\text{x}$.