Đề kiểm tra Hệ trục tọa độ trong không gian (có lời giải) - Đề 5
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 10. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Trong không gian \(Oxyz\), cho điểm \[M\] thỏa mãn hệ thức \[\overrightarrow {OM} = \overrightarrow i - 5\overrightarrow j + 2\overrightarrow k \]. Tọa độ điểm \[M\] là
\(M\left( {1;5;2} \right)\).
\(M\left( {2;5;1} \right)\).
\(M\left( {2; - 5;1} \right)\).
\(M\left( {1; - 5;2} \right)\).
Trong không gian \(Oxyz\), cho \[A\left( {1; - 1;3} \right)\] và \[B\left( {1;3; - 2} \right)\]. Tọa độ của vectơ \[\overrightarrow {AB} \] là
\[\overrightarrow {AB} = \left( {0;4; - 5} \right)\].
\[\overrightarrow {AB} = \left( {0; - 4;5} \right)\].
\[\overrightarrow {AB} = \left( {2;2;1} \right)\].
\[\overrightarrow {AB} = \left( {2;4;5} \right)\].
Trong không gian \(Oxyz\), cho \[\overrightarrow u = \left( {1;0;2} \right)\] và \[\overrightarrow v = \left( {3;2; - 1} \right)\]. Tọa độ của vectơ \[\overrightarrow u + \overrightarrow v \] là
\[\left( {1;2;4} \right)\].
\[\left( { - 2; - 2;3} \right)\].
\[\left( {4;2;1} \right)\].
\[\left( {2;2; - 3} \right)\].
Trong không gian \(Oxyz\), cho \[\overrightarrow u = \left( {5; - 1;2} \right)\] và \[\overrightarrow v = \left( { - 1;2;1} \right)\]. Tọa độ của vectơ \[\overrightarrow u - \overrightarrow v \] là
\[\left( {4; - 1;1} \right)\].
\[\left( {6; - 3;1} \right)\].
\[\left( { - 6;3; - 1} \right)\].
\[\left( { - 4;1; - 1} \right)\].
Trong không gian \[Oxyz\] cho tam giác \[ABC\] có \[A\left( {1; - 1;1} \right),\,B\left( {5;0;2} \right),\,C\left( {0;4;3} \right)\]. Toạ độ trọng tâm \(G\)của tam giác \[ABC\] là
\(G\left( {3;\frac{5}{2};3} \right)\).
\(G\left( {2; - 1;2} \right)\).
\(G\left( {3; - \frac{5}{2};3} \right)\).
\(G\left( {2;1;2} \right)\).
Trong không gian \(Oxyz\), cho vectơ \(\vec a = \left( {2\,; - 1\,;5} \right)\). Tọa độ vectơ \( - 5\vec a\) là
\[\left( { - 10;5; - 25} \right)\]
\[\left( {10; - 5;25} \right)\]
\[\left( {7;4;10} \right)\]
\[\left( { - 3;6;0} \right)\]
Trong không gian \(Oxyz\), khoảng cách giữa \(2\)điểm \[M\left( {1; - 3;7} \right)\] và \[N\left( {2;3; - 1} \right)\]là
\(101\).
\(10\).
\(\sqrt {101} \).
\(11\).
Trong không gian \(Oxyz\), cho \[\overrightarrow u = \left( {1; - 1;4} \right)\] và \[\overrightarrow v = \left( {3; - 2;1} \right)\]. Khi đó \[\overrightarrow u .\overrightarrow v \] bằng
\[ - 9\].
\[9\].
\[7\].
\[ - 3\].
Trong không gian \(Oxyz\), cho \[\overrightarrow u = \left( {2; - 1;0} \right)\] và \[\overrightarrow v = \left( { - 1; - 2;7} \right)\]. Góc hợp bởi \(2\) vectơ đã cho bằng
\[30^\circ \].
\[90^\circ \].
\[60^\circ \].
\[45^\circ \].
Trong không gian \(Oxyz\), cho \[\overrightarrow u = \left( {1; - 1;5} \right)\] và \[\overrightarrow v = \left( {2; - 4;7} \right)\]. Tính \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) ?
\[\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( { - 13; - 3;2} \right)\].
\[\left[ {\overrightarrow u ,\overrightarrow v } \right] = 41\].
\[\left[ {\overrightarrow u ,\overrightarrow v } \right] = - 41\].
\[\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {13;3; - 2} \right)\].
Trong không gian với hệ tọa độ \(Oxyz\), cho véc-tơ \(\overrightarrow {AO} = 3\left( {\overrightarrow i + 4\overrightarrow j } \right) - 2\overrightarrow k + 5\overrightarrow j \). Tọa độ của điểm \(A\) là
\(\left( {3\,;\,17\,;\, - 2} \right)\).
\(\left( { - 3\,;\, - 17\,;\,2} \right)\).
\(\left( {3\,;\, - 2\,;\,5} \right)\).
\(\left( {3\,;\,5\,;\, - 2} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], tọa độ điểm đối xứng của \(M\left( {1;2;3} \right)\) qua mặt phẳng \(\left( {Oyz} \right)\) là
\(\left( {0;2;3} \right)\).
\(\left( { - 1; - 2; - 3} \right)\).
\(\left( { - 1;2;3} \right)\).
\(\left( {1;2; - 3} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 11 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Trong không gian \(Oxyz\), cho các vectơ \(\overrightarrow u = 3\overrightarrow i + \overrightarrow j \, - 2\overrightarrow k ,\,\,\,\overrightarrow v = 2\overrightarrow i - \overrightarrow k ,\,\,\,\overrightarrow m = 2\overrightarrow u - 3\overrightarrow v \,\).
Mệnh đề | Đúng | Sai |
a) \(\overrightarrow u = \left( {3;1; - 2} \right)\). |
|
|
b) \(\overrightarrow v = \left( {2; - 1;0} \right)\). |
|
|
c) \(2\overrightarrow u = \left( {6;1; - 2} \right)\). |
|
|
d) \(\overrightarrow m = \left( {0;2; - 1} \right)\). |
|
|
Trong không gian \(Oxyz\), cho các điểm \(A\left( {1; - 2;3} \right),\,\,B\left( { - 2;1;2} \right),\,\,C\left( {3; - 1;2} \right)\). Xét tính đúng sai của các phát biểu sau:
Mệnh đề | Đúng | Sai |
a) \(\overrightarrow {AB} = \left( { - 3;3 - 1} \right)\). |
|
|
b) \(\overrightarrow {AC} = \left( { - 2; - 1;1} \right)\). |
|
|
c) \(\overrightarrow {AB} = 3\overrightarrow {AC} \). |
|
|
d) Ba điểm \(A,\,B,\,C\)không thẳng hàng. |
|
|
Trong không gian \(Oxyz\), cho hình bình hành \(ABCD\) có \(A\left( {2; - 1; - 2} \right),\,\,B\left( {3;1;2} \right),\,\,C\left( {1; - 1;1} \right)\) và \(D\left( {{x_D};{y_D};{z_D}} \right)\). Xét tính đúng sai của các phát biểu sau:
Mệnh đề | Đúng | Sai |
a) \(\overrightarrow {AB} = \left( {1;2;4} \right)\). |
|
|
b) \(\overrightarrow {DC} = \left( {1 - {x_D}; - 1 - {y_D};1 - {z_D}} \right)\). |
|
|
c) \(\overrightarrow {DC} = \overrightarrow {AB} \). |
|
|
d) \({x_D} + {y_D} + {z_D} = 2\) |
|
|
Trong không gian \[Oxyz,\]cho hình hộp \[ABCD.A'B'C'D'\] có \[A\left( {1;0;1} \right),B\left( {2;1;2} \right),D\left( {1; - 1;1} \right)\], \[A'\left( {1;1; - 1} \right)\] và \[B'\left( {{b_1};{b_2};{b_3}} \right)\]. Xét tính đúng sai của các phát biểu sau:
Mệnh đề | Đúng | Sai |
a) \(\overrightarrow {A'A} = \left( {0; - 1;2} \right)\). |
|
|
b) \(\overrightarrow {B'B} = \left( {2 - {b_1};1 - {b_2};2 - {b_3}} \right)\). |
|
|
c) \(\overrightarrow {A'A} = \overrightarrow {B'B} \). |
|
|
d) \[B'\left( {2;0;\,0} \right)\] |
|
|
PHẦN III. CÂU HỎI TRẢ LỜI NGẮN
Trong không gian \(Oxyz\), cho hình bình hành \(ABCD\). Biết \(A\left( {1;3;2} \right)\),\(B\left( {2;0; - 2} \right)\),\(D\left( { - 3;7;1} \right)\), và\(C\left( {a\,;\,b\,;\,c} \right)\). Tìm \(a + 3b + 4c\).
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \[M\left( {2;3; - 4} \right)\] trên mặt phẳng \[\left( {Oyz} \right)\] là điểm \(H\left( {m\,;\,n\,;\,p} \right)\). Tìm \(T = m - 2n - 3p\).
Trong không gian tọa độ \(Oxyz\), hình chiếu của điểm \(M\left( {3\,;\, - 7\,;4} \right)\) trên trục \(Oy\) là điểm \(H\left( {a\,;\,b\,;\,c} \right)\). Khi đó giá trị của \(a - b + c\) bằng bao nhiêu?
Ở một sân bay, ví trí của máy bay được xác định bởi điểm \(M\) trong không gian \(Oxyz\) (như hình vẽ ).
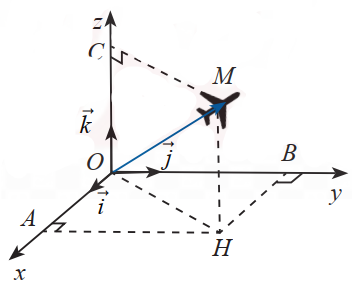
Gọi \(H\) là hình chiếu vuông góc của \(M\left( {a\,;\,b\,;\,c} \right)\) xuống mặt phẳng \(\left( {Oxy} \right)\). Cho biết \(OM = 50,\)\(\left( {\vec i\,,\,\overrightarrow {OH} } \right) = 64^\circ \,,\,\,\,\left( {\overrightarrow {OH\,} \,,\,\,\overrightarrow {OM\,} } \right) = 48^\circ \). Tìm \(S = a + b + c\)(kết quả làm tròn đến 1 chữ số sau dấu phẩy).
Tìm toạ độ của các vectơ ở Hình 30.
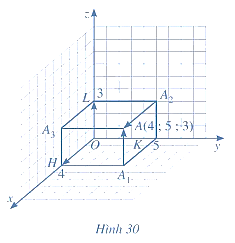
Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ \(Oxyz\) được thiết lập như hình bên dưới, cho biết \(M\) là vị trí của máy bay, \(OM = 14,\,\,\widehat {NOB} = 32^\circ ,\,\,\widehat {MOC} = 65^\circ \). Tìm tọa độ điểm \(M\).