Đề kiểm tra Hệ trục tọa độ trong không gian (có lời giải) - Đề 4
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 10. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(M\left( {1;2;3} \right)\). \({M_1}\)là hình chiếu của \(M\) lên trục \[Ox\,,\]\({M_1}\)có tọa độ là:
\({M_1}\left( {0;0;3} \right)\).
\({M_1}\left( {0;2;0} \right)\).
\({M_1}\left( {1;0;0} \right)\).
\({M_1}\left( {0;2;3} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(M\left( {1; - 2; - 3} \right)\). \({M_1}\)là hình chiếu của \(M\) trên mặt phẳng tọa độ \[Oxy\], \({M_1}\)có tọa độ là:
\({M_1}\left( {0; - 2; - 3} \right)\).
\({M_1}\left( { - 1;2;3} \right)\).
\({M_1}\left( {1; - 2;0} \right)\).
\({M_1}\left( {0;2;3} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), có \({M_1}\left( { - 1;0;0} \right),{M_2}\left( {0;2;0} \right),{M_3}\left( {0;0; - 3} \right)\)lần lượt là hình chiếu của \(M\) trên các trục \[Ox\,,\,Oy\,,\,Oz\], tọa độ điểm \(M\) là:
\({M_1}\left( {1; - 2;3} \right)\).
\({M_1}\left( { - 1;2;3} \right)\).
\({M_1}\left( { - 1;2; - 3} \right)\).
\({M_1}\left( { - 1; - 2;3} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(A\left( {2; - 2;3} \right)\). Biểu diễn \(\overrightarrow {OA} \) theo các véc tơ \(\overrightarrow i \,,\,\overrightarrow j \,,\overrightarrow k \).
\(\overrightarrow {OA} = 2\overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \).
\(\overrightarrow {OA} = 2\overrightarrow i + 2\overrightarrow j + 3\overrightarrow k \).
\(\overrightarrow {OA} = - 2\overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \).
\(\overrightarrow {OA} = - 2\overrightarrow i + 2\overrightarrow j + 3\overrightarrow k \).
Trong không gian với hệ tọa độ \(Oxyz\), cho \(\overrightarrow u = \left( {1;0; - 2} \right)\). Xác định tọa độ điểm \(A\) biết \(\overrightarrow {OA} = \overrightarrow u \).
\(A(1\,;\,0\,;\,2)\).
\(A(1\,;\,0\,;\,\, - 2)\).
\(A( - 1\,;\,0\,;\,2)\).
\(A( - 1\,;\,0\,;\, - 2)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho \(\overrightarrow u = 2\overrightarrow j - \overrightarrow i + \overrightarrow k \) . Tọa độ véc tơ \(\overrightarrow u \) là: \(\)
\(\overrightarrow u (2\,;\, - 1\,;\,1)\).
\(\overrightarrow u ( - 1\,;\,2\,;\,1)\).
\(\overrightarrow u (2\,;\, - 1\,;\, - 1)\).
\(\overrightarrow u ( - 1\,;\,1\,;\,2)\).
Cho \(A\left( {1;\,\,1;\, - 2} \right)\) và \(B\left( {2;\,\, - 1;\,\,0} \right)\). Hãy xác định tọa độ của \(\overrightarrow {AB} \)?
\(\overrightarrow {AB} = \left( { - 1;\,\,2;\,\, - 2} \right)\).
\(\overrightarrow {AB} = \left( {1;\,\,2;\,\,2} \right)\).
\(\overrightarrow {AB} = \left( {3;\,\,0;\,\, - 2} \right)\).
\(\overrightarrow {AB} = \left( {1;\, - \,2;\,\,2} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;\, - 1;\,1} \right)\), \(B\left( {3;2; - 2} \right)\), \(C\left( { - 3;1;5} \right)\). Tìm tọa độ điểm \(D\) thỏa mãn \(\overrightarrow {AB} = \overrightarrow {CD} \).
\(D\left( { - 1;\,4;\,2} \right)\).
\(D\left( {1; - \,4; - \,2} \right)\).
\(D\left( {1;\,4;\,2} \right)\).
\(D\left( { - 1; - \,4;\,2} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], với \[\overrightarrow i ,\overrightarrow j ,\overrightarrow k \] lần lượt là các vecto đơn vị trên các trục \[Ox,\,\,Oy,\,\,Oz.\] Tính tọa độ của vecto \[\overrightarrow i + \overrightarrow j - \overrightarrow k .\]
\[\left( { - 1; - 1;1} \right)\].
\[\left( { - 1;1;1} \right)\].
\[\left( {1;1; - 1} \right)\].
\[\left( {1; - 1;1} \right)\].
Trong không gian với hệ toạ độ \(Oxyz\), cho 3 điểm \(M\left( {2\,;\,0\,;\,0} \right)\); \(N\left( {0\,;\, - 3\,;\,0} \right)\); \(P\left( {0\,;\,0\,;\,4} \right)\). Nếu \(MNPQ\) là hình bình hành thì toạ độ của điểm \(Q\) là
\(\left( { - 2\,;\, - 3\,;\,4} \right)\).
\(\left( {3\,;\,4\,;\,2} \right)\).
\(\left( {2\,;\,3\,;\,4} \right)\).
\(\left( { - 2\,;\, - 3\,;\, - 4} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình chữ nhật \(OKMN\) ( hình vẽ bên).
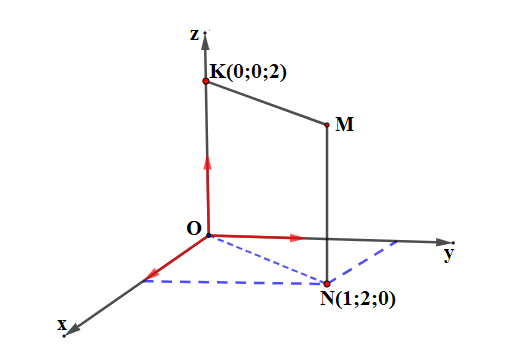
Tọa độ đỉnh \(M\)của hình chữ nhật là:
\(M\left( {1;\,2;\,2} \right)\).
\(M\left( { - 1; - \,2;\, - 2} \right)\).
\(M\left( {0;\,2;\,2} \right)\).
\(M\left( {1;2;\,0} \right)\).
Trong không gian với hệ trục tọa độ \[Oxyz\], cho ba điểm \[A(1;2; - 1)\], \[B(2; - 1;3)\],\[C( - 2;3;3)\]. Điểm\[D\left( {a;\,b;\,c} \right)\] là đỉnh thứ tư của hình bình hành \[ABCD\], khi đó \(P = {a^2} + {b^2} - {c^2}\) có giá trị bằng
\[42\].
\[43\].
\[44\].
\[45\].
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 11 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho tứ diện \(ABCD\). Gọi \(M,N,G\) lần lượt là trung điểm của \(AB\), \(CD\), \(MN\).
a) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \).
b) \(\overrightarrow {MC} + \overrightarrow {MD} = 2\overrightarrow {MN} \).
c) \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} + \overrightarrow {GD} \).
d) \(\overrightarrow {AD} + \overrightarrow {BC} = \overrightarrow {MN} \).
Cho lập phương \(ABCD.A'B'C'D'\)có cạnh bằng \(a.\)
a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
b) \(\left( {\overrightarrow {AC} ,\overrightarrow {D'A'} } \right) = {45^0}\).
c) \(\overrightarrow {BD} .\overrightarrow {A'C'} = 0\).
d) \(\overrightarrow {AC'} .\overrightarrow {AB} = \frac{3}{2}{a^2}\).
Trong không gian \(Oxyz\), cho \(\overrightarrow a = \left( {1;2; - 3} \right)\), \(\overrightarrow b = \left( {3;1;5} \right)\).
a) \(\overrightarrow a + \overrightarrow b = \left( {4;3;2} \right)\).
b) \(2\overrightarrow a - 3\overrightarrow b = \left( { - 7;1;21} \right)\).
c) \(\overrightarrow a .\overrightarrow b = 10\).
d) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{{\sqrt {10} }}{7}\).
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \(A(1;2;4),B(4; - 2;1),C(3;4;7)\)
a) Toạ độ trọng tâm \(G\) của tam giác \(ABC\) là \(G\left( {\frac{8}{3};\frac{4}{3};4} \right)\).
b) Toạ độ điểm \(D\) sao cho \(ABCD\) là hình bình hành là \(D\left( {0;8;10} \right)\).
c) Toạ độ điểm \(M\) thuộc đoạn \(AB\) sao cho \(MB = 2MA\) là \(M\left( {2;\frac{2}{3};3} \right)\).
d) \(\cos \widehat {BAC} = \frac{{11\sqrt 2 }}{{34}}\).
PHẦN III. CÂU HỎI TRẢ LỜI NGẮN
Trong không gian với hệ tọa độ \[Oxyz\], cho tam giác \(ABC\), biết \(A(1; - 2;0),B(2;1; - 1)\).Vectơ \(\overrightarrow {AB\,} = \left( {m\,;\,n\,;\,p} \right)\), khi đó hãy tìm \(T = m + n + p\).
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \[A\left( {1\,;\, - 1\,;\,2} \right)\] và \[B\left( { - 1\,;\,3\,;\,0} \right)\]. Trung điểm \(I\left( {a\,;\,b\,;\,c} \right)\) của đoạn thẳng \[AB\] có tổng \(T = a + b + c\).
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \(A\left( {2;1;1} \right)\) và \(B\left( { - 1;2;1} \right)\). Tọa độ điểm \[A'\left( {a\,;\,b\,;\,c} \right)\] là điểm đối xứng với \(A\) qua \(B\). Tìm \(a + b + c\).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[I\left( {2; - 3;4} \right)\]. Điểm đối xứng với điểm \[I\] qua trục \[Oy\] là \(I'\left( {a\,;\,b\,;\,c} \right)\). Tìm \(a + b + c\).
Trong không gian với hệ tọa độ \[Oxyz\], cho các điểm \(M\left( {0;1;2} \right)\),\(N\left( {2;0;1} \right)\),\(P\left( {0;0; - 1} \right)\),\(Q\left( {2;1;0} \right)\). Điểm nào trong 4 điểm đó thuộc mặt phẳng \(\left( {Oxy} \right)\). Hãy tính tổng \(T = 2a + 3b + 4c\) (Giả sử điểm thuộc mặt phẳng \(\left( {Oxy} \right)\)có dạng \(H\left( {a\,;\,b\,;\,c} \right)\))
Những căn lều gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác \(OAB.O'A'B'\) như trong Hình 2. Với hệ trục toạ độ \[Oxyz\] thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm \(A'\) và \(B'\) có tọa độ lần lượt là \(\left( {240;450;0} \right)\) và \(\left( {120;450;300} \right)\). Mỗi căn nhà gỗ có chiều dài là \(a{\rm{ cm}}\), chiều rộng là \(b\;{\rm{cm}}\), mỗi cạnh bên của mặt tiền có độ dài là \(c\;{\rm{cm}}\). Tính \(a + b + c\) (Làm tròn đến hàng đơn vị).