Đề kiểm tra Hệ trục tọa độ trong không gian (có lời giải) - Đề 2
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;\,1;\, - 2} \right)\) và \(B\left( {2;\,2;\,1} \right)\). Vectơ \(\overrightarrow {AB} \) có tọa độ là
\(\left( { - 1;\, - 1;\, - 3} \right)\).
\(\left( {3;\,1;\,1} \right)\).
\(\left( {1;\,1;\,3} \right)\).
\(\left( {3;\,3;\, - 1} \right)\).
Trong không gian \(Oxyz\), cho tam giác \(ABC\)có các điểm \(A\left( {1;0;3} \right)\), \(B\left( {2;3; - 4} \right)\), \(C\left( { - 3;1;2} \right)\). Tìm toạ độ điểm \(D\) sao cho tứ giác \(ABCD\) là hình bình hành.
\(\left( { - 4; - 2;9} \right)\).
\(\left( {4;2;9} \right)\).
\(\left( { - 2;4; - 5} \right)\).
\(\left( {6;2; - 3} \right)\).
Trong không gian \[Oxyz\], cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {1;\,0;\,1} \right)\), \(B\left( {2;\,1;\,2} \right)\), \(D\left( {1;\, - 1;\,1} \right)\). Tính tọa độ đỉnh \(C\) của hình hộp.
\(C\left( {4;\,6;\, - 5} \right)\).
\(C\left( {2;\,0;\,2} \right)\).
\(C\left( {3;5; - 6} \right)\).
\(C\left( {3;\,4;\, - 6} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\overrightarrow {OM} = \left( {1;5;2} \right)\], \[\overrightarrow {ON} = \left( {3;7; - 4} \right)\], \(K\left( { - 1;3;1} \right)\). Gọi \[P\] là điểm đối xứng với \[M\] qua \[N\]. Tìm tọa độ vectơ \[\overrightarrow {KP} \].
\(\overrightarrow {KP} = \left( {6;6; - 11} \right)\).
\[\overrightarrow {KP} = \left( {8;6; - 11} \right)\].
\[\overrightarrow {KP} = \left( {6;6; - 4} \right)\].
\[\overrightarrow {KP} = \left( {3;3; - 2} \right)\].
Trong hệ trục tọa độ \[Oxyz\], cho hai điểm là \[A\left( {1;3; - 1} \right)\], \[\overrightarrow {AB} = \left( {3; - 1;5} \right)\]. Tọa độ của \[\overrightarrow {OB} \] là
\[\overrightarrow {OB} = \left( { - 2;4; - 6} \right)\].
\[\overrightarrow {OB} = \left( {2; - 4;6} \right)\].
\[\overrightarrow {OB} = \left( { - 4; - 2; - 4} \right)\].
\[\overrightarrow {OB} = \left( {4;2;4} \right)\].
Trong không gian \[Oxyz\], cho điểm \[A\left( {1;2;3} \right)\]. Tìm tọa độ \[A'\] là điểm đối xứng với \[A\] qua trục \[Oy\].
\(A'\left( {1\,;\, - 2\,;\,3} \right)\).
\(A'\left( {1\,;\,2\,;\, - 3} \right)\).
\(A'\left( { - 1\,;\,2\,;\,3} \right)\).
\(A'\left( { - 1\,;\,2\,;\, - 3} \right)\)
Trong không gian \[Oxyz\], cho hình bình hành \[ABCD\] tâm \[I\] có tọa độ các đỉnh \[B\left( {3;\,1;\,0} \right)\], \[D\left( {0;\,4;\, - 6} \right)\]. Tìm tọa độ điểm \[I\].
\[I\left( {\frac{3}{2};\,\frac{5}{2};\, - 3} \right)\].
\[I\left( {3;\,5;\, - 6} \right)\].
\[I\left( { - \frac{3}{2};\,\frac{3}{2};\, - 3} \right)\].
\[I\left( { - 3;\,5;\, - 6} \right)\].
Trong không gian \[Oxyz\], cho điểm \[M\] thoả \[\overrightarrow {OM} = 3\,\overrightarrow i + 5\overrightarrow j - 7\overrightarrow k \]. Tìm tọa độ điểm đối xứng \[M'\]của \[M\]qua mặt phẳng \[\left( {Oxz} \right)\].
\[M'\left( { - 3;\, - 5;\,7} \right)\].
\[M'\left( {3;\,5;\, - 7} \right)\].
\[M'\left( { - 3;\,5;\,7} \right)\].
\[M'\left( {3;\, - 5;\, - 7} \right)\].
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\)có điểm \(A\) trùng với gốc tọa độ \(O\), điểm \(B\) nằm trên tia \(Ox\), điểm \(D\)nằm trên tia \(Oy\), điểm \(A'\)nằm trên tia \(Oz\).Biết \(AB = 2,\,AD = 4,\,AA' = 3\). Gọi tọa độ của \(C'\) là \(\left( {a;\,b;\,c} \right)\) khi đó biểu thức \(a + b - c\) có giá trị là.
\( - 4\).
\(9\).
\(3\).
\(6\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có điểm \(B\) trùng với gốc tọa độ \(O\)và tọa độ các điểm \(A\left( {3;0;0} \right)\), \(D\left( {3;1;0} \right)\), \(B'\left( {0;0;5} \right)\). Gọi tọa độ \(C'\left( {m;n;p} \right)\). Tính \({m^2} + {n^2} + {p^2}\)
\(26\).
\(9\).
\(16\).
\(37\).
Trong không gian với hệ trục toạ độ \(Oxyz\), cho \(\overrightarrow {\,a\,} = \left( {2;\,3;\,1} \right)\), \(\overrightarrow {\,b\,} = \left( { - 1;\,5;\,2} \right)\), \(\overrightarrow {\,c\,} = \left( {4;\, - 1;\,3} \right)\) và \(\overrightarrow {\,x\,} = \left( { - 3;\,22;\,5} \right)\). Đẳng thức nào đúng trong các đẳng thức sau?
\(\overrightarrow {\,x\,} = 2\overrightarrow {\,a\,} - 3\overrightarrow {\,b\,} - \overrightarrow {\,c\,} \)
\(\overrightarrow {\,x\,} = - 2\overrightarrow {\,a\,} + 3\overrightarrow {\,b\,} + \overrightarrow {\,c\,} \)
\(\overrightarrow {\,x\,} = 2\overrightarrow {\,a\,} + 3\overrightarrow {\,b\,} - \overrightarrow {\,c\,} \)
\(\overrightarrow {\,x\,} = 2\overrightarrow {\,a\,} - 3\overrightarrow {\,b\,} + \overrightarrow {\,c\,} \)
Trong không gian với hệ tọa độ \(Oxyz\)cho hình hộp \[ABCD.A'B'C'D'\]. Biết \[A\left( {2;\,4;\,0} \right)\], \[B\left( {4;\,0;\,0} \right)\], \[C\left( { - 1;\,4;\, - 7} \right)\]và \[D'\left( {6;\,8;\,10} \right)\]. Tọa độ điểm \[B'\] là
\[B'\left( {8;\,4;\,10} \right)\]
\[B'\left( {6;\,12;\,0} \right)\]
\[B'\left( {10;\,8;\,6} \right)\]
\[B'\left( {13;\,0;\,17} \right)\]
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian \(Oxyz\), cho ba vectơ \(\overrightarrow u = \left( {3;1; - 2} \right),{\rm{ }}\overrightarrow v = \left( {1; - 1;1} \right),{\rm{ }}\)\(\overrightarrow w = \left( { - 1; - 3;4} \right)\).
a) \(\overrightarrow u + \overrightarrow v = \left( {4;0; - 2} \right)\).
b) \(\overrightarrow u \bot \overrightarrow v \).
c) Hai vectơ \(\overrightarrow u - 2\overrightarrow v \) và \(\overrightarrow w \) cùng hướng.
d) \(\left| {\overrightarrow u - \overrightarrow v + 2\overrightarrow w } \right| = \sqrt {41} \).
Trong không gian \(Oxyz\), cho tam giác \(ABC\) với \(A\left( {1;0; - 2} \right),\;B\left( { - 2;3;4} \right),\,C\left( {4; - 6;1} \right)\).
a) Tọa độ trọng tâm G của tam giác là \(\left( {1; - 1;1} \right)\).
b) \(\overrightarrow {AB} = \left( {3; - 3;6} \right),\,{\rm{ }}\overrightarrow {AC} = \left( { - 3;6; - 3} \right).\)
c) Tam giác \(ABC\)là tam giác cân .
d) Nếu \(ABDC\) là hình bình hành thì tọa độ điểm D là \(\left( {7; - 9; - 5} \right)\).
Trong không gian \(Oxyz\), cho hình lập phương \(ABCD.A'B'C'D'\) có \(A\left( {0;0;0} \right)\), \(B\left( {4;0;0} \right)\), \(D\left( {0;4;0} \right)\). Gọi \(E\) là trung điểm của \(AB\) và \(F\) là điểm nằm trên tia đối của tia \(AD\) sao cho \[AF = 1\].
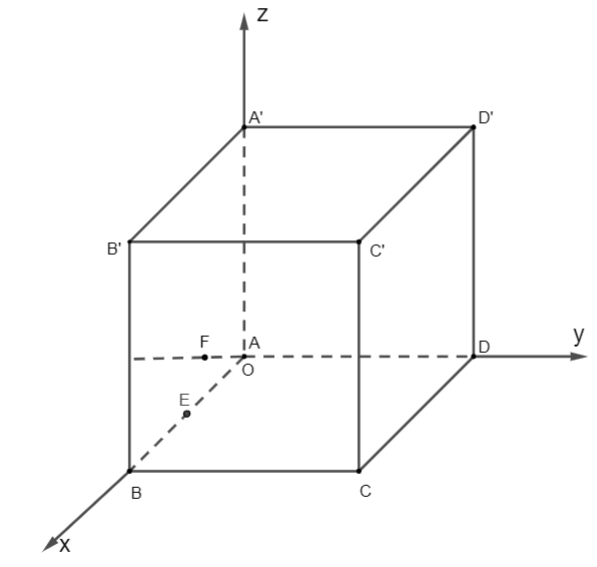
a) Tọa độ của điểm \(C\)là \(C\left( {0;4;4} \right)\).
b) Tọa độ của điểm \(B'\) là \(B'\left( {4;0;4} \right)\).
c) Tọa độ của điểm \(E\) là \(\left( {2;2;0} \right)\).
d) Tọa độ của điểm \(F\) là \(\left( {0;1;0} \right)\).
Trong không gian \(Oxyz\), cho vecto và .
a) Tọa độ của vecto \(\overrightarrow {i\,} \) là \(\left( {0;1;0} \right)\).
b) Tọa độ của vecto \(\overrightarrow {OA\,} \) là \(\left( {x\,;y\,;z} \right)\).
c) Tọa độ của điểm \(B\) là \(\left( {x';y';z'} \right)\).
d) Nếu \(\overrightarrow {OA\,} = \overrightarrow {OB\,} \) thì \(x = x',\,y = y',\,z = z'\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 17 đến câu 22.
Trong không gian\(Oxyz\), cho hai điểm \(A\left( {2;0; - 1} \right)\), \(B\left( {1;1;3} \right)\). Xác định tọa độ vectơ \(\overrightarrow {DC} \) sao cho tứ giác \(ABCD\) là hình bình hành.
Trong không gian\(Oxyz\), cho \(\overrightarrow {OC} = 2\overrightarrow i - \overrightarrow k \). Xác định tọa độ hình chiếu vuông góc của điểm \(C\) trên trục \[Ox\].
Trong không gian \(Oxyz\) , cho mặt phẳng hình hộp \(OABC.O'A'B'C'\) có \(A\left( {2\,;\,1\,;\, - 1} \right)\), \(B\left( {0\,;\,3\,;1} \right)\) và \(C'\left( {2\,;\, - 3\,;\,5} \right)\). Xác định toạ độ điểm \(O'\).
Trong không gian với hệ trục toạ độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm \(A\left( {600\,;\,400\,;\,8} \right)\) đến điểm \(B\left( {800\,;\,500\,;\,10} \right)\) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo là gì?
Trong không gian \(Oxyz\), cho điểm \(A\left( { - 3;0;0} \right)\), \(B\left( {0; - 4;0} \right)\). Gọi \(I\), \(J\) lần lượt là tâm đường tròn nội tiếp và ngoại tiếp của tam giác \(OAB\). Tính độ dài đoạn thẳng \(IJ\).
Một công ty viễn thông đang lên kế hoạch xây dựng một tháp viễn thông tại một thành phố để cung cấp dịch dụ tốt hơn. Công ty cần xác định vị trí của tháp sao cho có thể phủ sóng hiệu quả đến ba toà nhà quan trọng trong thành phố. Giả sử các toà nhà này được đặt tại các vị trí có toạ độ như sau:
Toà nhà \(A\left( {0;0;0} \right)\)
Toà nhà \(B\left( {6;0;0} \right)\)
Toà nhà \(C\left( {3;\sqrt 3 ;2\sqrt 6 } \right)\)
Tháp viễn thông phải đặt ở vị trí sao cho tổng khoảng cách từ tháp đến 3 toà nhà là nhỏ nhất. Khi đó tổng khoảng cách từ vị trí của tháp đến ba toà nhà bằng bao nhiêu?